1,题目
输入一个十进制的数,输出
(1)、给定n,求出从1到n的所有整数中1的个数。(暂用用f(n)表示)
(2)、求满足n=f(n)的最小整数(1除外)。
假如需要求的N=23106,那么计算过程如下:
万位为1:1 0000--1 9999 共计10000个
千位为1: 0 1 000--2 1 999 共计3*1000 = 3000,其中3表示万位可以填0,1,2三种情况,1000表示后面三位有000-999共1000种可能,所以总共可有3000种可能
百位为1:这里的可能情况并不是:00 1 00--23 1 99,因为最大只能到23106,所以我们可以把总和分为2部分:
00 1 00--221 99:共计23*100种,其中23表示万千位可以取00-22,23种可能,100表示十个位可以取00-99,100中可能。
23 1 00--231 06:共计7种,即万千位都固定,只有23一种情况,十个位可以取00-56,共57种可能
所以百位为1的数字数目,有2300+7 = 2307种;
十位为1:000 1 0--230 1 9 共计231*10=2310种,其中231表示万千百位可以取000-231,232种可能,而10表示个位可以去0-9十种可能。
因为以23110>23106,所以万千百位=231,且十位=1的数字数目为0
个位为1:0000 1--2310 1 共计2311*1种
所以总计数目:10000+3000+2307+2310+2311 = 19928种可能。
所以我们只需要对数字位数上的1进行分解计算即可。
下面以12为例写一个简单代码
代码如下:
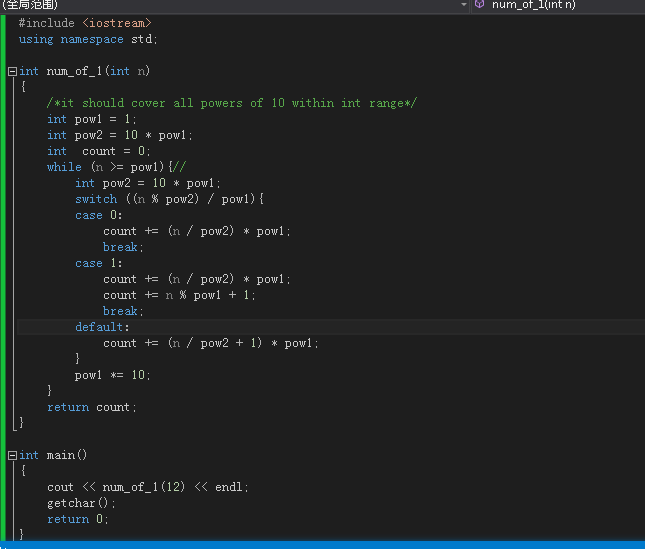
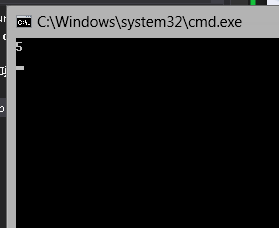
可以看到最后的计算结果为:
总结:重要的还是思想,就像大道至简中说的代码只是“愚公移山”,相信以后能和计算机更好的交流。