| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 25950 | Accepted: 8853 |
Description
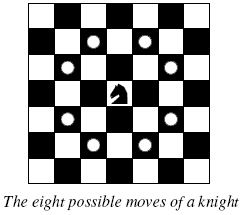Background The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
Sample Input
3 1 1 2 3 4 3
Sample Output
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4
题意：给出p和q,p代表行数（1，2,3....）,q代表列数（A,B,C....）,要求输出骑士从任意一点出发经过所有点的路径，必须按字典序输出；路径不存在输出impossible；
思路：与dfs模板不同的是路径按字典序输出，所以dfs的顺序就不是随意的了，必须按dir[8][2] = {{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}}的顺序；
而且起点必须是A1,这样得出的路径字典序才最小；
1 #include<iostream> 2 #include<stdio.h> 3 #include<string.h> 4 using namespace std; 5 6 struct node 7 { 8 int row; 9 int col; 10 }way[30];//记录所走路径的行和列 11 12 int p,q; 13 bool vis['Z'+1][27]; 14 int dir[8][2] = {{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}}; 15 16 bool DFS(struct node* way,int i,int j,int step) 17 { 18 vis[i][j]=true; 19 way[step].row=i; 20 way[step].col=j; 21 if(step==way[0].row) 22 return true; 23 24 for(int k=0; k<8; k++)//向八个方向走 25 { 26 int ii = i+dir[k][0]; 27 int jj = j+dir[k][1]; 28 if(!vis[ii][jj] && ii>=1 && ii<=p && jj>=1 && jj<=q) 29 if(DFS(way,ii,jj,step+1)) 30 return true; 31 } 32 33 vis[i][j]=false; 34 return false; 35 } 36 37 int main() 38 { 39 int test; 40 scanf("%d",&test); 41 for(int t = 1; t <= test; t++) 42 { 43 memset(vis,false,sizeof(vis)); 44 scanf("%d %d",&p,&q); 45 46 way[0].row =p*q; 47 48 if(DFS(way,1,1,1)) 49 { 50 cout<<"Scenario #"<<t<<':'<<endl; 51 52 for(int k=1; k<=way[0].row; k++) 53 cout<<(char)(way[k].col-1+'A')<<way[k].row; 54 cout<<endl<<endl; 55 56 } 57 58 else 59 { 60 cout<<"Scenario #"<<t<<':'<<endl; 61 cout<<"impossible"<<endl<<endl; 62 } 63 } 64 return 0; 65 }