题解 洛谷 P3369 【【模板】普通平衡树】

指针Splay题解

前言

Splay是像我这样的小蒟蒻一开始学的平衡树。

虽然Splay常数不小，但是功能十分全面，既可以当区间树也可以当平衡树(当然这两者不可兼顾)

看到题解里一堆dalao写数组,但是Splay本来是应该用指针实现的（据说这样常数会小很多）,于是蒟蒻就开始写起了指针Splay。。。

出人意料，数组Splay我一遍A,指针我居然调试了将近一年（真事）我果然太蒟了。似乎明白了大家为什么都不用指针。

但是，从一遍遍的调试之间，我还是学到了不少东西，比如如何增加代码的可调试性，如何考虑到方方面面以防止RE。这可能也是一种进步。最后发现，其实指针Splay也挺好(nan)打，更重要的是，指针也更方便理解。

为了希望大家少走点弯路.带大家入调试大坑本蒟蒻觉得有必要写一份详细的指针Splay题解.

大部分资料来源于网络。

Spaly最快了233

正文

(本文假设大家都对二叉查找树有基本理解，不再赘述一些常识.网上的讲的比我好多了)（本文默认节点左小右大）

一些前置函数

获取节点的大小

inline unsigned int size(tree x){return x?x->size:0;}/*防止x为空导致访问NULL的信息(RE)*/

维护节点大小

inline void pushup(tree x){x->size=size(x->ch[0])+size(x->ch[1])+x->cnt;}//一个节点的大小等于它的左子树的大小+右子树大小+本身的个数(可以有重复)

获取节点是它父亲的那个儿子

inline bool wson(tree son,tree par)//0为左儿子，一为右儿子
{
	if(!par)return 0;//父亲为空防止RE
	return par->ch[1]==son;
}

建立父子关系

inline void buildfather(tree son,tree par,bool which)//0表示变为左儿子，1表示变为右儿子
{
	if(son)son->par=par;
	if(par)par->ch[which]=son;
	else root=son;//如果父亲为空，自然其为根。
}

旋转操作

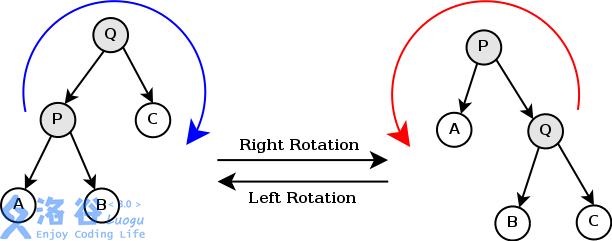
旋转操作是Splay Tree的核心操作
它通过旋转在不破坏BST的性质的情况下，调整树的结构。

图中可以看出C>Q>B>P>A.

我们的目标是将P转到Q的位置

直接交换肯定不行，这破坏了BST的性质。

事实上，我们可以看出，A与C的位置一定是固定的。

P,Q是我们需要交换的节点，所以我们可以通过对B进行换位来保证BST的性质不被破坏。以右旋为例。右图仍然有C>Q>B>P>A.

这样就成功实现了上旋的操作

个人习惯将左右旋转写在一个函数中

inline void rotate(tree x)
{
	tree p=x->par,g=p->par;//这里导致我调试了一年。
	bool r=wson(x,p);//本来我仿照的数组的题解，将wson(x)表示x为它的父亲的哪一个孩子。但是旋转过程中父子关系产生了变化，于是就必须提前记录好par,与grandpar.
	buildfather(x,g,wson(p,g));//将x提到p的位置。就必须将g的儿子（p）的位置变成x。所以这里用了wson(p,g).
	buildfather(x->ch[!r],p,r);//x->ch[!r]即为图中的B.
	buildfather(p,x,!r);//将p设为x的儿子，在原来B的位置上
	pushup(p);//这里为什么不需要pushup(x)，Splay函数会给出相关解释
}

Splay操作

Splay是SplayTree的核心操作(废话)。
它通过rotate，单旋与双旋来维护Splay Tree的深度。
如果不理解双旋(或者是Spaly教的忠实信奉着)可以参考网上资料

这里因为是主要讲解指针，所以不再赘述。

inline void Splay(tree x,tree y)//将x转到y的下方
{
	while(x->par!=y)//直到x的父亲是y.
	{
		tree p=x->par,g=p->par;//同rotate及时预处理好p与g.(虽然这里没有必要)
		if(x->par->par!=y)wson(x,p)^wson(p,g)?rotate(x):rotate(p);//如果成一条链就先转p,反之转两次x
        rotate(x);
	}
	pushup(x);//填坑，因为你每一次rotate都将x向上转，那么你的x的size一定会一直改变，所以在rotate里面pushup(x)没有意义。只需要在最后pushup(x)即可。
}

Insert操作

建树时，当然可以预先读入数据构建完美的Splay.
这里只给出Insert.毕竟复杂度也没差多少

inline void insert(int val)
{
	if(!root)//特判root为空情况
	{
		root=new node(val,NULL);
		return;
	}
	for(tree x=root;x;x=x->ch[val>=x->val])//从root向下插入，每次判断应当走哪边
	{
		if(x->val==val)//如果已经有这个元素了。则cnt++.
		{
			x->cnt++;
			Splay(x,NULL);//维护Splay深度
			return;
		}
		if(!x->ch[val>=x->val])//如果到了空，也就是没有这个节点
		{
			x->ch[val>=x->val]=new node(val,x);//新建一个节点，C++的new和delete较慢，这里为了友好一点就不用内存池了233.
			Splay(x->ch[val>=x->val],NULL);
			return;
		}
	}
}

Find操作

同普通BST

inline void find(int val)
{
	tree x=root;
	while(x/*root为空*/&&x->ch[val>x->val]/*这里因为要精确查找所以将>=分开成了>与=两种情况*/&&val!=x->val/*找到了*/)x=x->ch[val>x->val];
	if(x)Splay(x,NULL);//记得在每个操作都要Splay
}

Delete操作

这是一个比较复杂的点.

你当然也可以将前驱旋转到根，后继旋转到右子树，然后直接删除右子树的左子树。但这样需要提前插入INF与-INF(或特判)，个人认为比较容易出错，毕竟你的Splay里多了两个节点，findkth(k),需要将k++(INF永远比你大)）

详见注释

inline int del(int val)
{
	find(val);//将值为val的点转到根 
	if(root->val!=val)return;//找不到
	tree x=root;
	if(x->cnt>1)x->cnt--;//多于一个。 
	else 
	if(!x-ch[0])//有一子树为空 
	{
		root=x->ch[1];//root转移到另外一边 
		if(root)root->par=NULL;//防止RE. 
		delete x;//回收x 
	}
	else//两子树都非空 
	{
		tree k=x->ch[0];//找到左子树中最大的一个 
		while(k->ch[1])k=k->ch[1];
		Splay(k,x);//将他旋转到左子树的根上 
		root=k,root->par=NULL;//这个时候左子树的右子树肯定为空 
		buildfather(x->ch[1],root,1);//再将右子树转移到左子树的右子树 
		delete x;//回收x 
	}
}

这里理解可能有些难度，可以考虑手玩一下。

kth操作

这个不难，但是一定要画出图，不能想当然!

inline int findkth(int k)
{
	tree x=root;
	assert(size(x)>=k);//元素个数一定要至少有k个,且没有第0大 
    assert(k);//你可以选择无视这两句话
	while(x)
	{
		if(size(x->ch[0])+x->cnt>=k&&size(x->ch[0])<k)return x->val;//如果你左子树的大小加上你的个数>=k并且你左子树的大小<k那么你就是第k大
		if(size(x->ch[0])>=k)x->ch[0];//如果左子树大小
		else k-=size(x->ch[0])+x->cnt,x=x->ch[1]; //
	}
	return -2147483647;//出现未知错误 (树的构建可能出现问题)（如果你其他地方正确，这里并不会有用）
}	

前驱与后继(pre&nxt)操作

前驱就是比你小的最大的一个
后继就是比你大的最小的一个
所以前驱就是左子树的最右一个
后继同理
这里只对于前驱做出说明

inline int pre(int val)
{
	insert(val);//插入val,它会被转到root
	tree x=x->root->ch[0];
	while(x->ch[1])x=x->ch[1];//找到比val小的最大的数
	del(val);//再删掉
	return x->val;
}
inline int nxt(int val)
{
	insert(val);
	tree x=x->root->ch[1];
	while(x->ch[0])x=x->ch[0];
	del(val);
	return x->val;
}

完整代码

#include<bits/stdc++.h>
using namespace std;
#define IL inline
#define RG register
#define gi getint()
#define pi(k) putint(k)
#define gc getchar()
#define File(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout)
IL int getint()
{
    RG int xi=0;
    RG char ch=gc;
    bool f=0;
    while(ch<'0'|ch>'9')ch=='-'?f=1:f,ch=gc;
    while(ch>='0'&ch<='9')xi=(xi<<1)+(xi<<3)+ch-48,ch=gc;
    return f?-xi:xi;
}
IL void putint(int k)
{
    if(k<0)k=-k,putchar('-');
    if(k>=10)putint(k/10);
    putchar(k%10+'0');
}
struct SplayTree{
	struct node;
	typedef node* tree;
	struct node{
		tree ch[2],par;
		int size,val,cnt;
		node(int value,tree fa)
		{
			val=value,par=fa;
			size=1,cnt=1;
			ch[0]=ch[1]=NULL; 
		}
	}*root;
	SplayTree(){root=NULL;}
	inline int size(tree x){return x?x->size:0;}
//	#define size(x) (x?x->size:0)
	inline void pushup(tree x){if(x)x->size=size(x->ch[0])+size(x->ch[1])+x->cnt;}
	inline void buildfather(tree son,tree par,bool which)
	{
		if(son)son->par=par;
		if(par)par->ch[which]=son;
		else root=son;
	}
	inline bool wson(tree son,tree par)
	{
		if(!par)return 0;
		return par->ch[1]==son;
	}
	inline void rotate(tree x)
	{
		tree p=x->par,g=p->par;
		bool r=wson(x,p);
		buildfather(x,g,wson(p,g));
		buildfather(x->ch[!r],p,r);
		buildfather(p,x,!r);
		pushup(p);
	}
	inline void Splay(tree x,tree y)
	{
		while(x->par!=y)
		{
			tree p=x->par,g=p->par;
			if(x->par->par!=y)wson(x,p)^wson(p,g)?rotate(x):rotate(p);
			rotate(x);
		}
		pushup(x);
	}
	inline void insert(int val)
	{
		if(!root)
		{
			root=new node(val,NULL);
			return;
		}
		for(tree x=root;x;x=x->ch[val>=x->val])
		{
			if(x->val==val)
			{
				x->cnt++;
				Splay(x,NULL);
				return;
			}
			if(!x->ch[val>=x->val])
			{
				x->ch[val>=x->val]=new node(val,x);
				Splay(x->ch[val>=x->val],NULL);
				return;
			}
		}
	}
	inline void find(int val)
	{
		tree x=root;
		while(x&&x->ch[val>x->val]&&val!=x->val)x=x->ch[val>x->val];
		if(x)Splay(x,NULL);
	}
	inline int findkth(int k)
	{
		tree x=root;
		assert(size(x)>=k);
        assert(k);
		while(x)
		{
			if(size(x->ch[0])+x->cnt>=k&&size(x->ch[0])<k)return x->val;
			if(size(x->ch[0])>=k)x=x->ch[0];
			else k-=size(x->ch[0])+x->cnt,x=x->ch[1]; 
		}
		return -2147483647;
	}
	inline void del(int val)
	{
		find(val);
		if(root->val!=val)return;
		tree x=root;
		if(x->cnt>1)x->cnt--;
		else 
		if(!x->ch[0])
		{
			root=x->ch[1];
			if(root)root->par=NULL; 
			delete x;
		}
		else
		{
			tree k=x->ch[0];
			while(k->ch[1])k=k->ch[1];
			Splay(k,x);
			root=k,root->par=NULL;
			buildfather(x->ch[1],root,1); 
			delete x;
		}
	}
	inline int pre(int val)
	{
		insert(val);
		tree x=root->ch[0];
		while(x->ch[1])x=x->ch[1];
		del(val);
		return x->val;
	}
	inline int nxt(int val)
	{
		insert(val);
		tree x=root->ch[1];
		while(x->ch[0])x=x->ch[0];
		del(val);
		return x->val;
	}
}bt; 
int main(void)
{
	int n=gi;
    int a;
    for(RG int i=1; i<=n; i++)
        switch(gi)
        {
            case 1:
                a=gi;
                bt.insert(a);
                break;
            case 2:
                a=gi;
                bt.del(a);
                break;
            case 3:
                a=gi;
                bt.find(a);
                printf("%d
",bt.size(bt.root->ch[0])+1);//这能理解吗
                break;
            case 4:
                a=gi;
                printf("%d
",bt.findkth(a));
                break;
            case 5:
                a=gi;
                printf("%d
",bt.pre(a));
                break;
            case 6:
                a=gi;
                printf("%d
",bt.nxt(a));
                break;
        }
    return 0;
}