$cf$ 自闭了,打 $abc$ 散散心
...这个有什么好讲的吗,题目看懂就会做了

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } int a,b; int main() { a=read(),b=read(); if(a>9||b>9||a<1||b<1) { printf("-1 "); return 0; } printf("%d ",a*b); return 0; }
预处理一下哪些数可以被表示然后查表即可

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=233; bool vis[N]; int main() { for(int i=1;i<=9;i++) for(int j=1;j<=9;j++) vis[i*j]=1; int a=read(); if(vis[a]) printf("Yes "); else printf("No "); return 0; }
C - Walk on Multiplication Table
根号枚举一下因数,设因数为 $x$ ,那么看看走到 $(x,n/x)$ 是不是比较短的路径即可

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; inline ll read() { ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } ll n,ans; int main() { n=read(); int t=sqrt(n); ans=n-1; for(int i=2;i<=t;i++) { if(n%i) continue; ans=min(ans,n/i+i-2); } printf("%lld ",ans); return 0; }
对我这个数学不好的人来说很不友好啊...
显然二分一下倾斜角看看水是否会倒出来
首先可以把 $x$ 除以 $a$ ,然后就变成平面的问题
然后要特判一下内部是梯形还是三角形就做完了,要注意一下细节,别和我一样把精度设到 $1e-18$ 或者 $-1e18$ ,$ ext{2333333}$
放张图比较好理解吧:
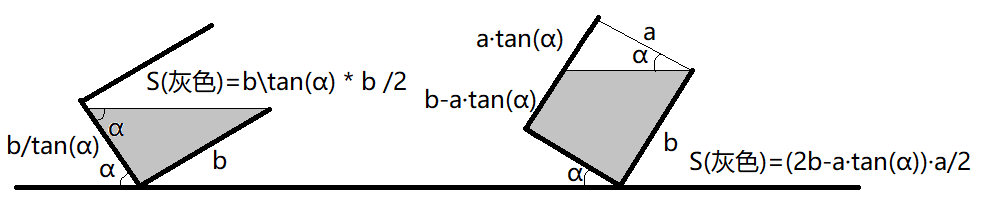

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; typedef long double ldb; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const ldb pi=acos(-1.0),eps=1e-12; ldb a,b,x,ans; inline bool check(ldb alp) { if(a*tan(alp)>=b) { ldb y=b/tan(alp); return y*b/2<=x; } ldb t=b-a*tan(alp); return (t+b)*a/2<=x; } int main() { cin>>a>>b>>x; x/=a; ldb L=eps,R=pi/2-eps; while(fabsl(R-L)>eps) { ldb mid=(L+R)/2; if(check(mid)) R=mid,ans=mid; else L=mid; } printf("%.12Lf ",ans/pi*180); return 0; }
首先容易想到最大的 $A$ 和最小的 $F$ 匹配,次大的和次小的匹配...这样匹配下去
然后考虑如何减一些 $A$ ,显然可以二分答案,那么 $check$ 长这样:
inline bool check(ll p)//二分的答案p { ll now=K; for(int i=1;i<=n;i++) { // af<=p , a<=p/f if(p/F[i]>=A[i]) continue; ll t=A[i]-p/F[i]; if(t>now) return 0; now-=t; } return 1; }
分析完代码发现,为了最优一定要 $A$ 从小到大对应匹配 $F$ 从大到小,一种证明大概是这样的:
首先可以发现,对于二分的答案 $p$ ,它需要的 $K$ 为 $sum_{i=1}^{n}max(A_i-left lfloor frac{p}{F_i} ight floor,0)$
那么式子相当于 $sum_{i=1}^{n}A_i-sum_{i=1}^{n}left lfloor frac{p}{F_i} ight floor+sum_{i=1}^{n}[A_i<left lfloor frac{p}{F_i} ight floor](left lfloor frac{p}{F_i} ight floor-A_i)$
发现如果某种匹配能让最后一项求和尽量小,那么即为最优的
然后问题就变成了给长度为 $n$ 的序列 $A,B$ ,求一种匹配使 $sum_{i=1}^{n}[A_i<B_i](B_i-A_i)$ 最小
首先对于最大的 $B_x$ ,如果 $A_i,A_j$ 都大于 $B_x$ ,那么 $i,j$ 选那个没影响,如果 $A_i<B<A_j$ 显然要让 $A_j$ 去和 $B_x$ 匹配
因为如果让 $A_i$ 和 $B_x$ 匹配,首先产生的代价一定大于 $A_i$ 和 $B_y,y eq x$ 匹配的代价,然后 $A_j$ 不管和谁匹配代价都为 $0$,那么综合一下还是要让 $A_j$ 去匹配 $B_x$
如果 $A_i<A_j<B$ ,那么如果 $A_i$ 和 $B_x$ 匹配并且 $A_j$ 和 $B_y$ 匹配,如果 $A_j<B_y$ 那么交换 $i,j$ 对答案没影响
但是如果 $A_j>B_y$ ,自己写一下式子会发现代价大于等于 $A_j$ 和 $B_x$ 匹配,$A_i$ 和 $B_y$ 匹配的代价(这里要再分 $B_y$ 和 $A_i$ 之间的关系讨论)
所以综上,$A$ 中最大的和 $B$ 中最大的匹配,次大的和次大的匹配,这样下去一定不会劣于其他方案
回到原来的问题,因为 $F$ 变成了分母,所以要 $F$ 最小的和 $A$ 最大的匹配

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> using namespace std; typedef long long ll; inline ll read() { ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=2e5+7; const ll INF=1e12; ll n,m,A[N],F[N]; inline bool check(ll p) { ll now=m; for(int i=1;i<=n;i++) { // af<=p , a<=p/f if(p/F[i]>=A[i]) continue; ll t=A[i]-p/F[i]; if(t>now) return 0; now-=t; } return 1; } int main() { n=read(),m=read(); for(int i=1;i<=n;i++) A[i]=read(); for(int i=1;i<=n;i++) F[i]=read(); sort(A+1,A+n+1); sort(F+1,F+n+1); reverse(F+1,F+n+1); ll L=0,R=INF,ans=0; while(L<=R) { ll mid=L+R>>1; if(check(mid)) R=mid-1,ans=mid; else L=mid+1; } printf("%lld ",ans); return 0; }
一开始显然会考虑枚举断边然后 $dp$ 一下算代价
设 $f[x]$ 表示从 $x$ 出发最终到达 $n$ 的期望步数,那么转移显然
但是枚举断边复杂度为 $m$,总复杂度为 $m(n+m)$ ,不太行
考虑枚举点,对于某个点 $u$ ,它有若干的出边 $(u,v_i)$
考虑断掉哪条从 $u$ 出发的边是最优的,显然是 $f[v_i]$ 最大的那个,所以只要考虑断最大的那个即可
那么枚举点的复杂度为 $n$ ,总复杂度为 $n(n+m)$,记得如果某个点没法走到 $n$ ,那么期望步数为 $INF$

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<vector> using namespace std; typedef long long ll; typedef double db; inline int read() { int x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*f; } const int N=607,INF=1e9; int n,m,a[N*N],b[N*N]; vector <int> V[N]; db f[N],ans; inline db calc(int p) { for(int i=1;i<=n;i++) f[i]=0; f[n]=0; for(int i=n-1;i>=1;i--) { int len=V[i].size(); if(p==i&&len==1) { f[i]=INF; continue; } db t=1.0/(len-(p==i)),mx=0; for(int j=0;j<len;j++) { int v=V[i][j]; mx=max(mx,(f[v]+1)*t); f[i]+=(f[v]+1)*t; } if(p==i) f[i]-=mx; } return f[1]; } int main() { n=read(),m=read(); for(int i=1;i<=m;i++) { a[i]=read(),b[i]=read(); V[a[i]].push_back(b[i]); } ans=calc(0); for(int i=1;i<=n;i++) ans=min(ans,calc(i)); printf("%.9lf ",ans); return 0; }
