题目描述:
给定一个字符串
求出该字符串最多由几个相同的子串连接构成
字符串长度 n<=1000000
hash or KMP
hash的话就枚举长度,暴力判断
复杂度约为O(n log n)
主要是KMP怎么搞
先想想如果该字符串是由一些相同的子串构成,如abcabcabcabc
那么fail数组就为 0 0 0 0 1 2 3 4 5 6 7 8 9(从fail[0] 到 fail[12])
然后可以发现 n - fail[n] 就是子串的长度
那要怎么证明呢
设子串长度为 l,那么从 0~fail[n] -1 的串肯定与 l ~ n-1 的串相同
如图
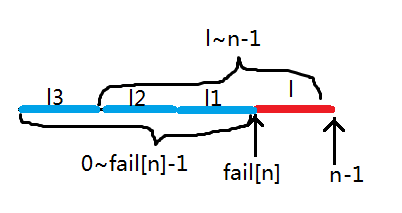
所以字符串 l = l1,l1 = l2,l2 = l3
证明大概就是这样...
但是如果 l 不整除 n,那就不存在这种子串了
因为如果存在这种子串,那么 l 一定整除 n(自行脑补)
所以就可以用KMP了,代码很简单的
复杂度O(n)
#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int fail[10000007]; char ch[10000007]; int main() { scanf("%s",ch); while(ch[0]!='.') { memset(fail,0,sizeof(fail)); int len=strlen(ch); int x=0; for(int i=1;i<len;i++) { while(ch[i]!=ch[x]&&x) x=fail[x]; fail[i+1]= ch[i]==ch[x] ? ++x : 0; } printf("%d ",len%(len-fail[len]) ? 1 : len/(len-fail[len]) ); scanf("%s",ch); } return 0; }