bzoj1491 [NOI2007]社交网络

[NOI2007]社交网络

Time Limit: 10 Sec Memory Limit: 64 MB

Description

在社交网络（socialnetwork）的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。
在一个社交圈子里有n个人，人与人之间有不同程度的关系。我们将这个关系网络对应到一个n个结点的无向图上，
两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值c，c越小，表示两个人
之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度，注意到最短路
径上的其他结点为s和t的联系提供了某种便利，即这些结点对于s和t之间的联系有一定的重要程度。我们可以通过
统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点A和B之间可能会有
多条最短路径。我们修改重要程度的定义如下：令Cs,t表示从s到t的不同的最短路的数目，Cs,t(v)表示经过v从s
到t的最短路的数目；则定义

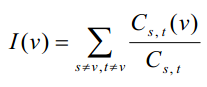
为结点v在社交网络中的重要程度。为了使I(v)和Cs,t(v)有意义，我们规定需要处理的社交网络都是连通的无向图
，即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图，请你求出每
一个结点的重要程度。

Input

输入第一行有两个整数n和m，表示社交网络中结点和无向边的数目。在无向图中，我们将所有结点从1到n进行编号
。接下来m行，每行用三个整数a，b，c描述一条连接结点a和b，权值为c的无向边。注意任意两个结点之间最多有
一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。n≤100；m≤4500
，任意一条边的权值 c 是正整数，满足：1≤c≤1000。所有数据中保证给出的无向图连通，且任意两个结点之间
的最短路径数目不超过 10^10

Output

输出包括n行，每行一个实数，精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。

Sample Input

4 4

1 2 1

2 3 1

3 4 1

4 1 1

Sample Output

1.000

1.000

1.000

1.000

HINT

社交网络如下图所示。

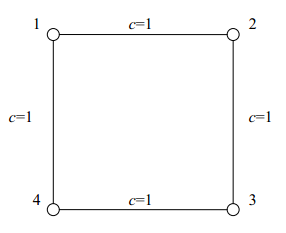
对于 1 号结点而言，只有 2 号到 4 号结点和 4 号到 2 号结点的最短路经过 1 号结点，而 2 号结点和 4 号结

点之间的最短路又有 2 条。因而根据定义，1 号结点的重要程度计算为 1/2 + 1/2 = 1 。由于图的对称性，其他

三个结点的重要程度也都是 1 。




最短路瞎计数？？？

#include<bits/stdc++.h>
#define N 105
using namespace std;
struct lpl{
	int to, dis;
	inline bool operator < (const lpl &A)const{
		return dis > A.dis;
	}
};
int n, m;
int dis[N][N];
long long md[N][N], data[N];
bool vis[N];
vector<lpl> point[N];
priority_queue<lpl> q;

inline void putit(){
	lpl lin; memset(dis, 0x3f, sizeof(dis));
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; ++i) dis[i][i] = 0;
	for(int a, b, i = 1; i <= m; ++i){
		scanf("%d%d%d", &a, &b, &lin.dis);
		lin.to = b; point[a].push_back(lin);
		lin.to = a; point[b].push_back(lin);
		dis[a][b] = dis[b][a] = min(dis[a][b], lin.dis);
	}	
//	for(int i = 1; i <= n; ++i)
//		for(int j = 1; j <= n; ++j)
//			printf("dis[%d][%d] = %d
", i, j, dis[i][j]);
}

inline void floyd(){
	for(int k = 1; k <= n; ++k)
		for(int i = 1; i <= n; ++i)
			for(int j = 1; j <= n; ++j)
				dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}

inline void calc(int a, int b){
	memset(data, 0, sizeof(data));
	q.push((lpl){a, 0}); data[a] = 1; int now; lpl lin;
	while(!q.empty()){
		now = q.top().to; q.pop(); vis[now] = false;
		for(int i = point[now].size() - 1; i >= 0; --i){
			lin = point[now][i];
			if(dis[a][lin.to] == dis[a][now] + lin.dis){
				data[lin.to] += data[now];
				if(!vis[lin.to]){q.push((lpl){lin.to, dis[a][lin.to]}); vis[lin.to] = true;}
			}
		}
	}
	md[a][b] = md[b][a] = data[b];
}

inline void workk(){
	floyd();
	for(int i = 1; i <= n; ++i)
		for(int j = i + 1; j <= n; ++j)
			calc(i, j);
//	for(int i = 1; i <= n; ++i)
//		for(int j = i + 1; j <= n; ++j)
//			if(md[i][j] == 0) printf("md[%d][%d] = %d %d
", i, j, md[i][j], dis[i][j]);
}

inline void print(){
	double ans;
	for(int k = 1; k <= n; ++k){
		ans = 0;
		for(int i = 1; i <= n; ++i)
			for(int j = i + 1; j <= n; ++j)
				if(dis[i][k] + dis[k][j] == dis[i][j])
					ans += (double)(md[i][k] * md[k][j]) / md[i][j] * 2;
		printf("%.3lf
", ans);
	}
}

int main()
{
	//freopen("lpl.in", "r", stdin);
	putit();
	workk();
	print();
	return 0;
}