2019/10/21,发现了这题的一个线性递推式,不过不会证明。
F(n)=6∗F(n−1)−8∗F(n−2)−8∗F(n−3)+16∗F(n−4)
题目链接:格子涂油漆
题目描述:
X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形(如下图所示),现需要把这些格子刷上保护漆。
你可以从任意一个格子刷起,刷完一格,可以移动到和它相邻的格子(对角相邻也算数),但不能移动到较远的格子(因为油漆未干不能踩!)
比如:a d b c e f 就是合格的刷漆顺序。
c e f d a b 是另一种合适的方案。
当已知 N 时,求总的方案数。当N较大时,结果会迅速增大,请把结果对 1000000007 (十亿零七) 取模。
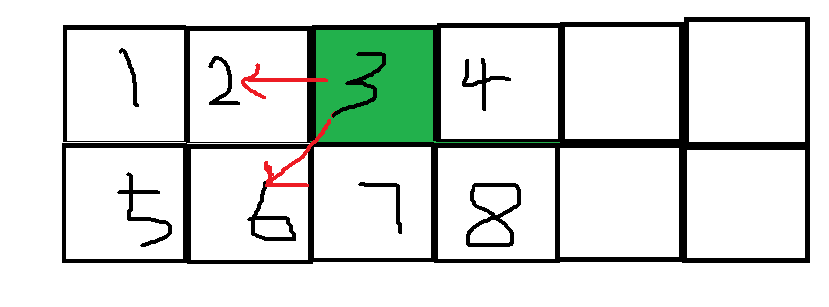
然后就是2或者6走到7,这时就相当于左边已经涂完了,7可以走向4或者8,这时对于右边的终点就没有要求了只要是合理的涂法就行。
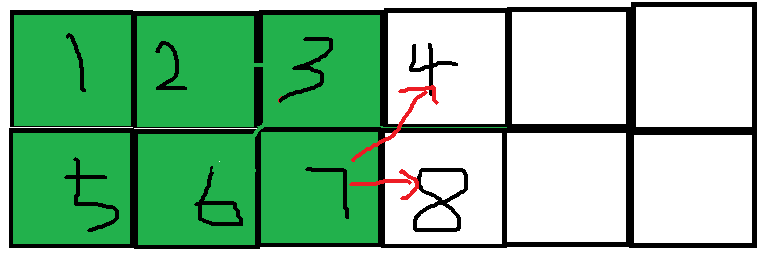
从3走到2或6涂左边的,从7走到4或8涂右边,它们的方案可以总结为两种,一种是以顶点为起点,终点在同一列的方案,另一种就是以顶点为起点,终点任意的方案,所以我们用数组a代表第一种方案,数组b代表第二种方案,那么a[i]就是以一个顶点为起点涂完2*i个格子,终点在起点的同一列的方案,b[i]就是以一个顶点为起点涂完2*i个格子,终点任意的方案。那么从第二列开始到第n-1列中间的列为起点的方案就是
先走左边的方案Li=2*a[i-1]*2*b[n-i]
先走右边的方案Ri=2*b[i-1]*2*a[n-i]
方案就是Ci=(Li+Ri)*2
(就比如上图的第3列为起点,左边就剩下i-1列,右边剩下n-i列,从3开始,先走左边的话,3可以走到2和6,所以左边涂完就是2*a[i-1],然后7可以走到4和8所以右边涂完就是2*b[n-i],左右方案相乘就是这种情况的方案。然后从3开始,也可以先走右边,还有就是也可以从7开始,所以这一列为起点的方案就是(Li+Ri)*2),
那么中间所以列的方案就是C2+C3+...+Cn-1
那么涂完2*n个格子的方案就是4*a[n]+C2+C3+Cn-1(1要特判,因为1列没有4个顶点)
关键在于a数组和b数组怎么得到呢?
a[i]代表的是以一个顶点为起点涂完2*i个格子,终点在起点的同一列的方案,我们以下图为例,假设1是起点,那么5就是终点。一开始1可以走到2和6,如果是走到2,那么2又可以走到3和7,但不能走到6,因为要留下6来走回到5,不然就截断了,对于后面的各列也是同理
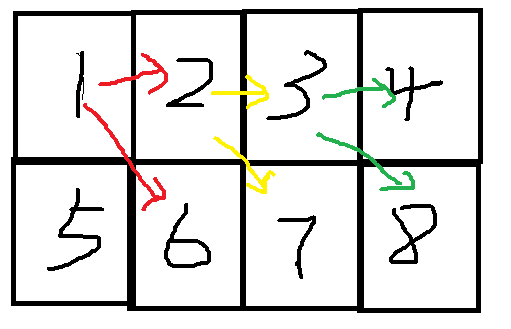
所以就是除了最后一列,每一列有两种方案。也就可以得到a[i]=2i-1
然后b[i]代表的是以一个顶点为起点涂完2*i个格子,终点任意的方案。我们以1为起点的话,它有3种前进的选择2,5,6,那么如果先让1走到5的话,5就可以走到2和6,除去1和5的话,2和6可以视为i-1列的顶点,并且他们为起点终点没有限制
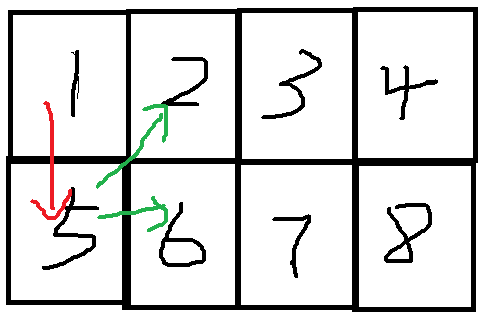
那么这种情况的方案就是2*b[i-1]
然后如果是1先走到下一列也就是2到6的话,
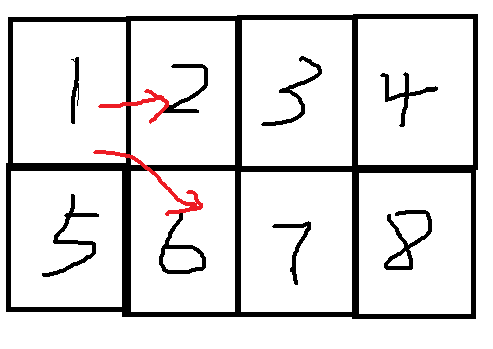
如果终点是5的话,那么这种情况的方案就是a[i]
如果终点不是5的话,那么得先把5给涂掉,就有1,2,5,6,和1,6,5,2两种方案,这时把1,2,5,6去掉,3和7可以视为i-2列的顶点,并且他们为起点终点没有限制
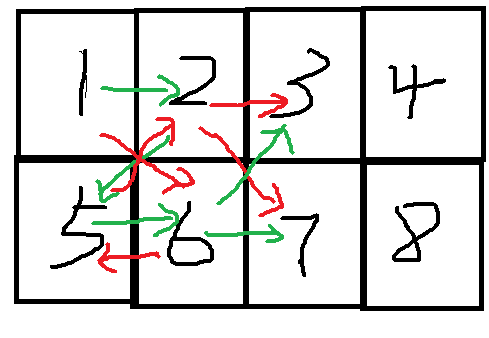
而2和6都可以走到3和7,这种情况的方案就是2*2*b[i-2]
所以就是b[i]=2*a[i-1]+b[i]+4*b[i-2]
加上取模和long long那么这时答案就出来了。

1 #include<cstdio> 2 typedef long long ll; 3 const int N=1108; 4 const ll mod=1000000007; 5 ll b[N]={0},a[N]={0}; 6 int main() 7 { 8 int n; 9 b[1]=1; 10 a[1]=1; 11 b[2]=6; 12 a[2]=2; 13 scanf("%d",&n); 14 if(n==1) 15 { 16 printf("2 "); 17 return 0; 18 } 19 for(int i=3;i<=n;i++) 20 { 21 a[i]=(a[i-1]<<1)%mod; 22 b[i]=(b[i]+(b[i-1]<<1)%mod)%mod; 23 b[i]=(b[i]+a[i])%mod; 24 b[i]=(b[i]+(b[i-2]<<2))%mod; 25 } 26 ll ans=(b[n]<<2)%mod; 27 for(int i=2;i<n;i++) 28 { 29 ll c=((a[i-1]<<1)%mod*(b[n-i]<<1)%mod)%mod; 30 c=(c+((b[i-1]<<1)%mod*(a[n-i]<<1)%mod)%mod)%mod; 31 ans=(ans+(c<<1)%mod)%mod; 32 } 33 printf("%lld ",ans); 34 return 0; 35 }
