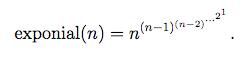整了快一周的指数循环节,虽说自己证明还是不会,但用还是懂用的。
核心东西,降幂公式: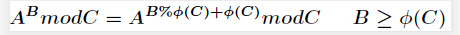
maijing大佬的证明:指数循环节
然后就是直接上题了。
fzu网站好像崩了,这题就直接套版子。
Calculation HDU - 2837
题意: f(0) = 1 and 0^0=1. f(n) = (n%10)^f(n/10) 求f(n)%m。
就递归加指数循环节,f(n)%m = (n%10)^f(n/10)%phi(m)+phi(m)%m,
然后f(n/10)%phi(m)=(n/10%10)^f(n/10/10)%phi(phi(m))+phi(phi(m))%phi(m)
一层层递归,直到n==0的话,此时0^0=1,就返回1%当前要mod的那个数了,而因为不好判断f(x)是不是大于phi(y),所以直接在快速幂里加上判断

1 #include<cstdio> 2 typedef long long ll; 3 ll poww(ll a,ll b,ll c){ 4 if(a>=c) a=a%c+c; 5 ll ans=1; 6 while(b){ 7 if(b&1){ 8 ans=ans*a; 9 if(ans>c) ans=ans%c+c; 10 } 11 a=a*a; 12 if(a>=c) a=a%c+c; 13 b>>=1; 14 } 15 return ans; 16 } 17 int euler(int x){ 18 int ans=x; 19 for(int i=2;i*i<=x;i++){ 20 if(x%i==0){ 21 ans-=ans/i; 22 while(x%i==0) x/=i; 23 } 24 } 25 if(x>1) ans-=ans/x; 26 return ans; 27 } 28 ll f(int x,int y){ 29 if(x==0) return 1%y; 30 return poww(x%10,f(x/10,euler(y)),y); 31 } 32 int main() 33 { 34 int t,n,m; 35 scanf("%d",&t); 36 while(t--){ 37 scanf("%d%d",&n,&m); 38 printf("%lld ",f(n,m)%m); 39 } 40 return 0; 41 }
What is N? HDU - 4335
题意:求满足下列式子的n有多少个
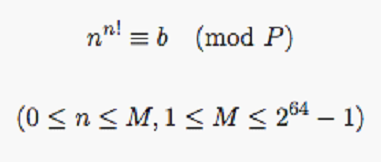
首先,nn!%p=nn!%phi(p)+phi(p)%p,当n<phi(p)的时候,我们就直接套板子暴力算,而当n>=phi(p),n!%phi(p)=0,就是看有多少个nphi(p)%p==b,这时候我们可以把n拆成(phi(p)+k),因为这个时候的指数固定了,(phi(p)+k)phi(p)%p就跟(phi(p)+k)1%p一样,存在着一个长度为p的循环节,我们就找出循环节中包含多少个结果为b的即可。还有个坑点是当p==1的时候,答案很明显是m+1,而m=2的64-1次方的话,答案会超出unsigned long long的范围,得特判。

1 #include<cstdio> 2 typedef unsigned long long ull; 3 const int N=101108; 4 int phi[N],yu[N]; 5 void init(){//预处理欧拉函数 6 for(int i=1;i<N;i++) phi[i]=i; 7 for(int i=2;i<N;i+=2)phi[i]/=2; 8 for(int i=3;i<N;i+=2) if(phi[i]==i){ 9 for(int j=i;j<N;j+=i) phi[j]=phi[j]/i*(i-1); 10 } 11 } 12 ull poww(ull a,ull b,ull c){ 13 ull ans=1; 14 while(b){ 15 if(b&1) ans=ans*a%c; 16 a=a*a%c; 17 b>>=1; 18 } 19 return ans; 20 } 21 int main() 22 { 23 init(); 24 int t=1,T,b,p,pp; 25 ull m; 26 scanf("%d",&T); 27 while(t<=T){ 28 scanf("%d%d%llu",&b,&p,&m); 29 printf("Case #%d: ",t++); 30 if(p==1){ 31 if(m==18446744073709551615ull) printf("18446744073709551616 "); 32 else printf("%llu ",m+1); 33 continue; 34 } 35 pp=phi[p]; 36 ull jc=1,ans=0; 37 for(int i=0;i<pp&&i<=m;i++){//先处理n<phi(p)的情况 38 if(i){ 39 jc*=1ll*i; 40 if(jc>=pp) jc=jc%pp+pp; 41 } 42 if(poww(i,jc,p)==b) ans++; 43 } 44 if(pp<=m){//处理循环节的情况 45 int num=0,lim; 46 for(int i=0;i<p;i++){ 47 yu[i]=poww(pp+i,pp,p); 48 if(yu[i]==b) num++; 49 } 50 ans+=1llu*(m-pp+1)/p*num; 51 lim=(m-pp+1)%p; 52 for(int i=0;i<lim;i++) 53 if(yu[i]==b) ans++; 54 } 55 printf("%llu ",ans); 56 } 57 return 0; 58 }
Strange Limit
题意:a1= p,
an+1= pan for n >= 1,
bn = an mod m!,
求
可以看出就是求a^p^p^p^p^p^p^p^p^p %m!,n个p,n趋向于无穷大,也就是递归里套一个指数循环节,然后居然n趋向于无限大,那么当前要mod的x,phi(phi(phi(m))),也在一直缩小,当p%x=0的时候,就是返回个pp%x,再往上就是0的几次方了,已经没有影响了。
还有就是输出格式有点坑,有个空行。

1 #include<cstdio> 2 typedef long long ll; 3 int p,m,jc[15]={1}; 4 int euler(int x){ 5 int ans=x; 6 for(int i=2;i*i<=x;i++){ 7 if(x%i==0){ 8 ans-=ans/i; 9 while(x%i==0) x/=i; 10 } 11 } 12 if(x>1) ans-=ans/x; 13 return ans; 14 } 15 ll poww(ll a,ll b,ll c){ 16 ll ans=1; 17 if(a>=c) a=a%c+c; 18 while(b){ 19 if(b&1){ 20 ans*=a; 21 if(ans>=c) ans=ans%c+c; 22 } 23 a*=a; 24 if(a>=c) a=a%c+c; 25 b>>=1; 26 } 27 return ans; 28 } 29 ll ap(int x){ 30 if(p%x==0) return poww(p,p,x); 31 return poww(p,ap(euler(x)),x); 32 } 33 int main() 34 { 35 for(int i=1;i<=12;i++) jc[i]=jc[i-1]*i; 36 int flag=0; 37 while(~scanf("%d%d",&p,&m)){ 38 if(flag) printf(" "); 39 flag=1; 40 printf("%lld ",ap(jc[m])%jc[m]); 41 } 42 return 0; 43 }
计蒜客Exponial
也是一个递归加指数循环节,需要注意的地方就是,递归出口有两个,一个是n==1的时候,因为一个就和上面那题思路一样,当x%y==0,返回个xx-1%y

1 #include<cstdio> 2 typedef long long ll; 3 int euler(int x){ 4 int ans=x; 5 for(int i=2;i*i<=x;i++){ 6 if(x%i==0){ 7 ans-=ans/i; 8 while(x%i==0) x/=i; 9 } 10 } 11 if(x>1) ans-=ans/x; 12 return ans; 13 } 14 ll poww(ll a,ll b,ll c){ 15 ll ans=1; 16 if(a>=c) a=a%c+c; 17 while(b){ 18 if(b&1){ 19 ans*=a; 20 if(ans>=c) ans=ans%c+c; 21 } 22 a*=a; 23 if(a>=c) a=a%c+c; 24 b>>=1; 25 } 26 return ans; 27 } 28 ll exponial(int x,int y){ 29 if(x==1) return 1%y; 30 if(x%y==0) return poww(x,x-1,y); 31 return poww(x,exponial(x-1,euler(y)),y); 32 } 33 int main() 34 { 35 int n,m; 36 while(~scanf("%d%d",&n,&m)){ 37 printf("%lld ",exponial(n,m)%m); 38 } 39 return 0; 40 }
Brute-force Algorithm HDU - 3221
题意:
给出n,求funny运行了多少次。
可以看出F[1]=a,F[2]=b,而F[3]=F[1]*F[2]=a*b,F[4]=F[3]*F[2]=a*b*b。。。F[n]=F[n-1]*F[n-2]
那么当n>=3时,a的指数也就是斐波那契第n-3项,b是n-2项(我是以f[0]=1,f[1]=1来算)
这是就是矩阵快速幂去求出他们的指数,然后指数进行欧拉降幂

1 #include<cstdio> 2 typedef long long ll; 3 ll a,b,n,md,mmd; 4 struct Matrix{ 5 int r,c; 6 ll a[5][5]; 7 Matrix(){} 8 Matrix(int r,int c):r(r),c(c){ 9 for(int i=0;i<r;i++) 10 for(int j=0;j<c;j++) a[i][j]=0; 11 } 12 }; 13 Matrix mmul(Matrix m1,Matrix m2,ll z){ 14 Matrix ans(m1.r,m2.c); 15 for(int i=0;i<m1.r;i++) 16 for(int j=0;j<m2.c;j++) 17 for(int k=0;k<m1.c;k++){ 18 ans.a[i][j]+=m1.a[i][k]*m2.a[k][j]; 19 if(ans.a[i][j]>=z) ans.a[i][j]=ans.a[i][j]%z+z; 20 } 21 return ans; 22 } 23 Matrix mpow(Matrix m1,ll y,ll z){ 24 Matrix ans(m1.r,m1.c); 25 for(int i=0;i<ans.r;i++) ans.a[i][i]=1; 26 while(y){ 27 if(y&1) ans=mmul(ans,m1,z); 28 m1=mmul(m1,m1,z); 29 y>>=1; 30 } 31 return ans; 32 } 33 ll euler(ll x){ 34 ll ans=x; 35 for(int i=2;i*i<=x;i++){ 36 if(x%i==0){ 37 ans-=ans/i; 38 while(x%i==0) x/=i; 39 } 40 } 41 if(x>1) ans-=ans/x; 42 return ans; 43 } 44 ll poww(ll x,ll y,ll z){ 45 ll ans=1; 46 while(y){ 47 if(y&1) ans=ans*x%z; 48 x=x*x%z; 49 y>>=1; 50 } 51 return ans; 52 } 53 int main(){ 54 int t=1,C; 55 scanf("%d",&C); 56 while(t<=C){ 57 scanf("%lld%lld%lld%lld",&a,&b,&md,&n); 58 printf("Case #%d: ",t++); 59 if(n==1) printf("%lld ",a%md); 60 else if(n==2) printf("%lld ",b%md); 61 else{ 62 n-=3; 63 mmd=euler(md); 64 Matrix A(2,1),T(2,2); 65 A.a[0][0]=A.a[1][0]=1; 66 T.a[0][0]=T.a[0][1]=T.a[1][0]=1; 67 T=mpow(T,n,mmd); 68 A=mmul(T,A,mmd); 69 // printf("%lld**",mmd); 70 // printf("%lld %lld ",A.a[0][0],A.a[1][0]); 71 ll ans=poww(a,A.a[1][0],md); 72 ans=ans*poww(b,A.a[0][0],md); 73 printf("%lld ",ans%md); 74 } 75 } 76 return 0; 77 }
啊,感觉数学这些东西就是,先记住怎么用了,证明看了也不一定会,记了也会忘
主要是想学广义斐波那契数列的指数循环节的,但多校没补的题有点多,再见。