首先我们来百度一下,欧拉路径以及回路的定义:
若图G中存在这样一条路径,使得它恰通过G中每条边一次,则称该路径为欧拉路径。若该路径是一个圈,则称为欧拉(Euler)回路。
具有欧拉回路的图称为欧拉图(简称E图)。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。
通俗来说,就是欧拉路径就是图中的每条边经过却只经过一次的路径,而最后回到起点的路径就是欧拉回路。
那给你一个图怎么判断存不存在,欧拉路径或者欧拉回路呢
首先,判断图是不是连通的,这个就很简单了,dfs或者并查集都可以。
然后就是根据定理
欧拉路径的定理
连通的无向图有欧拉路径的充要条件是:
G中奇顶点(连接的边数量为奇数的顶点)的数目等于0或者2。
连通的无向图是欧拉环(存在欧拉回路)的充要条件是:
G中每个顶点的度都是偶数。
欧拉回路的定理
无向图存在欧拉回路的充要条件
一个无向图存在欧拉回路,当且仅当该图所有顶点度数都为偶数,且该图是连通图。
有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路,所有顶点的入度等于出度且该图是连通图。
这四个定理很好理解,无向图的话,因为要把所有边走一遍且只走一边,那对于每个点来说,如果不是起点或者终点的话,那么度数应该是偶数,有一条进边就有一条对于的出边,然后是起点,出边应该多一条,终点应该入边多一条,所以度数是奇数。然后如果没有奇数点的话,那就是任意点都可以作为起点并且能走回它,那就是存在一个回路了,否则就是得两个奇数点,一个起点和一个终点。
有向图的话,就是分为入度出度,道理是一样的,然后我们就可以来做题了
欧拉回路
中文题,真模板题,给一个无向图,问存不在在欧拉回路,存在扣1,不存在扣0.
直接并查集判断连通性,只能有一个连通集,然后判断度数,不存在奇数度的点,就ok了。

1 #include<cstdio> 2 const int N=1108; 3 int fa[N],in[N]; 4 int find(int x){ 5 return fa[x]==x ? x : fa[x]=find(fa[x]); 6 } 7 void bing(int x,int y){ 8 int fx=find(x),fy=find(y); 9 if(fx!=fy) fa[fx]=fy; 10 return ; 11 } 12 int main(){ 13 int n,m,u,v; 14 while(scanf("%d%d",&n,&m)&&n){ 15 for(int i=0;i<=n;i++){ 16 fa[i]=i; 17 in[i]=0; 18 } 19 while(m--){ 20 scanf("%d%d",&u,&v); 21 in[u]++; 22 in[v]++; 23 bing(u,v); 24 } 25 int flag=1,num=0; 26 for(int i=1;i<=n;i++){ 27 fa[i]=find(fa[i]); 28 if(fa[i]==i) num++; 29 if(num>1) flag=0; 30 if(in[i]&1) flag=0; 31 if(!flag) break; 32 } 33 printf("%d ",flag); 34 } 35 return 0; 36 }
Ant Trip HDU - 3018
题意:给一个无向图问,最少分几组能够把所有边走且走一遍?
要把所有边走且只走一遍,其实就是在求一个欧拉路径,但一条路径不一定能把所有边走完,这里要求的就是最少分出多少条欧拉路径。
我们从无向图的欧拉路径定理下手,图中奇顶点(连接的边数量为奇数的顶点)的数目等于0或者2。
那我们先用并查集判断有多少个连通集,然后对于每个连通集,如果它没有奇度点的话,那么一条欧拉路径就能把它的边走完,那如果它的奇度点的个数为x的话,每2个奇度点就能走一条欧拉路径,所以最少就需要(x+1)/2条。

1 #include<cstdio> 2 const int N=100118; 3 int fa[N],in[N],num[N]; 4 int find(int x){ 5 return fa[x]==x ? x : fa[x]=find(fa[x]); 6 } 7 void bing(int x,int y){ 8 int fx=find(x),fy=find(y); 9 if(fx!=fy) fa[fx]=fy; 10 return ; 11 } 12 int main(){ 13 int n,m,u,v; 14 while(~scanf("%d%d",&n,&m)){ 15 for(int i=0;i<=n;i++){ 16 fa[i]=i; 17 in[i]=0; 18 num[i]=0; 19 } 20 while(m--){ 21 scanf("%d%d",&u,&v); 22 in[u]++; 23 in[v]++; 24 bing(u,v); 25 } 26 for(int i=1;i<=n;i++){ 27 fa[i]=find(fa[i]); 28 if(in[i]&1) num[fa[i]]++; 29 } 30 int ans=0; 31 for(int i=1;i<=n;i++){ 32 if(fa[i]!=i) continue; 33 if(!num[i]&&in[i]) ans++; 34 else if(num[i]) ans+=(num[i]+1)/2; 35 } 36 printf("%d ",ans); 37 } 38 return 0; 39 }
Play on Words UVA - 10129
题意:给两个单词,如果其中一个的最后一个单词等于另外一个的第一个单词的话,那就可以把它们串起来,问能不能把所有单词串起来。
单纯看每个单词的话,那就是得在每两个能串的单词之间连一条边,1e5个单词,这样很明显直接会T,我们想一下,如果一个单词能和其他单词串起来,那不就是它首字母的入度+1或者尾字母的出度+1,然后每个单词其实就是它首字母和尾字母的一条有向边。
这样把所有单词串起来,就是问有向图有没有欧拉路径,我们根据定理判断就ok了。

1 #include<cstdio> 2 #include<cstring> 3 int in[28],out[28],fa[28]; 4 int find(int x){ 5 return fa[x]==x ? x : fa[x]=find(fa[x]); 6 } 7 void bing(int x,int y){ 8 int fx=find(x),fy=find(y); 9 if(fx!=fy) fa[fx]=fy; 10 return ; 11 } 12 char s[1010]; 13 int main(){ 14 int t,n,lens; 15 scanf("%d",&t); 16 while(t--){ 17 scanf("%d",&n); 18 for(int i=0;i<=26;i++){ 19 fa[i]=i; 20 in[i]=out[i]=0; 21 } 22 for(int i=0;i<n;i++){ 23 scanf("%s",s); 24 lens=strlen(s); 25 in[s[0]-'a']++; 26 out[s[lens-1]-'a']++; 27 bing(s[0]-'a',s[lens-1]-'a'); 28 } 29 int flag=1,num1=0,num2=0,num3=0; 30 for(int i=0;i<26;i++){ 31 if(in[i]-out[i]==1) num1++; 32 else if(out[i]-in[i]==1) num2++; 33 else if(in[i]!=out[i]) flag=0; 34 if(find(fa[i])==i&&(in[i]||out[i])) num3++; 35 if(num1>1||num2>1||num3>1) flag=0; 36 if(!flag) break; 37 } 38 // printf("%d %d %d %d ",flag,num1,num2,num3); 39 if(flag&&num1==num2) printf("Ordering is possible. "); 40 else printf("The door cannot be opened. "); 41 } 42 return 0; 43 }
知道怎么判定有没有欧拉路径或者欧拉回路了,那怎么求欧拉路径或者欧拉回路呢?
两个方法,套圈(暴搜)法或者fleury算法。
首先是套圈法,先上代码。

1 void dfs(int u){ 2 for(int i=1;i<=n;i++){ 3 if(ok[u][i]){ 4 ok[u][i]--; 5 ok[i][u]--; 6 dfs(i); 7 } 8 } 9 ans[cnt++]=u; 10 }
什么意思呢,从一个点出发,能走到哪个点我们就走到哪个点,并且把这条边删除掉,直到这个点走不到其他点了,我们就把它记录下来,然后再把记录点逆序输出。
为什么呢?首先我们先判断有没有欧拉路径或者欧拉回路,有的话那肯定是能走出来的。
然后起点,对于欧拉回路的话,任意点可以作为起点,而欧拉路径的话我们以一个奇度点为起点。从起点出发走,当一个点已经无边可走了,那说明它是当前一个终点或是一个圈的起点。
我们来模拟一下。
第一个图这个1到2到3没路了,这时候很明显3是终点了,开始回溯。
第二图的话,3到2到1到3到4到6到5到4,这样的话4是终点,开始回溯是能走出一条欧拉路径,但我们不可能限定3一定先走到2,可能的是3先走到4。
这时候就是,3走到4,4到6,6到5,5到4,没有路了,把4记录下来,然后回到5,也没路了,再记录下来,接下来6,4,也是一样,直到3,3还能到1,那我们继续走3,1,2,到3没路了,回溯。
欧拉路径我们把逆序把记录的点输出就是3,2,1,3,4,6,5,4,也就是3,2,1,3这个圈再套上了4,6,5,4这个圈。

套圈法的意思其实就是,因为欧拉路径要么一个点同时做起点和终点(回路),或者一个做起点,一个做终点,那么当走到一个点不能再走时,很明显它就是当前的一个终点了,我们就开始回溯,但有可能的就是我们中途走了‘’桥”,如上面的3-4,所以回溯时有点还能继续往下走我们就让它先走,然后再走“桥”。
这样其实就是如果只有一个圈,那就是直接走到终点回溯,多个圈的话,就是先走了圈,然后再走“桥”,把它跟其他桥套起来。
实现上其实就是像上面代码写的,一个点能走到那个点就走,同时把走的这条边删除(注意无向边和有向边),直到一个点无边可走,记录下来,回溯,也就是个dfs过程。
然后fleury算法的话,直接引用guomutian911的博客Fleury (弗罗莱) 算法通俗解释

网上也很多这个算法的代码以及解释,我就不多重复了,从代码量和运行时间来说,我觉得套圈法是更优的,然后直接来上题。
中文题,意思就是给定了连通并且保证能有解的无向图,要按字典序最小输出无向图的欧拉路径。
就先判断有没有奇度点,有的话以最小那个为起点,否则以1为起点,然后就是直接dfs了。cur的话是类似最大流里面的一个当前弧优化,不懂没关系。

1 #include<cstdio> 2 const int N=520; 3 int n,cnt,in[N],cur[N],ok[N][N],ans[N*10]; 4 void dfs(int u){ 5 for(int &i=cur[u];i<=500;i++){ 6 if(ok[u][i]){ 7 ok[u][i]--; 8 ok[i][u]--; 9 dfs(i); 10 } 11 } 12 ans[cnt++]=u; 13 } 14 int main(){ 15 int u,v; 16 while(~scanf("%d",&n)){ 17 for(int i=1;i<=500;i++){ 18 in[i]=0; 19 cur[i]=1; 20 for(int j=1;j<=500;j++) 21 ok[i][j]=0; 22 } 23 for(int i=0;i<n;i++){ 24 scanf("%d%d",&u,&v); 25 in[u]++; 26 in[v]++; 27 ok[u][v]++; 28 ok[v][u]++; 29 } 30 int beg=1; 31 for(int i=1;i<=500;i++) if(in[i]&1){ 32 beg=i; 33 break; 34 } 35 cnt=0; 36 dfs(beg); 37 for(int i=cnt-1;i>=0;i--) printf("%d ",ans[i]); 38 } 39 return 0; 40 }

1 #include<cstdio> 2 const int N=520; 3 int n,cnt,sn,in[N],ok[N][N],sta[N*10],ans[N*10],cur[N]; 4 void dfs(int u){ 5 sta[++sn]=u; 6 for(int &i=cur[u];i<=500;i++){ 7 if(ok[u][i]){ 8 ok[u][i]--; 9 ok[i][u]--; 10 dfs(i); 11 break; 12 } 13 } 14 } 15 void fleury(int beg){ 16 sn=cnt=0; 17 sta[++sn]=beg; 18 int u,flag; 19 while(sn){ 20 flag=0; 21 u=sta[sn]; 22 for(int &i=cur[u];i<=500;i++){ 23 if(ok[u][i]){ 24 flag=1; 25 break; 26 } 27 } 28 if(!flag) ans[cnt++]=sta[sn--]; 29 else dfs(sta[sn--]); 30 } 31 return ; 32 } 33 int main(){ 34 int u,v; 35 while(~scanf("%d",&n)){ 36 for(int i=1;i<=500;i++){ 37 in[i]=0; 38 for(int j=1;j<=500;j++) 39 ok[i][j]=0; 40 } 41 for(int i=0;i<n;i++){ 42 scanf("%d%d",&u,&v); 43 in[u]++; 44 in[v]++; 45 ok[u][v]++; 46 ok[v][u]++; 47 } 48 int beg=1; 49 for(int i=1;i<=500;i++) if(in[i]&1){ 50 beg=i; 51 break; 52 } 53 fleury(beg); 54 for(int i=cnt-1;i>=0;i--) printf("%d ",ans[i]); 55 } 56 return 0; 57 }
HZNUOJ Little Sub and Traveling
题意: 一个数x,下一步可以走到,x*2%n或者(x*2+1)%n,给你一个n,要你找一条从0开始,然后0~n-1的数走且只走过一次最终回到0的字典序最大的路径。
看似是每个点只走过一次,是找一个哈密顿回路,其实要找的还是一个欧拉回路。
首先n是奇数,没有答案输出-1,这个暴力打表也可以看出来,那为什么呢,因为可以到0的点只有n/2这个数,这个数还有n是奇数的话,n-1这个数也是只能由n/2这个数走到,那n/2不可能走到其中一个之后又回到它走到另外一个,所以无解。
然后n是偶数的话,我们看x(<=n/2)可以走到,x*2%n以及(x*2+1)%n,而x+n/2可以走到 (x*2+n)%n (x*2+n+1)%n,也就是x跟x+n/2的下一步是一样的话,如果我们把它们两个看成一个整体的话,也就是剩下n/2个点,然后每个点两个入度,两个出度,也就是求一个欧拉回路了。
比如n等于8的时候就像下图这样,所以直接套圈走起。
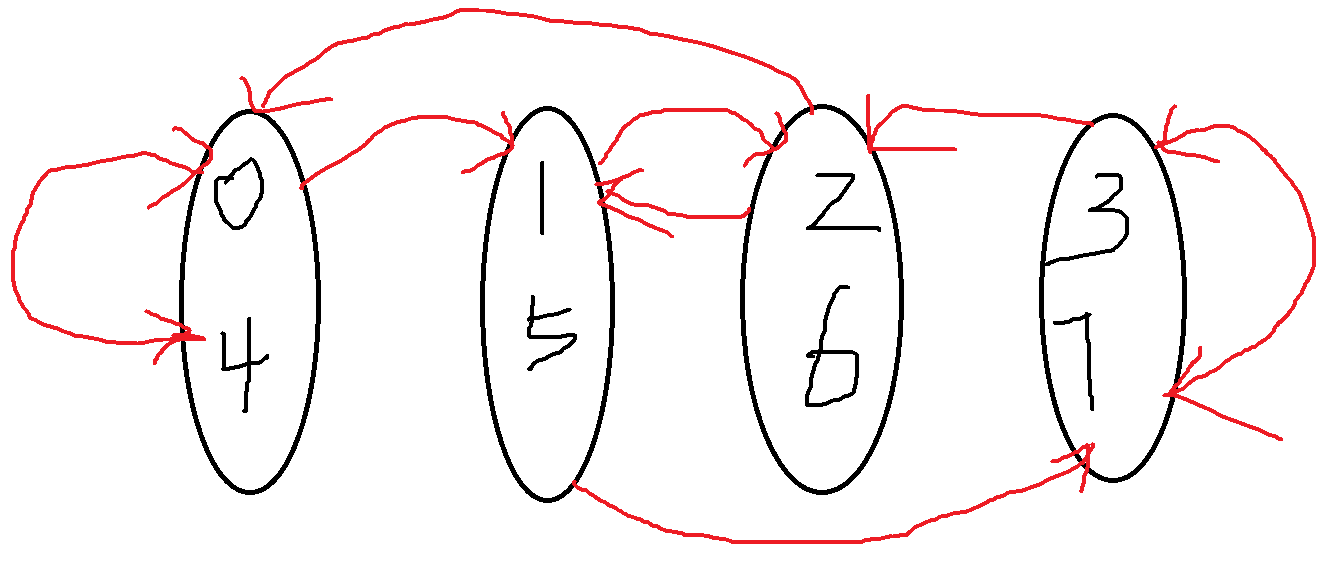

1 #include<cstdio> 2 int n,cnt,vis[10118],ans[10118]; 3 void dfs(int x){ 4 int x1=(x*2+1)%n,x2=x*2%n; 5 if(!vis[x1]){ 6 vis[x1]=1; 7 dfs(x1); 8 } 9 if(!vis[x2]){ 10 vis[x2]=1; 11 dfs(x2); 12 } 13 ans[cnt++]=x; 14 return ; 15 } 16 int main(){ 17 while(~scanf("%d",&n)){ 18 if(n&1) printf("-1 "); 19 else{ 20 for(int i=0;i<n;i++) vis[i]=0; 21 cnt=0; 22 dfs(0); 23 for(int i=cnt-1;i>=0;i--) printf("%d%c",ans[i]," "[i==0]); 24 } 25 } 26 return 0; 27 }
中文题,无敌大整合,给你无向或者有向边,问有没有欧拉回路,没有就NO,有的话就YES然后输出任意答案。
判断连通,然后用定理判断,最后套圈法,就这样一气呵成,注意的是这里要输出的是边的编号,所以记录的是边不是点,还有就是这题不用当前弧优化会超时,不知道是什么的,可以去了解一下。

1 #include<cstdio> 2 const int N=101108,M=201108; 3 struct Side{ 4 int v,ne,ok,id; 5 }S[M<<1]; 6 int t,n,m,sn,cnt,head[N],cur[N],in[N],out[N],fa[N],ans[M<<1]; 7 void init(){ 8 sn=0; 9 for(int i=1;i<=n;i++){ 10 fa[i]=i; 11 head[i]=-1; 12 in[i]=out[i]=0; 13 } 14 } 15 void add(int u,int v,int id){ 16 S[sn].ok=1; 17 S[sn].id=id; 18 S[sn].v=v; 19 S[sn].ne=head[u]; 20 head[u]=sn++; 21 } 22 int find(int x){ 23 return fa[x]==x ? x : fa[x]=find(fa[x]); 24 } 25 void bing(int x,int y){ 26 int fx=find(x),fy=find(y); 27 if(fx!=fy) fa[fx]=fy; 28 return ; 29 } 30 void dfs(int u){ 31 for(int &i=cur[u];~i;i=S[i].ne){ 32 if(S[i].ok){ 33 S[i].ok=0; 34 int temp=i; 35 if(t==1) S[i^1].ok=0; 36 dfs(S[i].v); 37 ans[cnt++]=S[temp].id; 38 if(i==-1) break; 39 } 40 } 41 } 42 int main(){ 43 int u,v; 44 while(~scanf("%d",&t)){ 45 scanf("%d%d",&n,&m); 46 init(); 47 for(int i=1;i<=m;i++){ 48 scanf("%d%d",&u,&v); 49 bing(u,v); 50 if(t==1){ 51 in[u]++; 52 in[v]++; 53 add(u,v,i); 54 add(v,u,-i); 55 }else{ 56 in[v]++; 57 out[u]++; 58 add(u,v,i); 59 } 60 } 61 int beg=1,flag=1,num=0; 62 for(int i=1;i<=n;i++){ 63 cur[i]=head[i]; 64 if(fa[i]==i&&in[i]) num++; 65 if(t==1){ 66 if(in[i]&1) flag=0; 67 else if(in[i]) beg=i; 68 }else{ 69 if(in[i]!=out[i]) flag=0; 70 else if(in[i]) beg=i; 71 } 72 if(!flag||num>1) break; 73 } 74 if(flag&&num<=1){ 75 printf("YES "); 76 if(num){ 77 cnt=0; 78 dfs(beg); 79 for(int i=cnt-1;i>=0;i--) printf("%d%c",ans[i]," "[i==0]); 80 } 81 }else printf("NO "); 82 } 83 return 0; 84 }
那如果是一个混合图的话,我们怎么办呢?
这涉及到最大流,不会最大流的可以去学一下。
具体步骤的话,直接引用Adela的混合图中欧拉回路,我就不重复了,直接说为什么。
想法其实就是,因为有向边的方向已经固定了,这没法更改,我们这样就是看能不能给无向边定一个方向,然后把整个图成为有向图,然后就是有向图的判定了。
而这个给定方向就是就是通过最大流的调整了,有向边就是统计入度出度,对于每条a与b之间无向边,我们先假定一个a->b的方向,然后统计出度入度,以及建一条流量为1从a到b的边,说明a到b之间有一条可以反向的无向边。
如果存在出度与入度奇偶性不同的点的话,肯定就不存在欧拉回路了,因为改变一条无向边的方向,对于两边的点来说,也就是出度-1,入度+1,或者出度+1,入度-1,奇偶性变化是一样的,如果一开始奇偶性就不同的话,肯定没法使得出度等于入度。
然后对于每个出度大于入度的点,我们把它与源点连一条流量为(出度-入度)/2的边,(出度-入度)/2其实就是需要改变多少条连到它上面的无向边,使得它出度等于入度。而对于入度大于出度的点,则是与汇点连一条流量为(入度-出度)/2的边。
所以最终能不能有欧拉回路,也就是看能不能满流,让每个点都满足出度等于入度的要求。
而欧拉路径的话,就是最多只能有两个出度与入度奇偶性不同的点,也就是终点和起点,然后我们找到这两个点,给它们连一条无向边,那处理就跟欧拉回路的一样了。
至于路径的输出,我们就看之前流量为1的那些边,如果流量变为0了,说明反向了,否则就是我们原定的方向,就用这些新的有向边和原来的有向边,然后有向图的欧拉回路就ok了。
直接挂三道题,题意就不说了,练一下英语吧~~~~~~~~

1 #include<cstdio> 2 #include<cstring> 3 #include<queue> 4 #include<algorithm> 5 using namespace std; 6 const int N=36,M=2118,inf=1e9+7; 7 struct Node{ 8 int v,ne,w; 9 }S[M<<1]; 10 char s[N]; 11 int sn,sb,se,head[N],cur[N],dep[N]; 12 int n,in[N],out[N],fa[N]; 13 void init(){ 14 sn=0; 15 sb=26,se=27; 16 for(int i=0;i<=se;i++){ 17 fa[i]=i; 18 head[i]=-1; 19 in[i]=out[i]=0; 20 } 21 } 22 int find(int x){ 23 return fa[x]==x ? x : fa[x]=find(fa[x]); 24 } 25 void bing(int x,int y){ 26 int fx=find(x),fy=find(y); 27 if(fx!=fy) fa[fx]=fy; 28 return ; 29 } 30 void add(int u,int v,int w){ 31 S[sn].w=w; 32 S[sn].v=v; 33 S[sn].ne=head[u]; 34 head[u]=sn++; 35 } 36 void addE(int u,int v,int w){ 37 add(u,v,w); 38 add(v,u,0); 39 } 40 bool bfs(){ 41 for(int i=0;i<=se;i++) dep[i]=0; 42 dep[sb]=1; 43 queue<int> q; 44 q.push(sb); 45 int u,v; 46 while(!q.empty()){ 47 u=q.front(); 48 q.pop(); 49 for(int i=head[u];~i;i=S[i].ne){ 50 v=S[i].v; 51 if(S[i].w>0&&!dep[v]){ 52 dep[v]=dep[u]+1; 53 if(v==se) return true; 54 q.push(v); 55 } 56 } 57 } 58 return false; 59 } 60 int dfs(int u,int minf){ 61 if(u==se||!minf) return minf; 62 int v,flow; 63 for(int &i=cur[u];~i;i=S[i].ne){ 64 v=S[i].v; 65 if(S[i].w>0&&dep[v]==dep[u]+1){ 66 flow=dfs(v,min(minf,S[i].w)); 67 if(flow){ 68 S[i].w-=flow; 69 S[i^1].w+=flow; 70 return flow; 71 } 72 } 73 } 74 return 0; 75 } 76 int dinic(){ 77 int maxf=0,flow; 78 while(bfs()){ 79 for(int i=0;i<=se;i++) cur[i]=head[i]; 80 while(flow=dfs(sb,inf)) maxf+=flow; 81 } 82 return maxf; 83 } 84 int main(){ 85 int t=1,T,u,v,op,lens; 86 scanf("%d",&T); 87 while(t<=T){ 88 init(); 89 scanf("%d",&n); 90 for(int i=0;i<n;i++){ 91 scanf("%s%d",s,&op); 92 lens=strlen(s); 93 u=s[0]-'a'; 94 v=s[lens-1]-'a'; 95 in[v]++; 96 out[u]++; 97 bing(u,v); 98 if(op) addE(u,v,1); 99 } 100 int num1=0,num2=0,x1=-1,x2=-1; 101 for(int i=0;i<26;i++){ 102 if(fa[i]==i&&(in[i]||out[i])) num1++; 103 if((in[i]-out[i])&1){ 104 num2++; 105 if(x1==-1) x1=i; 106 else x2=i; 107 } 108 if(num1>1||num2>2) break; 109 } 110 printf("Case %d: ",t++); 111 if(num1!=1||num2>2||num2==1){ 112 printf("Poor boy! "); 113 continue; 114 } 115 if(num2==2){ 116 in[x1]++; 117 out[x2]++; 118 addE(x2,x1,1); 119 } 120 int sum1=0,sum2=0; 121 for(int i=0;i<26;i++){ 122 if(in[i]==out[i]) continue; 123 if(in[i]>out[i]){ 124 sum1+=(in[i]-out[i])/2; 125 addE(i,se,(in[i]-out[i])/2); 126 } 127 else{ 128 sum2+=(out[i]-in[i])/2; 129 addE(sb,i,(out[i]-in[i])/2); 130 } 131 } 132 // printf("%d %d %d ",sum1,sum2,dinic()); 133 if(sum1!=sum2||dinic()!=sum1) printf("Poor boy! "); 134 else printf("Well done! "); 135 } 136 return 0; 137 }

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N=218,M=2108,inf=1e9+7; 5 struct Node{ 6 int v,ne,w; 7 }S[M<<1]; 8 int sn,sb,se,head[N],cur[N],dep[N]; 9 int n,m,in[N],out[N],q[201108]; 10 void init(){ 11 sn=0; 12 sb=0,se=n+1; 13 for(int i=sb;i<=se;i++){ 14 head[i]=-1; 15 in[i]=out[i]=0; 16 } 17 } 18 void add(int u,int v,int w){ 19 S[sn].w=w; 20 S[sn].v=v; 21 S[sn].ne=head[u]; 22 head[u]=sn++; 23 } 24 void addE(int u,int v,int w){ 25 add(u,v,w); 26 add(v,u,0); 27 } 28 bool bfs(){ 29 for(int i=sb;i<=se;i++) dep[i]=0; 30 dep[sb]=1; 31 int u,v,qn=0; 32 q[++qn]=sb; 33 while(qn>0){ 34 u=q[qn]; 35 qn--; 36 for(int i=head[u];~i;i=S[i].ne){ 37 v=S[i].v; 38 if(S[i].w>0&&!dep[v]){ 39 dep[v]=dep[u]+1; 40 if(v==se) return true; 41 q[++qn]=v; 42 } 43 } 44 } 45 return false; 46 } 47 int dfs(int u,int minf){ 48 if(u==se||!minf) return minf; 49 int v,flow; 50 for(int &i=cur[u];~i;i=S[i].ne){ 51 v=S[i].v; 52 if(S[i].w>0&&dep[v]==dep[u]+1){ 53 flow=dfs(v,min(minf,S[i].w)); 54 if(flow){ 55 S[i].w-=flow; 56 S[i^1].w+=flow; 57 return flow; 58 } 59 } 60 } 61 return 0; 62 } 63 int dinic(){ 64 int maxf=0,flow; 65 while(bfs()){ 66 for(int i=sb;i<=se;i++) cur[i]=head[i]; 67 while(flow=dfs(sb,inf)) maxf+=flow; 68 } 69 return maxf; 70 } 71 int main(){ 72 int t,u,v,d; 73 scanf("%d",&t); 74 while(t--){ 75 scanf("%d%d",&n,&m); 76 init(); 77 for(int i=0;i<m;i++){ 78 scanf("%d%d%d",&u,&v,&d); 79 in[v]++,out[u]++; 80 if(!d) addE(u,v,1); 81 } 82 int flag=1,sum1=0,sum2=0; 83 for(int i=1;i<=n;i++){ 84 if(in[i]==out[i]) continue; 85 if((in[i]-out[i])&1){ 86 flag=0; 87 break; 88 } 89 else if(out[i]>in[i]){ 90 sum1+=(out[i]-in[i])/2; 91 addE(sb,i,(out[i]-in[i])/2); 92 } 93 else{ 94 sum2+=(in[i]-out[i])/2; 95 addE(i,se,(in[i]-out[i])/2); 96 } 97 } 98 if(!flag||sum1!=sum2||dinic()!=sum1) printf("impossible "); 99 else printf("possible "); 100 } 101 return 0; 102 }

1 #include<cstdio> 2 #include<queue> 3 #include<algorithm> 4 using namespace std; 5 const int N=118,M=1108,inf=1e9+7; 6 struct Node{ 7 int v,ne,w; 8 }S[M<<1],U[M<<1]; 9 char s[5]; 10 int sn,sb,se,head[N],cur[N],dep[N]; 11 int n,m,in[N],out[N],ok[N][N]; 12 int un,headu[N],cnt,ans[M<<1]; 13 void init(){ 14 sn=un=0; 15 sb=0,se=n+1; 16 for(int i=sb;i<=se;i++){ 17 head[i]=headu[i]=-1; 18 in[i]=out[i]=0; 19 for(int j=sb;j<=se;j++) ok[i][j]=0; 20 } 21 } 22 void add(int u,int v,int w){ 23 S[sn].w=w; 24 S[sn].v=v; 25 S[sn].ne=head[u]; 26 head[u]=sn++; 27 } 28 void addE(int u,int v,int w){ 29 add(u,v,w); 30 add(v,u,0); 31 } 32 void addu(int u,int v,int w){ 33 U[un].w=w; 34 U[un].v=v; 35 U[un].ne=headu[u]; 36 headu[u]=un++; 37 } 38 bool bfs(){ 39 for(int i=sb;i<=se;i++) dep[i]=0; 40 dep[sb]=1; 41 queue<int> q; 42 q.push(sb); 43 int u,v; 44 while(!q.empty()){ 45 u=q.front(); 46 q.pop(); 47 for(int i=head[u];~i;i=S[i].ne){ 48 v=S[i].v; 49 if(S[i].w>0&&!dep[v]){ 50 dep[v]=dep[u]+1; 51 if(v==se) return true; 52 q.push(v); 53 } 54 } 55 } 56 return false; 57 } 58 int dfs(int u,int minf){ 59 if(u==se||!minf) return minf; 60 int v,flow; 61 for(int &i=cur[u];~i;i=S[i].ne){ 62 v=S[i].v; 63 if(S[i].w>0&&dep[v]==dep[u]+1){ 64 flow=dfs(v,min(minf,S[i].w)); 65 if(flow){ 66 S[i].w-=flow; 67 S[i^1].w+=flow; 68 return flow; 69 } 70 } 71 } 72 return 0; 73 } 74 int dinic(){ 75 int maxf=0,flow; 76 while(bfs()){ 77 for(int i=sb;i<=se;i++) cur[i]=head[i]; 78 while(flow=dfs(sb,inf)) maxf+=flow; 79 } 80 return maxf; 81 } 82 void dfs2(int u){ 83 for(int &i=cur[u];i<=n;i++) 84 if(ok[u][i]){ 85 ok[u][i]--; 86 dfs2(i); 87 } 88 ans[cnt++]=u; 89 } 90 int main(){ 91 int t,u,v,d; 92 scanf("%d",&t); 93 while(t--){ 94 scanf("%d%d",&n,&m); 95 init(); 96 for(int i=0;i<m;i++){ 97 scanf("%d%d%s",&u,&v,s); 98 in[v]++,out[u]++; 99 if(s[0]=='U'){ 100 addu(u,v,sn); 101 addE(u,v,1); 102 } 103 else ok[u][v]++; 104 } 105 int flag=1,sum1=0,sum2=0; 106 for(int i=1;i<=n;i++){ 107 if(in[i]==out[i]) continue; 108 if((in[i]-out[i])&1){ 109 flag=0; 110 break; 111 } 112 else if(out[i]>in[i]){ 113 sum1+=(out[i]-in[i])/2; 114 addE(sb,i,(out[i]-in[i])/2); 115 } 116 else{ 117 sum2+=(in[i]-out[i])/2; 118 addE(i,se,(in[i]-out[i])/2); 119 } 120 } 121 if(!flag||sum1!=sum2||dinic()!=sum1) printf("No euler circuit exist "); 122 else{ 123 for(int i=1;i<=n;i++){ 124 cur[i]=1; 125 for(int j=headu[i];~j;j=U[j].ne){ 126 if(S[U[j].w].w>0) ok[i][U[j].v]++; 127 else ok[U[j].v][i]++; 128 } 129 } 130 cnt=0; 131 dfs2(1); 132 for(int i=cnt-1;i>=0;i--) printf("%d%c",ans[i]," "[i==0]); 133 } 134 printf(" "); 135 } 136 return 0; 137 }
