0. Introduction
- ML的RoadMap
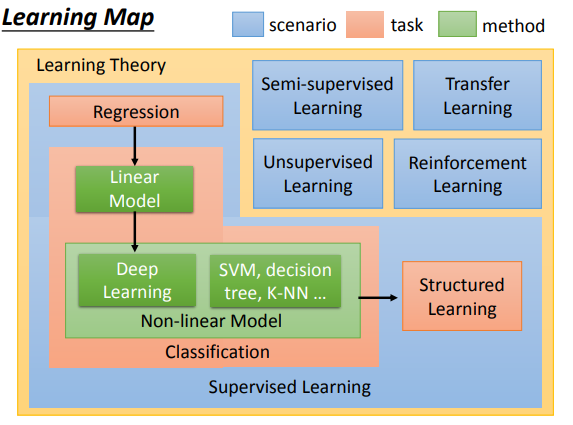
-
Regression问题中的Errot :Where does the error
come from?
一种解释:Errot = bias + variance 【偏差+方差】 -
所以,如果能做出:Bias and Variance of Estimator,也就可以量化Error
sample N examples:
有两个公式:求E & D [简单的概率公式]
结论:如果bias较大,可能是underfitting, 需要提高model complexity,加入更power的feature;如果variance较大,可能是overfitting,需要降低model complexity,加入regularization -
model select and test
train-->test
train+vilidation(model selection)-->test
k-fold validation
1. Gradient Descent:
1.1 基本公式:w_t = w_t - learning_rate*grad(w_(t-1))
1.2 learning_rate的类别:
- 记grad(w_(t-1))为g(t-1)
- vanila gd:
- yita_t = yita_0/sqrt(t+1)
- 这个rate的来源:想要达到一个效果:optimiqaztion的初始阶段大步前进,到了快要接近最优解的局部,就小步尝试。所以从直观上看,理想的rate应该随着时间递减。而sqrt又是可微分的,所以选这个公式。
- Adaptive gd:
- yita_t = yita_0/sqrt(t+1)
- theta_t = sqrt(||g||^2 / (t+1))
- learning_rate = yita_t/theta_t = yita_0/sqrt(||g||^2)
- 这个learning rate的来源:通过一个对二次函数做optimization这个特例中得到的猜想,以及做一个近似。【没有严格证明】
1.3 一个Faster的GD:SGD
- 核心思想:不操作所有点,只是有策略地选取一个点做GD
- 公式:
1.4 证明GD的正确性:
- 引入Feature Scaling:就是本科的对统计变量做标准化,比如正态分布的点做标准化
- 证明目标:[我们每次更新完的新的w总能使L(w)一直在递减],即L(w_{t+1}) < L(w_{t})恒成立
- 证明策略:在局部(w)领域内对L(w)做高维的泰勒一次函数展开,将L(w)的最小化问题转化为一个【两个向量做内积】的式子,而两个向量内积最小发生在:两个向量方向恰相反的情况下。据此得出w的闭式解。这就是GD的公式
- 注:对L(w)做高维的二次函数展开,就能推导得到【牛顿法做optimization】的公式
1.5 一个折中的GD:minibatch GD:
- 核心思想:不是选取所有点,也不是只选一个点,而是有策略的选取一部分点做GD
- 公式:
1.6 GD的局限性:[可参考李宏毅的PDF]
- very slow at plateau
- stuck at saddle point
- stuck at local minima
- 注:后期有时间要参考下convex optimization,看下GD的各种变种。
- 注:我记得仿生算法【遗传,蚁群,粒子群,等】似乎就是应对GD这些局限性而提出来的一些optimization algorithm
2. Regression
- loss func 是 均方误差
(loss = frac{1}{2m}sum_{i=1}^m(y_i-hat{y_i})^2)
3. Classification
3.1 view:
Classification as a special type of Regression
3.2 Probabilistic Generative Model for Classification
-
最开始,引入贝叶斯求解后验概率,利用这个后验概率与阈值比较划分类别。【二分类问题】
- Function Set:

- 注:【(p(x|C_i)由高斯分布求得,p(C_i)由古典概型求得),这两者均是先验概率,可以通过({train-set: (x,y)})求出来】

- Function Set:
-
首先他是假设(x,y)采样自一个高斯。两堆(x,y)就是两个不同的高斯.
- 他的想法是,一旦确定了两个高斯,那么就能分别回归这两堆数据。回归的结果后面套一个【回归值与阈值的比较判别器】,Regression就变成Classification
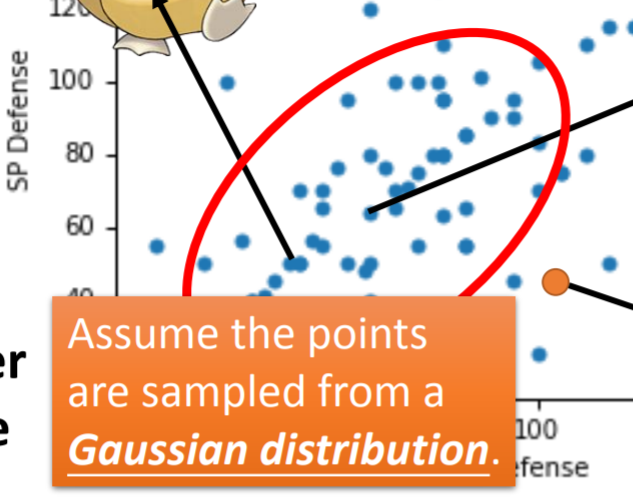
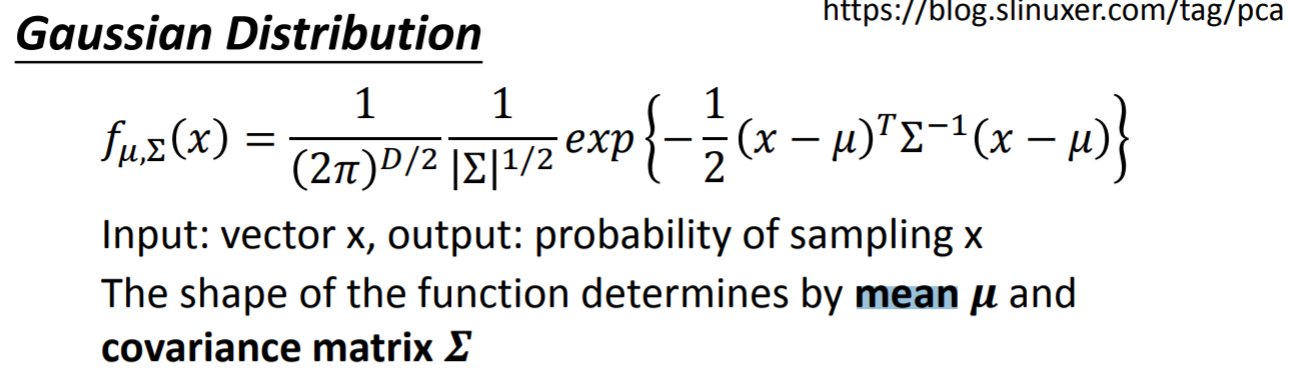

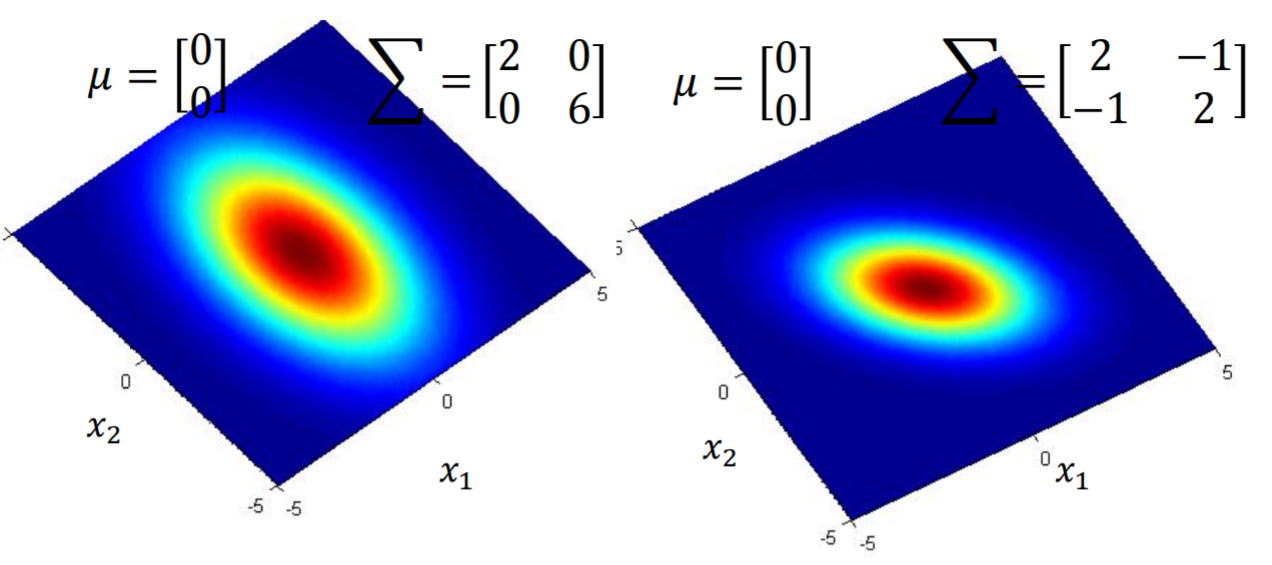
-
use MaxLikeliHood来求解这两个高斯的参数【即利用Maxlikelihood做参数估计,这是大学概率的内容了】
-
举例:
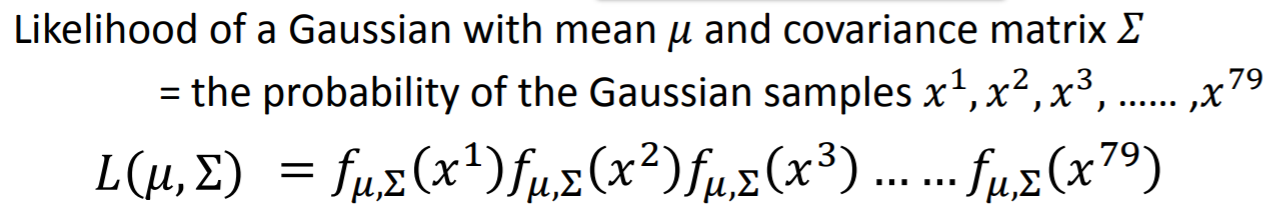
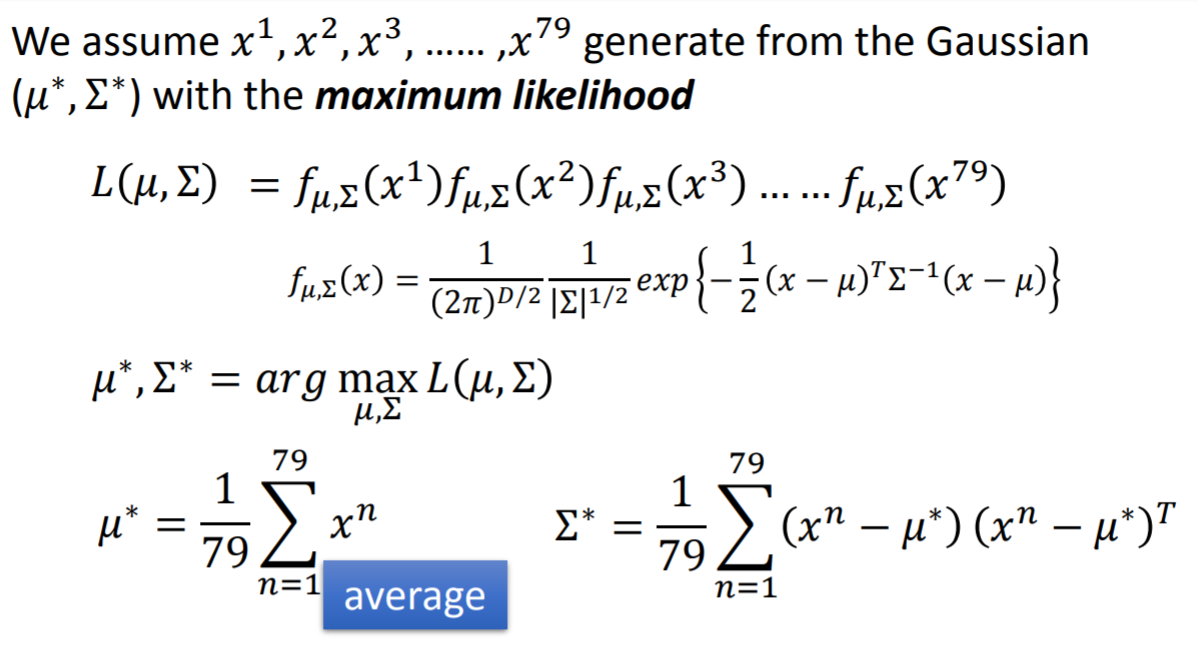
-
注:上述 (u^*,sigma^*)是由 (max L(mu^*,sigma^*))优化得到,过程很简单,故略
-
利用这个得到的高斯,可以预测下eval-set数据点x属于哪个label,求(E_{eval});也可以对之前的train-set做一个检验,看下(E_{train})

-
-
做一些改进,及其对应的(E_{eval}):
- two class have mu_1, sigma_1 and mu_2, sigma_2 :<40% accuracy in the test data
- use more feature : 54% [2-dim x --> 6-dim x]
- two class have mu_1, mu_2 , share_same sigma_same : 60%
- use more feature : 74%
-
overview the process:
-
Function Set【Model】 : 基于贝叶斯的后验概率,这是分类器的核心
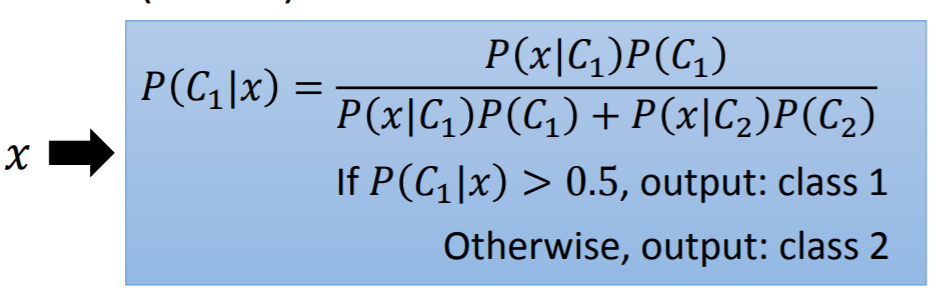
-
Goodness of a function【Loss func】: assume x sampled from Guassian distubution and iid., we get L(mu,sigma)
-
Find the best function【opitimization】:we want to try the optimal mu_* and siama_* to maxima the LikeliHood,即最大化L(mu,sigma)
-
-
一些经验:
-
if you assume all the features are independent, then you are using Naive Bayes Classifier,这个NBC的本质是:【把针对高维属性的高维Guassian简化为一维Guassian的连乘,每一个一维guassian处理x的一个feature】

-
如上图所述,for binary features, you may assume the are from Bernoulli distributions 【即简化Guassian为Bernoulli】,如何简化,后面找例子再详述。
-
-
改进分类器的判别公式,寻找它与之前的Regression公式的联系
-
改进(p(C_i|x))

-
再次改进(z)的结构

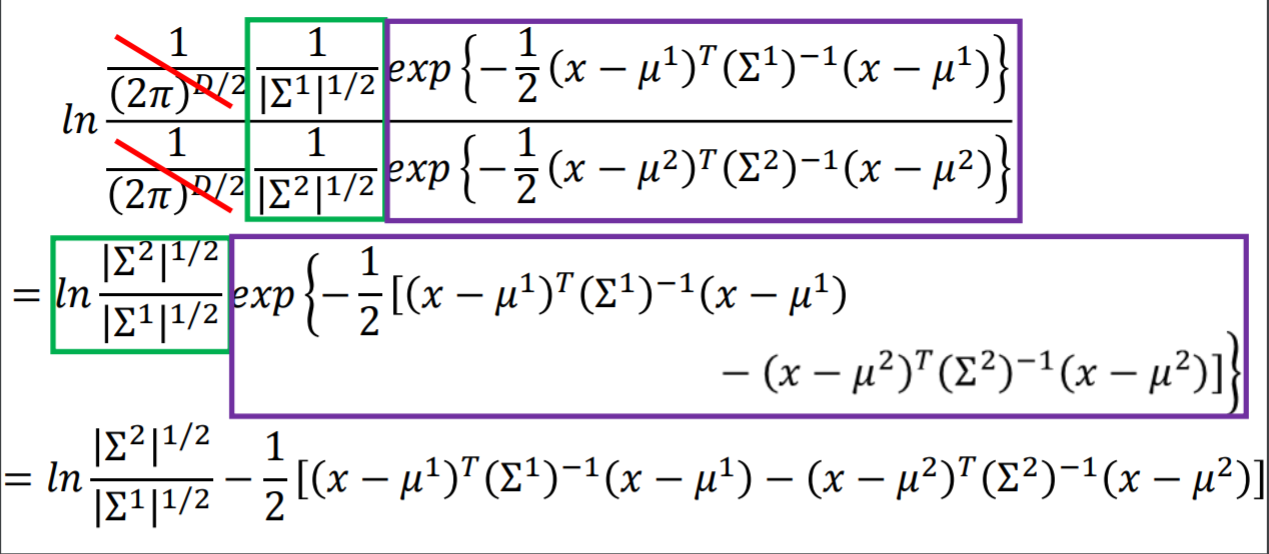
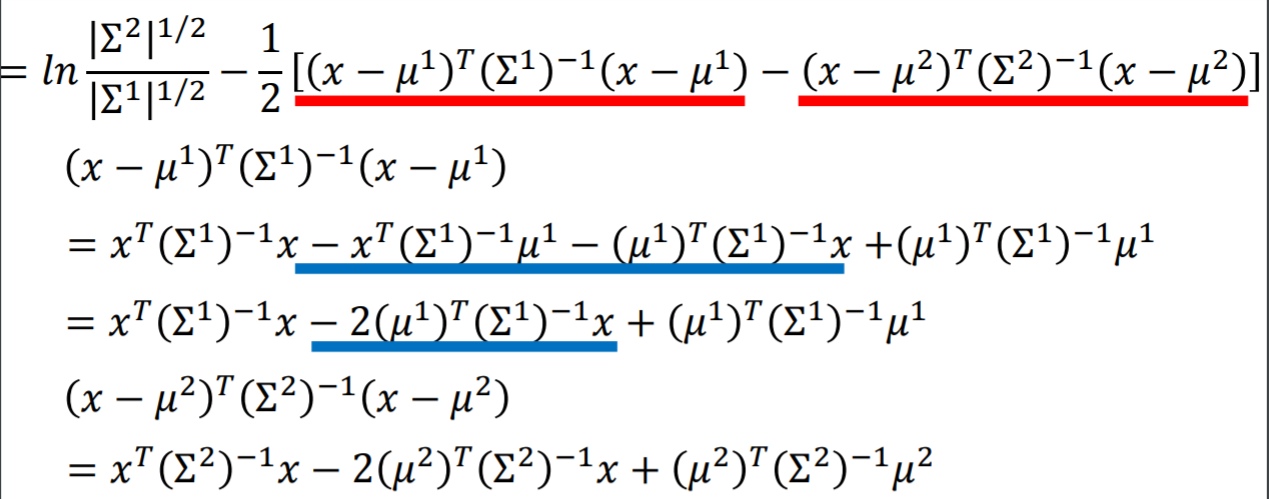
- 注:上图中红线到蓝线的展开,等价于一个带系数((sigma^1)^{-1})的平方展开【系数始终放在中间】,向量运算与实数结构是相似的。要用这种直觉去看待向量运算。
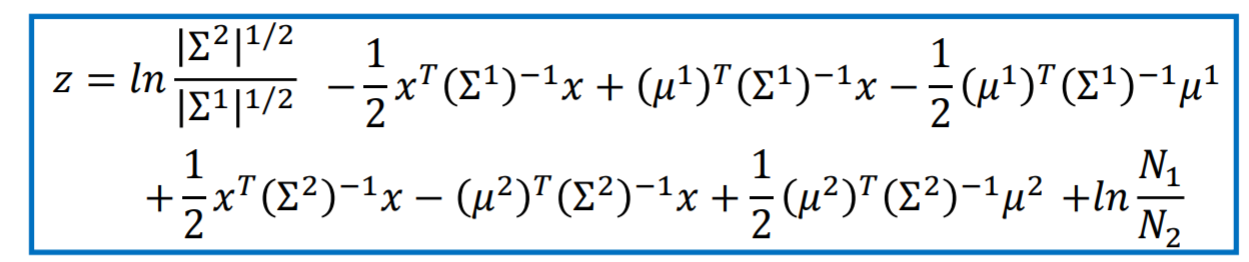
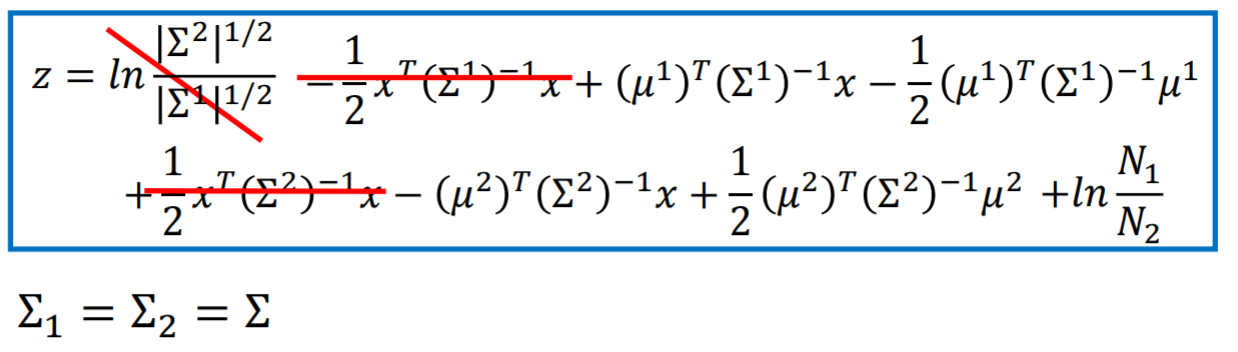
-
注: 上图中(sigma^1 == sigma^2) 起到了简化计算的效果。【后面自己造公式也要考虑类似近似技巧,只要这个近似有相对可靠的理论支撑】
-
重新换元变形得:

-
观察发现,这个基于贝叶斯后验概率的Classification的function set最终的结构和之前的Linear Regression竟然完全一致!【这个现象的本质是因为:我们Classification的公式变形中,加入了一个假设:两个高斯的(sigma)相同】
-
而非常巧合的是,这个model的针对【已知train-set】求最大似然的loss func和【从信息论角度推导的cross entropy对应产生的loss func】是完全一致的!下面一个章节将会讨论如何从信息论的角度推导出衡量【最小化两个概率分布的"距离"度量的工具】,即cross entropy,进而基于CE的分类器model。
-
-
总结下上述推导:
- p_{mu,sigma} = theta(z) 【此处恰好theta(z) = sigmod(z)】
- z = w*x +b 【恰好能凑出这个结构】
- 根据p_{mu,sigma}与classification的threshold,就可以判定当前属于哪一个类别
- 从上述推导的视角看,Classification就是:先做了一步Regression(z = w*x+b),然后又做了一步theta(z)。从而间接证明了Classification就是一种特殊的Regression.
-
上述model的本质:
- 首先根据贝叶斯条件概率推导出【基于后验概率的分类公式】;然后假设两类样本点均服从高斯分布,仅高斯参数不同;然后基于【生成这些样本点的概率】定义似然函数,根据MaxlikeliHood求解两个高斯的参数;最后参数调整代入【后验概率公式】,得到最终的分类公式。
- 牢记这个model做的若干假设:1,train-set的(p(x|C_i))服从高斯分布;2,高维属性直接独立,所以可使用Naive-Byes简化求解(P(x|C_i));3,假设两个高斯的(sigma)是相同的;
- 本质:是假设了两个分布,然后再“合并”两个分布,【推导得到最终的分类公式】。
- 这是一种Probabilistic Generative Model。【分类公式的最终结构是依据概率模型,推导得到】
- 下一节即将用到的Logicstic Regression是一种Discriminative Model 【直接给出分类公式的最终结构,Function Set后面无须再推导,后面只需要确定参数即可,无须再推导了】
3.3 Logistic Regresion 【Discriminative Model】
3.3.1 LR的过程【过程的结构与上一节相同】:
-
Function Set:

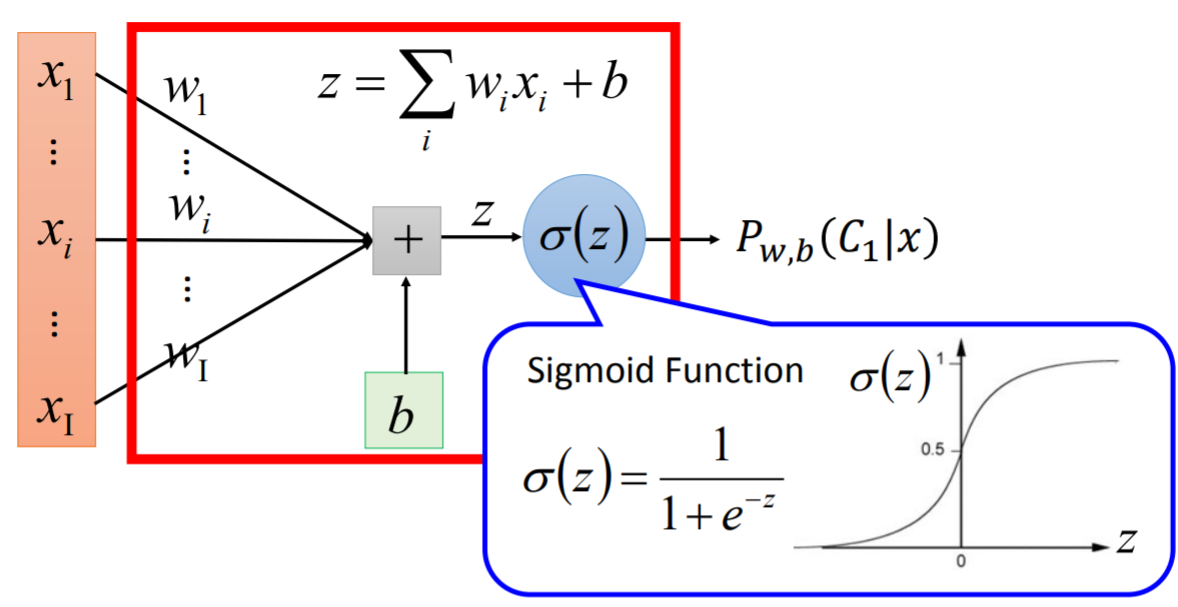
-
Goodness of a Function:【原理还是根据“生成这些数据”的似然函数】


- 注:如上图,对max 加log不改变单调性,max取负变为求min是做优化的最常见的套路。最终得到loss func,如下:
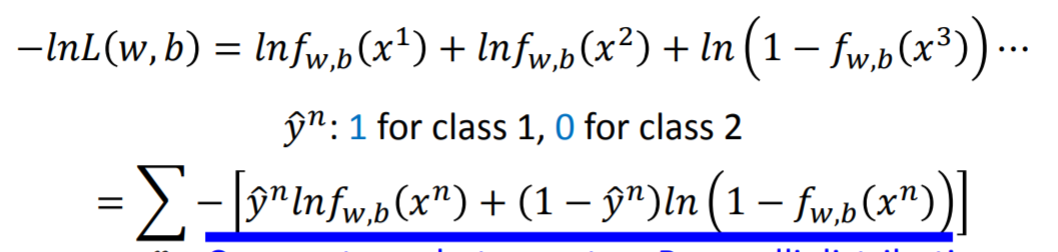
- 注:添加0-1指示变量来统一公式,也是一个最常见的数学技巧。
- 并且,这个loss func的推导不仅能从上述的【maxlikelihood】得来,还可以直接由Cross Entropy得到,下一节开始介绍CE。
-
Find the best function:【这个放在3.3.3中再详细交代】
3.3.2 Cross-Entropy
-
信息量:
- (I(x_0)=-log(p(x_0)))
- 直观的物理含义:某个事件发生的概率越大【即(p(x=x_{0}))接近1】,它对应的信息量就越小。
- 直观的例子解释:概率大的事件发生的可能性大,所以无法带给人更多的收获和反差【比如{太阳东升西落}这个事件没有什么信息量】。而【太阳东落西升】这个事件是低概率事件竟然发生了,给人极大反差和很多意外的收获,信息量较大。再说简单点:概率大的事情大家都知道,是不稀缺的,信息价值低;小概率事件是稀缺的,物以稀为贵,信息价值大。
- 如图:
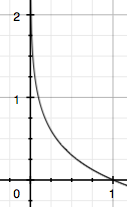
横轴是(p(x)),纵轴是(I(x)),这个曲线符合我们的物理直觉。
-
信息熵:
记{小米的考试成绩为x},x有两个取值:(x_0, x_1 ; and ; x_0 + x_1 = 1 ),那么如何度量x的不确定性呢?答:对x的不同取值所包含的信息量求期望:(H(x)=-[p(x_0)log(p(x_0))+(1-p(x_0))log(1-p(x_0))])
熵越大,不确定性越大,越不稳定,总信息量大;反之稳定,总信息量小。【实现了熵与信息量之间的某种正向关系】
- 定义离散型变量x的信息熵Entropy
(H(X)=E_plog frac{1}{p(x)}=-sumlimits_{x∈X}p(x)log p(x)) - 连续型x:
(H(X)=-intlimits_{x∈X}p(x)log p(x)dx) - 为了确保连续性,约定:(p(x) ightarrow 0时,有p(x)log p(x) ightarrow 0)
- 可以做出(x={0,1}时,H(p)与P的关系图):

当(p=0.5)时,不确定性最大,对应的信息量也最大,同时信息熵也最大。注:此处默认熵的log底数为2
- 相对熵:
相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x),我们可以使用 KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异。
In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.
即如果用P来描述目标问题,而不是用Q来描述目标问题,得到的信息增量。一个直观的解释:真实的分布P是未知的,而我们的model假设的分布Q的信息量不足,需要一些信息增益才足以逼近P。
- 交叉熵
上述公式最后一项就是cross entropy交叉熵:
(H(p,q)=-sum_{i=1}^np(x_i)log(q(x_i)))
- 一个直观而有趣的信息论解释:[来自于下面的知乎链接]
熵是什么?设p是一个分布, (-p*log(p))表示该种概率分布的熵,而(-log(p))表示编码的长度。所以熵就是最小的平均编码长度。交叉熵,就是用一种分布q去近似未知的分布p,那如何评价你选的分布q的好坏呢?就用你选定的q去编码分布p,然后得出的编码长度最小就表明你选择的分布q是很好的。
牢记一个概念:我们下面的label仅仅只是train-set,而predicts是我们的model得到的【我们现在讨论的是如何确保model假设的Q分布如何逼近train-set的P分布;暂时没有讨论train-set和test-set如何逼近的问题。】
在机器学习中,我们需要评估label和predicts之间的差距,使用KL散度刚刚好,即DKL(y||y^),由于KL散度中的前一部分−H(y)不变【因为这里的y是指来自于train-set,一旦选定y,对应的H(p)就是常数】,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss,评估模型。
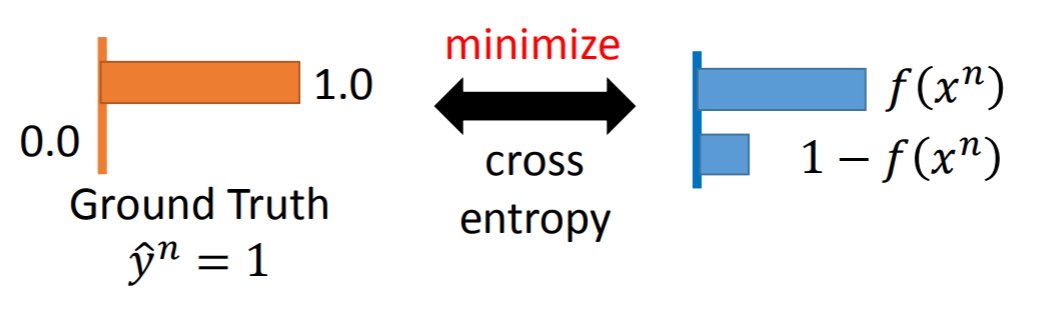
- 注:李宏毅这个教程有个很坑爹的地方:颠倒了大家【习惯把y作为true label,y^作为model的predict label的习惯】,需要时刻提醒自己,他此处的notion恰好与约定俗成反过来了。
- 处理Binary Classificartion【近似于Logistic Regression】时,CE的应用:
把上述CE中的P,Q替换成train-set的true_label y{y要么为0,要么为1这两个概率值}及我们model的predict_lable y^ {y^由之前的铺垫可知是一个0到1之间的概率值},就相当于最小化这两个概率值的“差距”:
有趣的是,上一节我们利用【Maxlikelihood最后得到的loss func也是这个,从信息论的CE角度出发及从最大似然估计角度出发,两者求的loss竟然是相同的,奇妙!】
6. 处理多分类问题: 我们由上已知:在二分类问题中,CE作为loss,而这个loss也可以由【假设train-set每个样本点服从{以我们假设的model的输出,为参数的伯努利分布}做最大似然估计】得来。其实多分类问题的CE本质上也对应地为【假设train-set的每个样本点服从以{model输出,为参数的多项分布}的极大似然估计】。而应对回归问题时,L_1 Loss和 L_2 Loss均可用极大似然估计法推得, L_1 和 L_2 正则化项则可以通过贝叶斯估计中的最大后验概率估计推得【这事后面我要TODO,手推公式验证下】。
7. CE的使用要注意:
- true label和predict label均要转为概率值【比如NN中,输入的复杂feature可以被转化为one-shot编码,输出要经过一层softmax才能,进行下一步的计算CE】
- true和predict接近时,CE越小。【这一点,CE有“距离”的特点】
- CE(A,B)!=CE(B,A),这一点切记!CE不满足交换律
8. 参考:
- https://blog.csdn.net/rtygbwwwerr/article/details/50778098
- https://en.wikipedia.org/wiki/Cross_entropy 【这个链接的Cross-entropy error function and logistic regression 处,对上一个链接进行补充说明】
- https://blog.csdn.net/tsyccnh/article/details/79163834 【讲解的套路同上,但是更加清楚/简洁/易懂;但是最后一部分{机器学习中交叉熵的应用}我猜测意思是:他说的其实是一张图片识别单个object和多object时,对loss有不同的定义】
- https://www.zhihu.com/question/65288314/answer/244557337 【大白话CE的来龙去脉】
- https://www.zhihu.com/question/65288314/answer/229748050 【对CE的一个简单物理直觉】
- https://www.zhihu.com/question/65288314/answer/230209104 [提供了对CE在实践中的本质理解]
- https://www.zhihu.com/question/65288314/answer/244601417 【从最大化似然函数的角度也能推导出Loss就是CE】
3.3.3 Find best func/model {其实就是找(w^* and b^*)}
- 由上得到的Loss func:

我们需要拿Loss func对w,b求微分,得到的微分值就是相应w,b的更新方向。更新方向乘以学习率就是delta w和 delta b【w,b下一轮迭代应该被更新的值】--[这也就是最开始讲到的GD]
-
计算第一项w

-
计算第二项 【这里应该是lhy打错了,(x)应换成(x^n)】

-
两项汇总,得到w的更新方向【乘以学习率就是w的更新量】
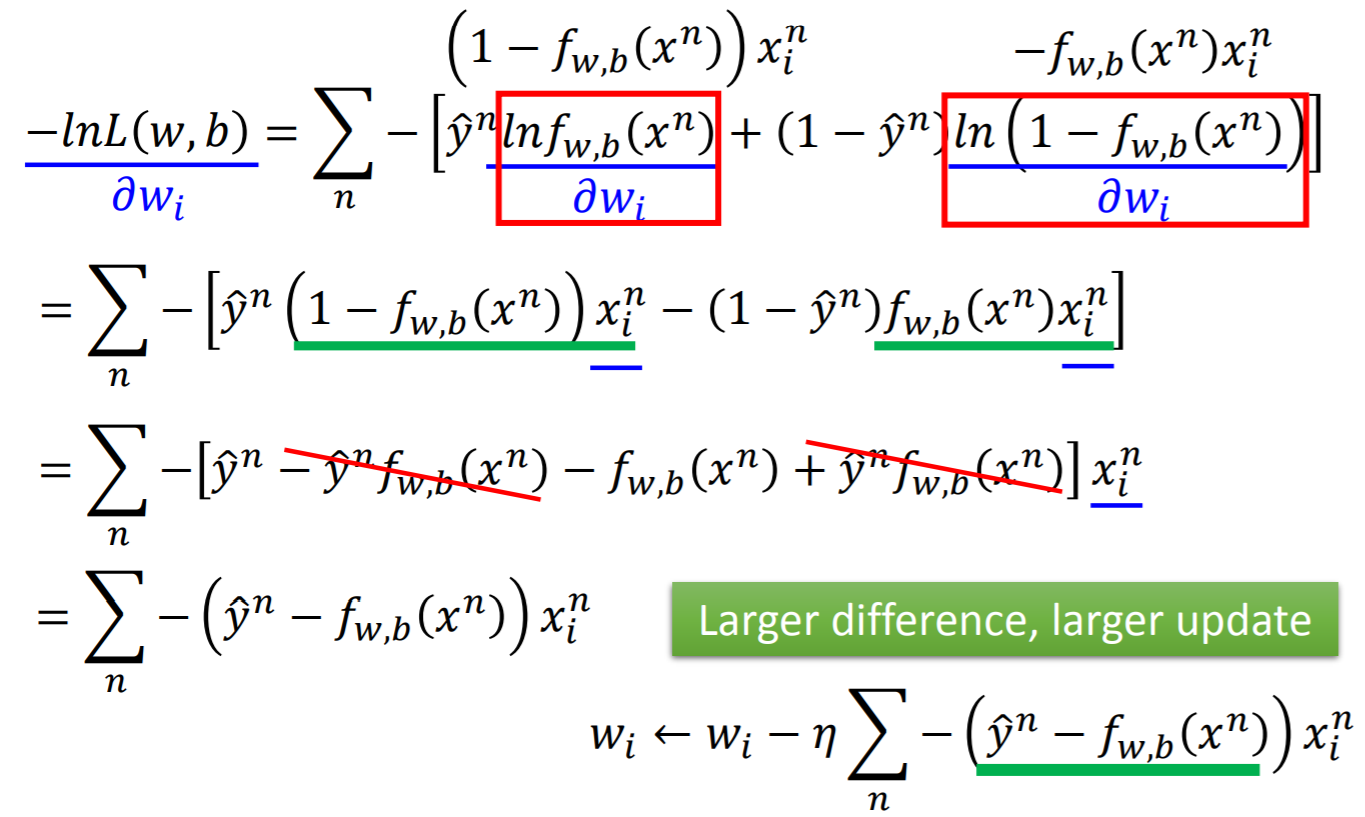
-
这个更新量同时也表达一个信息:(作为label的y^n与model计算的y差距越大,w的更新量越大)。而这也恰符合我们的直觉【你错的越多,改正应该越大】
-
后续的优化,也就是不断更新w,b来减小loss,直至达到一个可以接受的loss停止优化。得到最终的(w^*,b^*)
3.3.3 小结:
上述1-2的全过程是:(LogicRegre + Cross etropy) 【用CE作为loss func】。其实还有一个更简单的loss func:squard-error
3.3.4 考虑squard-error作为loss func的Logistic Regression
-
算法流程:
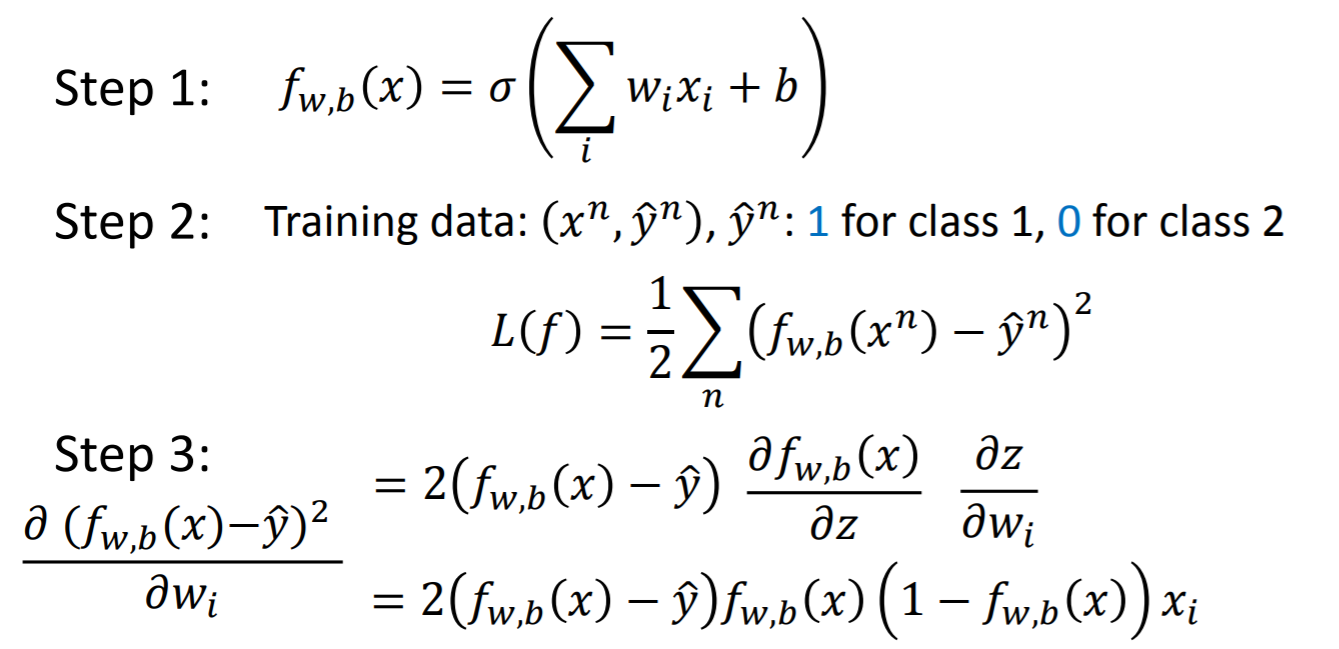
【注:lhy的step3又把(y,x)的上标n写丢了,在lhy的ppt里面,上标n代表样本集(x)中第n个样本((x^n,y^n))】 -
【CE及squard-error两者的】w的更新量均存在的现象:


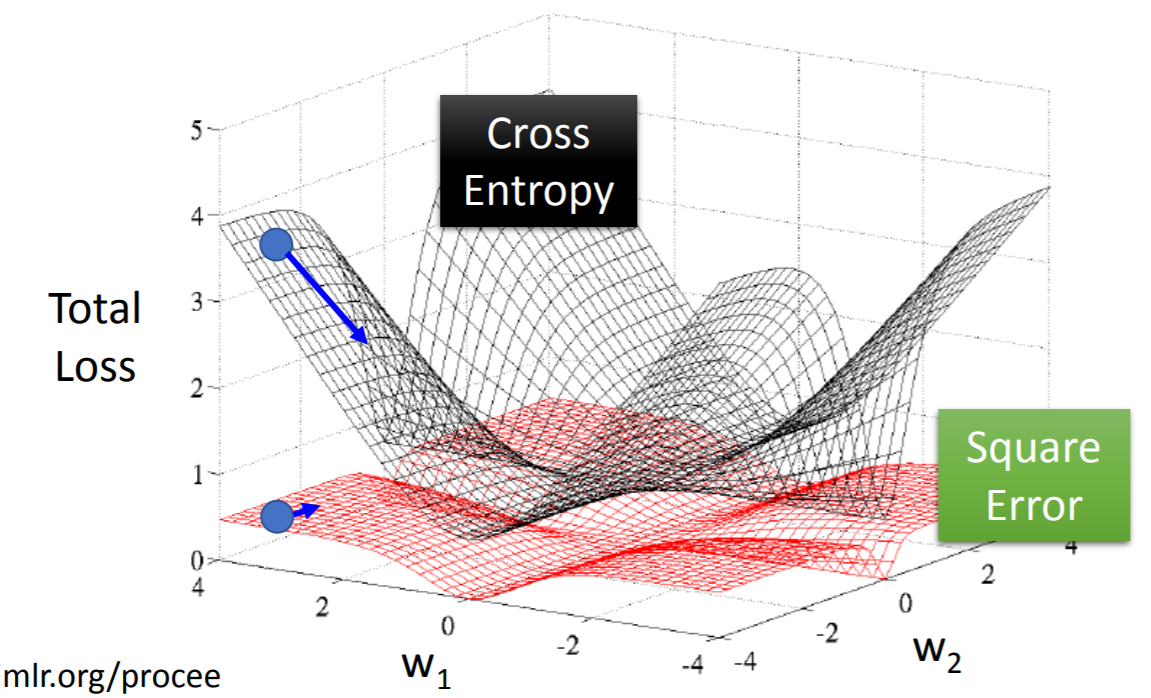
-
注:从上图看,squard-error相比ce,“坡度很平”,所以优化的过程很缓慢,甚至会“停滞不前”,导致很难得到optimal solution。所以优先使用CE作为loss func【优化过程会顺利很多】
3.3.5 Logistic Regression vs. Linear Regression


3.4 Discriminative v.s. Generative 【两类model】
-
Generative Model 需要做若干假设,然后推导出一个function set,求解参数后才能得到最终的分类器;而Discriminative Model直接定义了一个function set,后续只要求解参数即可。

-
另一个Generative的特点【或者说缺点】

上述例子中,一个样本点有两个feature,分类器把test-sample误判为class2。原因在于:Generative Model 会做一个【各属性间互相独立的假设来简化计算(p(x|C_{i}))】。这就有可能破坏了属性间存在的关联关系,导致后面产生误判。【当然,这也有可能不是误判】 -
一些关于Discriminative与Generative的观点:
- Usually people believe discriminative model is
better 【not always】 - Benefit of generative model
- With the assumption of probability distribution
- less training data is needed 【因为有若干模型假设,可以脑补一些东西,就不需要大量数据来推演】
- more robust to the noise 【因为有一些模型假设,可以对抗某些是noise的train-set】
- Priors and class-dependent probabilities can be estimated from different sources. 【比如语音识别和文本识别中(P(c_i))可以早于(P(x|c_i))之前就计算好】
- With the assumption of probability distribution
3.4 Multi-class Classification (3 classes as example)
-
对输入归一化:softmax

- 注:首先要定义三个子分类器的w,b;然后做feature transoform;再通过softmax做归一化【我在想,为什么是softmax,其他选择有没有,有什么差异?这是TODO的工作,谷歌查之】
-
基于CE定义loss func

- 注:首先根据【向量z输入到softmax】得到一个概率值向量y【(y_i)对应着三个class】;然后基于真实train-dataset的类别y^ 【这也是一个概率值向量。它根据x^ 属于三个class的不同,有三种取值,如上图】;基于y^ 与y计算CE,来作为loss func。
- 终于在这里明白了https://blog.csdn.net/tsyccnh/article/details/79163834中【CE在多分类中的应用】了。其实CE的功能就是:比较两个概率的相似度。【以此为loss func】
3.5 解决Linear Model的限制:non-linear feature transformation [接下来几章仅讨论DL这类的feature-transorform]
