ConcurrentHashMap
内部结构
在JDK1.8之前的实现结构是:ReentrantLock+Segment+HashEntry+链表
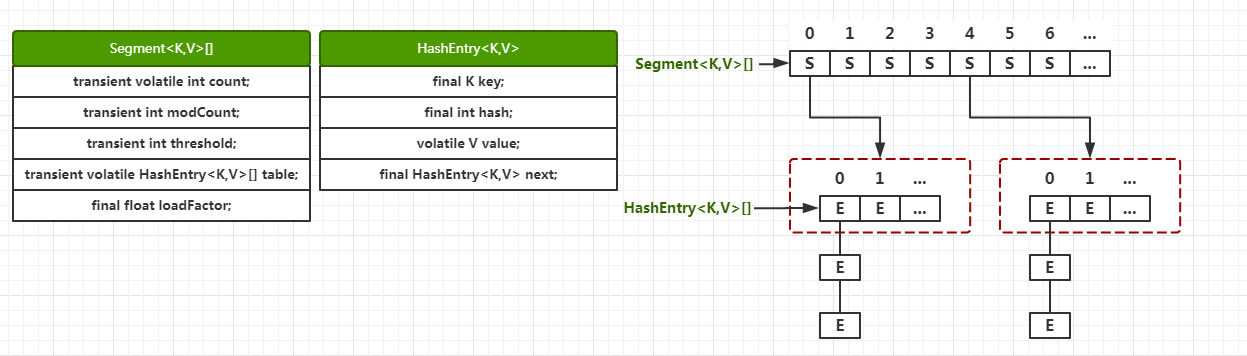
JDK1.8之后的实现结构是:synchronized+CAS+Node+链表或红黑树(与HashMap一致)
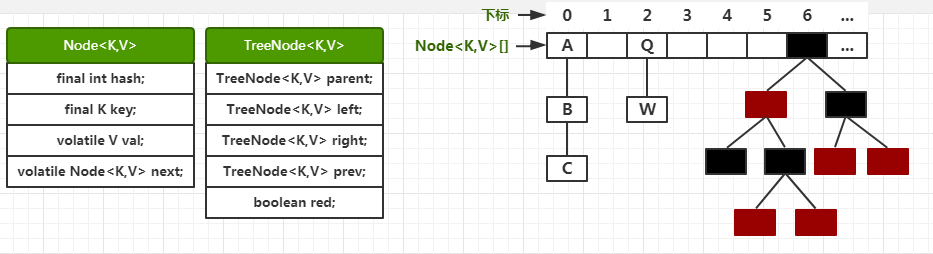
而1.8之前锁的是Segment,1.8锁的是Node数组里的Node,准确来说是头结点。如图虚线所示:
为什么要废弃锁分段机制:
1. 分段造成内存浪费(内存不连续,碎片化)
2. 在添加时竞争同一个锁的概率非常小,分段锁反而会造成更新等操作的长时间等待;并且当某个段很大时,分段锁的性能会下降。
3. 为了提高 GC 的效率
为什么加锁不用ReentrantLock而是用synchronized:
1. 锁的细化,之前ReentrantLock锁住的是整个段,现在synchronized锁住的是单个Node。
2. 因为锁的细化,出现竞争的情况大大减少。
3. 如果竞争同一个Node,只要线程可以在自旋有限次数内拿到锁,Synchronized就不会升级为重量级锁,而等待的线程也就不用被挂起,我们也就少了挂起和唤醒这个上下文切换的过程开销;而ReentrantLock不会自旋,只会挂起,多了个上下文切换的开销。
为什么容量最好为2的幂:
当数组长度为2的n次幂的时候,不同的key算得hash相同的几率较小,那么数据在数组上分布就比较均匀,也就是发生碰撞的几率较小,进而导致链表结构减少,查询的时候不用遍历链表的话查询效率就高了。
为什么get不用加锁:
前面我画的图里,Node的成员变量val是用volatile关键字修饰的,其它线程做出的修改能够马上看见,保证每次读取的都是最新的数据。
源码
put
final V putVal(K key, V value, boolean onlyIfAbsent) { // key和value 不能为null if (key == null || value == null) throw new NullPointerException(); int hash = spread(key.hashCode()); int binCount = 0; // 遍历Node数组 for (Node<K,V>[] tab = table;;) { // f存储当前位置数组上的Node,n代表数组长度,i代表当前数组下标,fh代表当前Node的hash值 Node<K,V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0) // 为空或者长度为0,初始化数组 tab = initTable(); else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { // 目标位置的值为null,利用CAS设置value,返回。 if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value, null))) break; // no lock when adding to empty bin } else if ((fh = f.hash) == MOVED) // 如果hash值等于-1,代表正在扩容,helpTransfer会帮助扩容 tab = helpTransfer(tab, f); else { V oldVal = null; // 加锁进入 synchronized (f) { // 再获取一下当前位置的Node,如果和前面获取的f不一致则发生了变化,跳出同步块 if (tabAt(tab, i) == f) { // fh为正数,代表链表结构 if (fh >= 0) { binCount = 1; // 遍历链表节点 for (Node<K,V> e = f;; ++binCount) { K ek; // 如果hash值一样,并且key也一样,则覆盖旧值 if (e.hash == hash && ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; if (!onlyIfAbsent) e.val = value; break; } Node<K,V> pred = e; // 如果已经遍历到了最后(e.next==null),则直接插入到最后 if ((e = e.next) == null) { pred.next = new Node<K,V>(hash, key, value, null); break; } } } // fh < 0代表正在扩容或者红黑树结构 else if (f instanceof TreeBin) { Node<K,V> p; binCount = 2; // 添加到红黑树中 if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key, value)) != null) { oldVal = p.val; // key冲突,则覆盖旧值 if (!onlyIfAbsent) p.val = value; } } } } // binCount为当前位置包含的的Node数量,如果不是0,则判断是否需要扩容 if (binCount != 0) { // Node数量大于等于8,当前位置的数据类型转为树 if (binCount >= TREEIFY_THRESHOLD) treeifyBin(tab, i); // 如果oldVal不为空,证明存在覆盖的情况,直接返回旧值 if (oldVal != null) return oldVal; break; } } } // 整个Map的Node数量+1,如果需要扩容则进行扩容 addCount(1L, binCount); return null; }
过程和HashMap类似:
0. Node数组没有初始化先去初始化;
1. 根据hash找到数组中的位置,如果此位置为空,则直接利用CAS将新节点放在此处;
2. 如果当前位置不为空,则判断此位置的Node的hash是否等于-1,等于-1代表正在进行扩容操作,调用helpTransfer协助扩容;
3. 此位置Node的hash不等于-1,则对其进行加锁:
4. 如果此位置Node的hash大于等于0,证明这是个链表结构,先看是否存在相同的key,有则覆盖,无则把新结点添加到链表最后;
5. 否则判断当前节点是否是树节点,如果是树节点,则添加到树中,有重复的key同样会覆盖;
6. 退出同步块,判断binCount(Node计数器)如果大于等于8,则把当前位置的链表转变成红黑树;(这里可以看出,binCount主要服务于链表结构,具体位置统计当前链表的大小)
7. 最后把整个Map的Node总数+1,如果需要扩容则扩容。
下面看一下initTable【初始化的过程】
private final Node<K,V>[] initTable() { Node<K,V>[] tab; int sc; while ((tab = table) == null || tab.length == 0) { // table为空并且sizeCtl < 0,有其它线程在初始化,则调用Thread.yield(),让掉自己的CPU执行时间 if ((sc = sizeCtl) < 0) // 不扩容时:sizeCtl=数组长度*扩容因子;扩容和初始化table时:sizeCtl < 0 Thread.yield(); // 放弃初始化的竞争,仅仅自旋 else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) { // sizeCtl > 0,说明没有线程竞争初始化table,利用CAS将sizeCtl设置为-1,代表正在初始化 try { // 再次判断table是否为空 if ((tab = table) == null || tab.length == 0) { // 设置table容量,如果sc大于0则使用sc,否则使用默认的16 int n = (sc > 0) ? sc : DEFAULT_CAPACITY; // 根据容量new一个Node数组 @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n]; // 新数组替换老数组 table = tab = nt; // sc = 新容量 - (新容量/2^2),无符号右移2位,相当于除以2^2=4 // 以16为例:sc = 16-(16/4)= 16-4 = 12,也就是下一次扩容的阈值 sc = n - (n >>> 2); } } finally { // 最后,更新sizeCtl sizeCtl = sc; } break; } } // 返回新数组 return tab; }
总结:
1. 根据sizeCtl判断,如果小于0,表示正在初始化,则让出当前线程的时间片。
2. 设置sizeCtl为-1,代表正在执行初始化操作;如果sc存储的变量大于0,则新容量=sc,否则等于默认容量16;根据新容量new一个新Node数组,并更新table为新数组;更新sizeCtl为新容量的75%
再来看一下addCount【Node总数+1 & 扩容的过程】
/** * sizeCtl(-1表示table正在初始化,其他线程要让出CPU时间片;-N表示有N-1个线程正在执行扩容操作;大于0表示扩容阈值=容量*负载因子) * @param x 需要加上的数量 * @param check if <0, don't check resize, if <= 1 only check if uncontended */ private final void addCount(long x, int check) { // CounterCell:顾名思义,用于计数的格子。说白了就是用来统计table中每一个位置的Node数量。 CounterCell[] as; long b, s; // CounterCell不为null if ((as = counterCells) != null || // 或者利用CAS将baseCount更新为baseCount+1失败,就放弃对baseCount的操作 !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) { CounterCell a; long v; int m; boolean uncontended = true; if (as == null || (m = as.length - 1) < 0 || (a = as[ThreadLocalRandom.getProbe() & m]) == null || !(uncontended = U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) { fullAddCount(x, uncontended); return; } if (check <= 1) return; // 合计Node总数,其中的实现是遍历CounterCell[],累加其中的value s = sumCount(); } // check>=0,需要检查是否需要扩容 if (check >= 0) { // tab:指向table,nt:指向nextTable;n为当前table的容量,sc为当前扩容阈值 Node<K,V>[] tab, nt; int n, sc; // Node总数大于扩容阈值sizeCtl 并且 table不为空 并且 table容量小于最大容量 while (s >= (long)(sc = sizeCtl) && (tab = table) != null && (n = tab.length) < MAXIMUM_CAPACITY) { int rs = resizeStamp(n); // 如果正在扩容 if (sc < 0) { // 如果sizeCtl变化了或者扩容结束了,则跳出循环 if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 || sc == rs + MAX_RESIZERS || (nt = nextTable) == null || transferIndex <= 0) break; // 如果可以帮助扩容,那么将 sc 加 1. 表示多了一个线程在帮助扩容 if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) transfer(tab, nt); } // 如果没有扩容,将 sc 更新为负数,表示当前线程发起扩容操作 else if (U.compareAndSwapInt(this, SIZECTL, sc, (rs << RESIZE_STAMP_SHIFT) + 2)) transfer(tab, null); s = sumCount(); } } }
总结:
1. 使table的长度+1。CounterCell不为null,就使用CounterCell,否则直接利用CAS操纵baseCount。
2. 如果需要扩容,先看是否已经在扩容了,如果是,则加入扩容线程,否则就调用扩容方法开启扩容。
最后看transfer方法,这是扩容过程 的核心
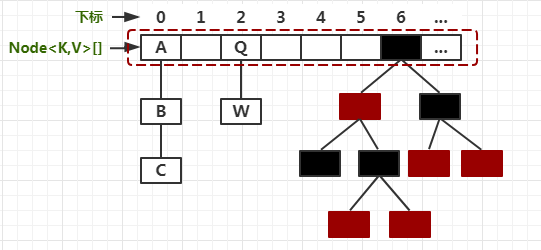
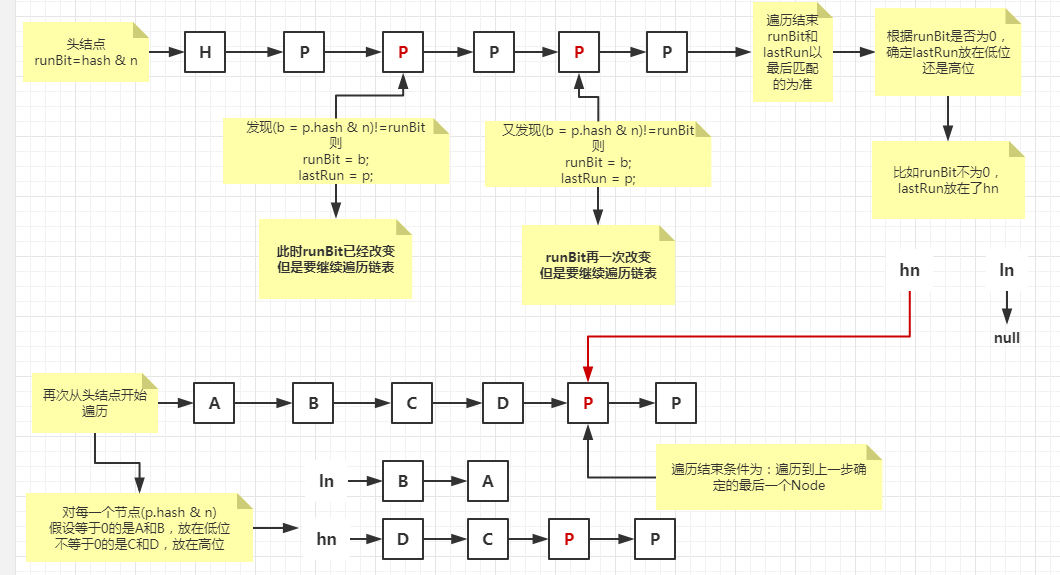
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) { // n为当前数组大小,stride存储步长 int n = tab.length, stride; // 根据cpu核数计算出步长,用于分割扩容任务,方便其余线程帮助扩容,最小为16 // 默认每个线程处理16个桶。因此,如果长度是16的时候,扩容的时候只会有一个线程扩容。 if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE) stride = MIN_TRANSFER_STRIDE; // subdivide range // 判断nextTab是否为空,nextTab是暂时存储扩容后的node的数组,第一次进入这个方法的线程才会发现nextTab为空 if (nextTab == null) { // initiating try { // 初始化nextTab,容量是tab的2倍 @SuppressWarnings("unchecked") Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1]; nextTab = nt; } catch (Throwable ex) { // try to cope with OOME sizeCtl = Integer.MAX_VALUE; return; } nextTable = nextTab; // 当前数组长度赋给transferIndex transferIndex = n; } // nextTab的大小 int nextn = nextTab.length; ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab); boolean advance = true; // finishing为true代表扩容结束 boolean finishing = false; // to ensure sweep before committing nextTab for (int i = 0, bound = 0;;) { Node<K,V> f; int fh; // 进入一个 while 循环,分配数组中一个桶的区间给线程. 从大到小进行分配。当拿到分配值后,进行 i-- 递减。这个 i 就是数组下标。 while (advance) { int nextIndex, nextBound; if (--i >= bound || finishing) advance = false; else if ((nextIndex = transferIndex) <= 0) { i = -1; advance = false; } else if (U.compareAndSwapInt (this, TRANSFERINDEX, nextIndex, nextBound = (nextIndex > stride ? nextIndex - stride : 0))) { bound = nextBound; i = nextIndex - 1; advance = false; } } if (i < 0 || i >= n || i + n >= nextn) { int sc; // 如果扩容结束 if (finishing) { // 清除临时变量 nextTable = null; // 更新table变量 table = nextTab; // 更新sizeCtl,这个等价于新容量*0.75 sizeCtl = (n << 1) - (n >>> 1); return; } // 尝试将 sc -1. 表示这个线程结束帮助扩容了 if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) { // 果 sc - 2 不等于标识符左移 16 位。如果他们相等了,说明没有线程在帮助他们扩容了。也就是说,扩容结束了。 if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT) // 不相等,说明没结束,当前线程结束方法。 return; // 如果相等,扩容结束了,更新 finising 变量 finishing = advance = true; // 再次循环检查一下整张表 i = n; // recheck before commit } } // 如果没有完成任务,且 i 对应的槽位是空,尝试 CAS 插入占位符,让 putVal 方法的线程感知。 else if ((f = tabAt(tab, i)) == null) advance = casTabAt(tab, i, null, fwd); // 如果 i 对应的槽位不是空,且有了占位符,那么该线程跳过这个槽位,处理下一个槽位。 else if ((fh = f.hash) == MOVED) advance = true; // already processed else { // 如果以上都是不是,说明这个槽位有一个实际的值。开始同步处理这个桶。 // 到这里,都还没有对桶内数据进行转移,只是计算了下标和处理区间,然后一些完成状态判断。同时,如果对应下标内没有数据或已经被占位了,就跳过了。 // 下面的处理过程和HashMap基本一样 synchronized (f) { // 再次判断当前节点是否发生了改变 if (tabAt(tab, i) == f) { // ln=lowNode=低位桶,hn=highNode=高位桶 Node<K,V> ln, hn; // 当前是链表结构 if (fh >= 0) { // 当前节点hash和老长度进行与运算 int runBit = fh & n; Node<K,V> lastRun = f; // 从当前节点的后继开始遍历 for (Node<K,V> p = f.next; p != null; p = p.next) { // 对每个节点的hash同长度进行按位与操作 int b = p.hash & n; // 如果节点的 hash 值和首节点的 hash 值按位与结果不同 if (b != runBit) { // 更新 runBit,用于下面判断 lastRun 该赋值给 ln 还是 hn。 runBit = b; // 这个 lastRun 保证后面的节点与自己的按位与值相同,避免后面没有必要的循环 lastRun = p; } } if (runBit == 0) { // 如果最后更新的 runBit 是 0 ,设置低位节点 ln = lastRun; hn = null; } else { // 否则设置高位节点 hn = lastRun; ln = null; } // 从头开始循环,目的是生成两个链表,lastRun 作为停止条件,这样做为了避免不必要的循环(lastRun 后面都是相同的hash按位与结果) for (Node<K,V> p = f; p != lastRun; p = p.next) { int ph = p.hash; K pk = p.key; V pv = p.val; // 依然根据是否为0作为区分条件 if ((ph & n) == 0) ln = new Node<K,V>(ph, pk, pv, ln); else hn = new Node<K,V>(ph, pk, pv, hn); } // 在新的数组i的位置上设置低位链表 setTabAt(nextTab, i, ln); // 在新的数组i+n的位置上设置高位链表 setTabAt(nextTab, i + n, hn); // 在老数组i的位置的链表设置成占位符 setTabAt(tab, i, fwd); // 继续向后 advance = true; } // 树结构 else if (f instanceof TreeBin) { // 当前位置的头节点,只不过是TreeNode TreeBin<K,V> t = (TreeBin<K,V>)f; // 定义低位树和高位树 TreeNode<K,V> lo = null, loTail = null; TreeNode<K,V> hi = null, hiTail = null; // 统计树的大小,为了判断是否需要退化成链表 int lc = 0, hc = 0; // 从根开始遍历 for (Node<K,V> e = t.first; e != null; e = e.next) { int h = e.hash; TreeNode<K,V> p = new TreeNode<K,V> (h, e.key, e.val, null, null); // 当前节点的hash和老长度做按位与操作,为0放在低位 if ((h & n) == 0) { if ((p.prev = loTail) == null) lo = p; else loTail.next = p; loTail = p; ++lc; } else { if ((p.prev = hiTail) == null) hi = p; else hiTail.next = p; hiTail = p; ++hc; } } // 低位达到临界值,低位退化 ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) : (hc != 0) ? new TreeBin<K,V>(lo) : t; // 高位达到临界值,高位退化 hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) : (lc != 0) ? new TreeBin<K,V>(hi) : t; // 在新的数组i的位置上设置低位树 setTabAt(nextTab, i, ln); // 在新的数组i+n的位置上设置高位链表 setTabAt(nextTab, i + n, hn); // 老数组i的位置上设置占位符 setTabAt(tab, i, fwd); // 继续向后 advance = true; } } } } } }
总体来说分为两部分:
1. 扩容前的准备和相关状态的检查
①:初始化用于存储扩容后数据的nextTable
②:分配一个桶给当前线程;判断是否扩容结束,扩容结束更新table和sizeCtl变量;判断当前桶是不是被占用了,被占用则跳过这个桶;
2. 加锁扩容
①:判断节点类型
②:如果是链表,从头结点开始遍历链表,通过当前节点和老长度的按位与操作生成一个runBit,每次遇到与前一个runBit不同的节点,则更新runBit和lastRun(当前与前面runBit不同的节点),直到遍历结束;
③:根据runBit是否为0,把lastRun节点赋给低位链表或者高位链表;
④:再次遍历链表,分割出两部分链表:以lastRun节点为停止遍历条件,根据每个Node的hash和老长度的按位与结果是否为0,把Node划分到低位链表和高位链表中。最后把低位链表和高位链表放到新数组i和i+n的位置上,老数组i的位置上设置占位符。继续处理其它剩余的桶。
⑤:处理树形结构,逻辑和链表一样,只不过多了个判断是否退化成链表的逻辑。
扩容过程我画了个图
最后设置新位置

ConcurrentSkipListMap
介绍
一个类似于树的二维链接的跳跃列表,说白了就是基于“跳表”实现的,并且它是线程安全且有序的。
跳跃表知识
跳表的原理非常简单,跳表其实就是一种可以进行二分查找的有序链表。比如:在一个使用有序链表描述的具有n个元素的字典中进行搜索,至多需进行n次比较。如果在链中部节点加一个指针,则比较次数可以减少一半。这仅仅增加了一级索引,如果增加多个呢?首先在最高级索引上查找最后一个小于当前查找元素的位置,然后再跳到次高级索引继续查找,直到跳到最底层为止。
大体结构如下,看起来像二叉树,但是比二叉树维护Balance的成本要低。
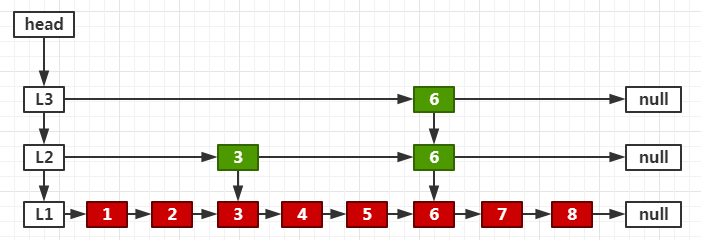
ConcurrentSkipListMap内部结构
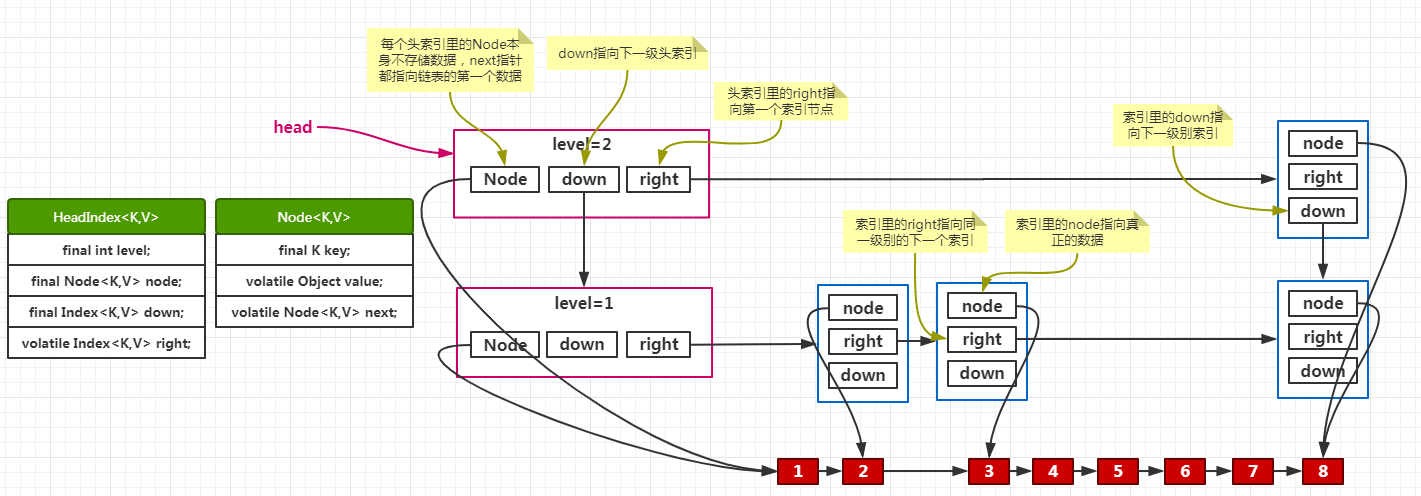
源码
先来看插入的时候,怎样去寻找位置的
private Node<K,V> findPredecessor(Object key, Comparator<? super K> cmp) { if (key == null) throw new NullPointerException(); // don't postpone errors for (;;) { // 从头索引的head开始搜索(也就是从第一层的第一个Index开始) // 这里两个变量,r代表当前要处理的Index,以及r的前驱q for (Index<K,V> q = head, r = q.right, d;;) { // 如果当前节点有数据 if (r != null) { // 当前Index里的Node Node<K,V> n = r.node; // 当前Index里的Node里的key K k = n.key; // 当前Index里的Node里的value为空 if (n.value == null) { // 如果断开q和其后继r的连接失败,则跳出内循环,然后重新开始搜索 if (!q.unlink(r)) break; // restart // 如果断开成功,则r指向下一个right,进入下一次循环 r = q.right; // reread r continue; } // 如果传入的key大于当前Index里的Node里的key if (cpr(cmp, key, k) > 0) { // 将前驱改为当前Index;然后移动到下一个同层right,从指向的Index再次比较 q = r; r = r.right; continue; } } // 如果下一层为空,则直接返回当前前驱里存储的Node if ((d = q.down) == null) return q.node; // 移动到下一层Index,前驱是当前前驱的下层Index,下次要处理的Index是当前前驱的下层Index的right q = d; r = d.right; } } }
图解过程
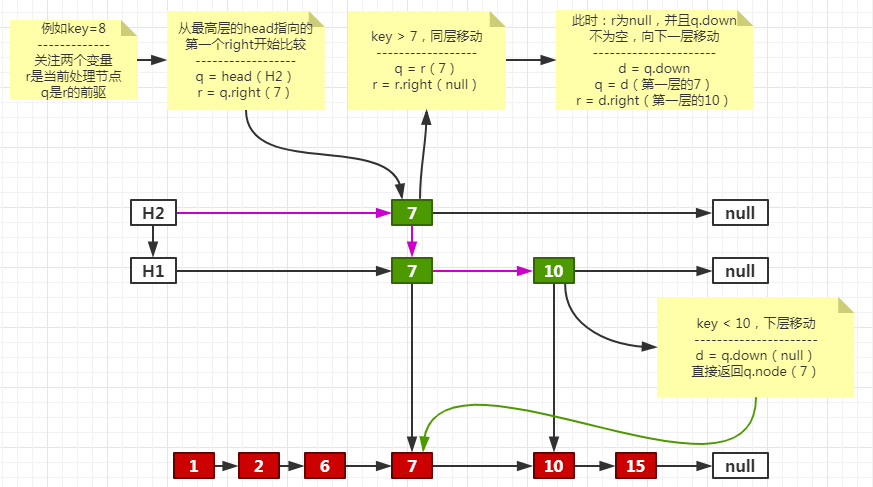
了解寻找前驱的过程后,来看doPut
private V doPut(K key, V value, boolean onlyIfAbsent) { Node<K,V> z; // added node if (key == null) throw new NullPointerException(); Comparator<? super K> cmp = comparator; outer: for (;;) { // 找到当前key的前驱(findPredecessor)和后继(b.next) for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) { // 后继不为空 if (n != null) { Object v; int c; Node<K,V> f = n.next; if (n != b.next) // inconsistent read break; if ((v = n.value) == null) { // n is deleted n.helpDelete(b, f); break; } if (b.value == null || v == n) // b is deleted break; // 虽然找到了前驱,但是不能直接连接,这里作比较的目的是排序 if ((c = cpr(cmp, key, n.key)) > 0) { b = n; n = f; continue; } if (c == 0) { if (onlyIfAbsent || n.casValue(v, value)) { @SuppressWarnings("unchecked") V vv = (V)v; return vv; } break; // restart if lost race to replace value } // else c < 0; fall through } // new一个新Node,后继为前面找到的后继 z = new Node<K,V>(key, value, n); // 利用CAS将前面找到的前驱的后继设置为新节点z,设置失败则重新循环 if (!b.casNext(n, z)) break; // restart if lost race to append to b break outer; // 成功则跳出双循环 } } // 以上代码的目的:找到key的前驱节点b及其后继b.next,然后将key封装成新Node,新Node的后继b.next,最后把新Node连接在b的后面 int rnd = ThreadLocalRandom.nextSecondarySeed(); if ((rnd & 0x80000001) == 0) { // test highest and lowest bits int level = 1, max; // rnd >>>= 1等价于rnd = rnd >>> 1; // (rnd >>>= 1) & 1,如果rnd无符号右移然后和1按位与的结果是偶数,即返回0,否则返回1(任何数 & 1,非0即1,这个操作可以用来判断奇偶) while (((rnd >>>= 1) & 1) != 0) // 随机数为奇数,level加1 ++level; // 上面计算level的过程完全是看心情 Index<K,V> idx = null; // HeadIndex的头结点 HeadIndex<K,V> h = head; // 如果上面计算的level小于当前最高level,则构建一个level大小的Index链表idx if (level <= (max = h.level)) { for (int i = 1; i <= level; ++i) // 当前索引的node等于z,down等于上一个索引idx,right为null。也就是循环过后,得到一个用down指针连接的链表。 idx = new Index<K,V>(z, idx, null); } else { // try to grow by one level // 如果计算得到的level大于目前最大level,则创建新的一层 level = max + 1; // hold in array and later pick the one to use // new一个level+1大小的索引数组 @SuppressWarnings("unchecked")Index<K,V>[] idxs = (Index<K,V>[])new Index<?,?>[level+1]; // 从下标1开始,给数组填充Index元素 for (int i = 1; i <= level; ++i) idxs[i] = idx = new Index<K,V>(z, idx, null); for (;;) { // 当前头索引 h = head; // 当前的level int oldLevel = h.level; // 数据不对头,放弃层数加1的操作 if (level <= oldLevel) break; // 新的头索引 HeadIndex<K,V> newh = h; // 头索引里对数据Node的引用 Node<K,V> oldbase = h.node; // new一个新的头索引 for (int j = oldLevel+1; j <= level; ++j) // 新的头索引的down指针指向当前头索引 // right指针指向idxs最高层的索引 // j代表当前的level newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j); // 利用CAS设置新的头索引 if (casHead(h, newh)) { // h指向新的头索引 h = newh; // idx更新为次高层的索引,此时的level为变更之前的OldLevel idx = idxs[level = oldLevel]; break; } } } // 以上代码目的:创建一个idx索引链表;如果level需要加1,则创建一个新的头索引。到此我还不知道idx的作用是什么。 // 找到插入点并进行拼接 splice: for (int insertionLevel = level;;) { // insertionLevel为次高层的level // j为最高层的level int j = h.level; // q指向新的头索引,也就是最高层的head // r为最高层head的right节点 // t是前面准备的idx for (Index<K,V> q = h, r = q.right, t = idx;;) { if (q == null || t == null) break splice; if (r != null) { // 当前节点的node Node<K,V> n = r.node; // compare before deletion check avoids needing recheck // 删除前比较检查,避免需要重新检查 int c = cpr(cmp, key, n.key); if (n.value == null) { // 断开q及其后继的连接 if (!q.unlink(r)) break; // r指向下一个right r = q.right; // 开始下一次循环 continue; } // key大于当前节点的key if (c > 0) { // 前驱设置为当前节点,当前节点指向下一个right(同层右移) q = r; r = r.right; // 开始下一次循环 continue; } } // 到这里,说明key小于等于n.key // 第一次来的时候:j大于insertionLevel一般是因为增加了层数(增加层数的情况第一次循环是不需要做连接处理的,因为那个时候idx的前驱就是头索引,后继为null);等于的情况一般是没有增加层数。 if (j == insertionLevel) { // 前驱指向当前的idx,idx指向r(也就是把idx插在了当前节点和其前驱中间) if (!q.link(r, t)) break; // 连接失败,则重新循环 if (t.node.value == null) { findNode(key); break splice; } // 自减1,因为这一层的连接已经处理完毕;如果减1之后是0,代表已经是最后一层了,连接结束。 if (--insertionLevel == 0) break splice; } // t向次高层移动,为次高层的连接做准备(这里可以看出,j和insertionLevel是保持同步的) if (--j >= insertionLevel && j < level) t = t.down; // 向下一层移动 q = q.down; r = q.right; } } } return null; }
代码很长,不过没关系,我分析了一遍主要分为三步:
1. 根据新添加的key,找到插入位置的前驱和前驱的后继Node,并把新结点Node连接在前驱和后继之间。(数据链表的修改)然后根据随机数的计算结果决定是否新建一个索引,是则执行下面的步骤:
2. 创建一个idx索引链表;如果level需要加1,则创建一个新的头索引。(主要目的是生成一个新结点的Index索引链表)
3. 把新的idx索引链表连接到当前已有的索引结构中。
第一步:寻找过程自行看上面,我已经分析过了
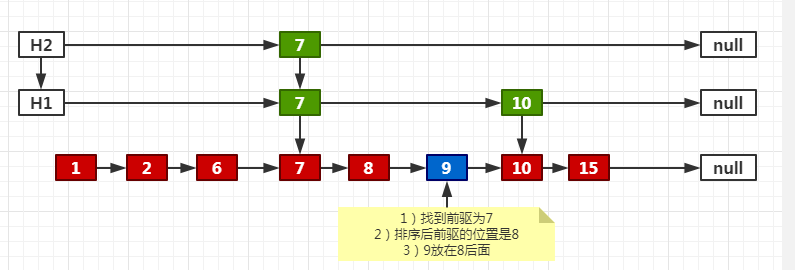
如果需要建立索引:
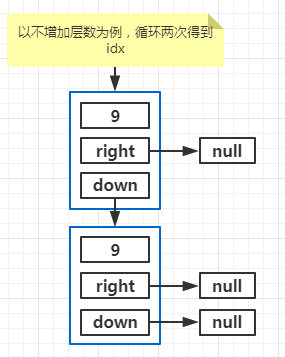
把新索引连接到已有索引结构中
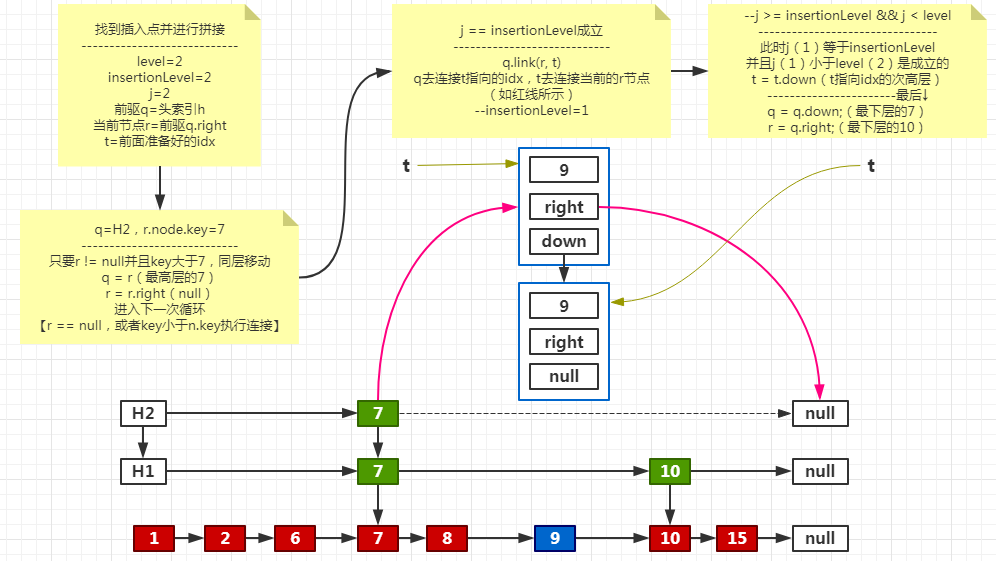
处理下一层
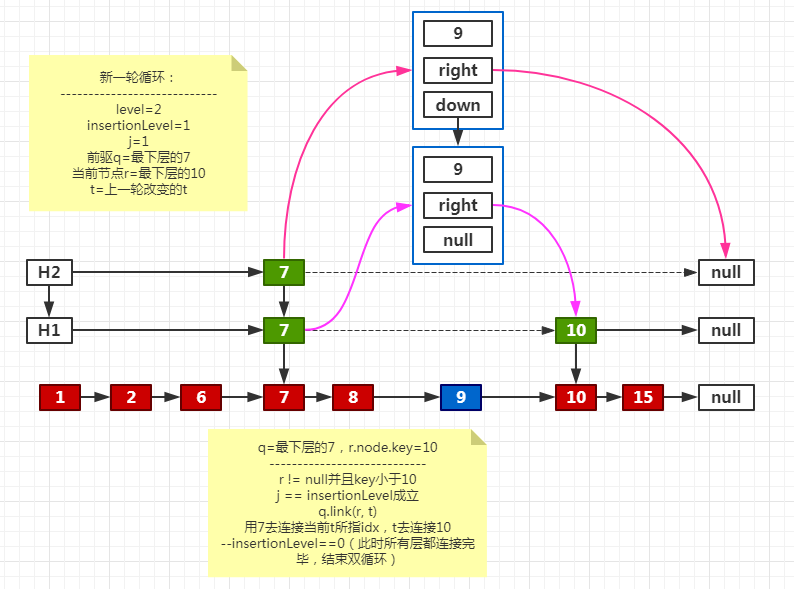
最终效果
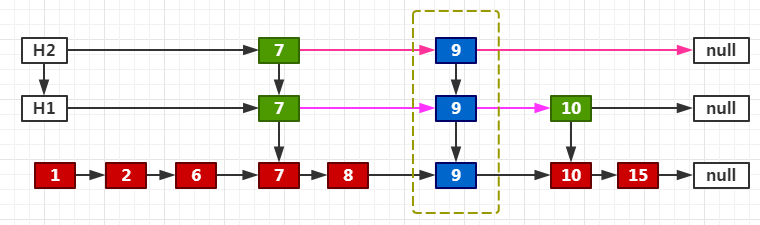
同理,如果是增加一层的情况
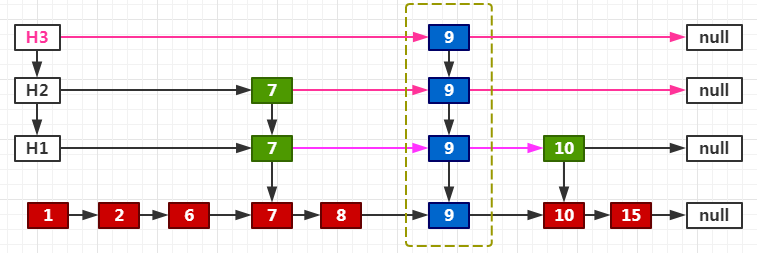
总结:为什么没有同步代码,却能线程安全?
我们看到添加Node的时候、新增HeadIndex的时候、连接新的Index的时候,都用了双循环+CAS。这就保证了竞争失败的时候,都能够退出内循环,然后重新尝试;成功即跳出外层循环。
再来看删除
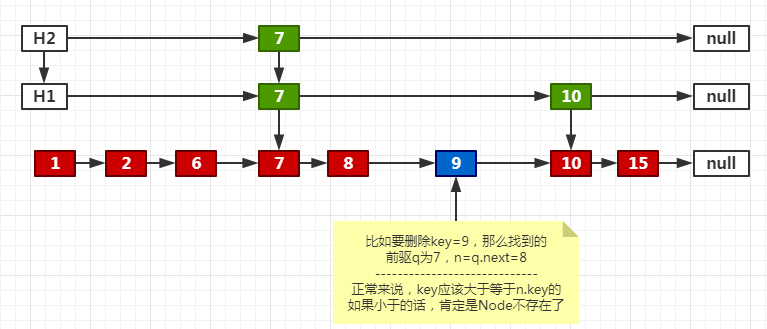
final V doRemove(Object key, Object value) { if (key == null) throw new NullPointerException(); Comparator<? super K> cmp = comparator; // 又是双循环+CAS outer: for (;;) { // 根据key找到前驱b,b的后继n。在这里n是每次与key比较的对象。(b可以理解为before,n可以理解为next) for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) { Object v; int c; // 根据查找位置,我们要删除的key肯定在b的后面某个位置。而此时b的后继是null,那肯定不用删除了,直接跳出双循环。 if (n == null) break outer; // n的后继 Node<K,V> f = n.next; // 数据发生了变化,break,重新循环 if (n != b.next) // inconsistent read break; // n正在删除,帮助删除 if ((v = n.value) == null) { // n is deleted n.helpDelete(b, f); break; } // 前驱b被删除了,break,重新循环 if (b.value == null || v == n) // b is deleted break; // 正常的情况应该大于等于0;如果key小于n.key的话,肯定是个异常情况。 if ((c = cpr(cmp, key, n.key)) < 0) break outer; // 如果key大于n.key,向后移动 if (c > 0) { // 前驱指向当前的n b = n; // 当前的n指向自己的后继 n = f; continue; } // value不为空,代表用户调用的方法是remove(Object key, Object value) // 到了这一步,key是等于n.key的;如果此时value不等于n.value,那就不删除,因为不匹配 if (value != null && !value.equals(v)) break outer; // 删除正式开始:把匹配节点的value置空 if (!n.casValue(v, null)) break; // n.appendMarker(f):给当前节点添加一个删除标记 // b.casNext(n, f):设置前驱b的后继为n的后继 // 如果两个操作有一个没有成功,就执行findNode,清理要删除的节点 if (!n.appendMarker(f) || !b.casNext(n, f)) findNode(key); // retry via findNode else { // 前面操作都成功了,检查这一层的索引是不是为空了,是的话就清理掉 findPredecessor(key, cmp); // clean index if (head.right == null) tryReduceLevel(); } @SuppressWarnings("unchecked") V vv = (V)v; return vv; } } return null; }
对于比较key和n.key的时候
最后看get
private V doGet(Object key) { if (key == null) throw new NullPointerException(); Comparator<? super K> cmp = comparator; // 双循环+CAS outer: for (;;) { // 找到前驱q和前驱的后继n for (Node<K,V> b = findPredecessor(key, cmp), n = b.next;;) { Object v; int c; // 后继无人,无需再找 if (n == null) break outer; // 临时存储后继n的后继 Node<K,V> f = n.next; // 数据变化了,重新循环 if (n != b.next) // inconsistent read break; // n正在被删除,帮助删除 if ((v = n.value) == null) { // n is deleted n.helpDelete(b, f); break; } // 已经删除,返回null if (b.value == null || v == n) // b is deleted break; // 找到了,返回value if ((c = cpr(cmp, key, n.key)) == 0) { @SuppressWarnings("unchecked") V vv = (V)v; return vv; } // 异常情况 if (c < 0) break outer; // 向链表后移动一位 b = n; n = f; } } return null; }
TreeMap
介绍
一个基于红黑树实现的Map,其中的键值对按照自然顺序排序。其中containsKey、get、put和remove操作的时间开销是log(n)。