关于特征筛选中的IV值

1 IV的用途

IV的全称是Information Value，中文意思是信息价值，或者信息量。

我们在用逻辑回归、决策树等模型方法构建分类模型时，经常需要对自变量进行筛选。比如我们有200个候选自变量，通常情况下，不会直接把200个变量直接放到模型中去进行拟合训练，而是会用一些方法，从这200个自变量中挑选一些出来，放进模型，形成入模变量列表。那么我们怎么去挑选入模变量呢？

挑选入模变量过程是个比较复杂的过程，需要考虑的因素很多，比如：变量的预测能力，变量之间的相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），变量在业务上的可解释性（被挑战时可以解释的通）等等。但是，其中最主要和最直接的衡量标准是变量的预测能力。

“变量的预测能力”这个说法很笼统，很主观，非量化，在筛选变量的时候我们总不能说：“我觉得这个变量预测能力很强，所以他要进入模型”吧？我们需要一些具体的量化指标来衡量每自变量的预测能力，并根据这些量化指标的大小，来确定哪些变量进入模型。IV就是这样一种指标，他可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。

2 对IV的直观理解

从直观逻辑上大体可以这样理解“用IV去衡量变量预测能力”这件事情：我们假设在一个分类问题中，目标变量的类别有两类：Y1，Y2。对于一个待预测的个体A，要判断A属于Y1还是Y2，我们是需要一定的信息的，假设这个信息总量是I，而这些所需要的信息，就蕴含在所有的自变量C1，C2，C3，……，Cn中，那么，对于其中的一个变量Ci来说，其蕴含的信息越多，那么它对于判断A属于Y1还是Y2的贡献就越大，Ci的信息价值就越大，Ci的IV就越大，它就越应该进入到入模变量列表中。

3 IV的计算

前面我们从感性角度和逻辑层面对IV进行了解释和描述，那么回到数学层面，对于一个待评估变量，他的IV值究竟如何计算呢？为了介绍IV的计算方法，我们首先需要认识和理解另一个概念——WOE，因为IV的计算是以WOE为基础的。

3.1 WOE

WOE的全称是“Weight of Evidence”，即证据权重。WOE是对原始自变量的一种编码形式。

要对一个变量进行WOE编码，需要首先把这个变量进行分组处理（也叫离散化、分箱等等，说的都是一个意思）。分组后，对于第i组，WOE的计算公式如下：

WOE (weight of Evidence) 字面意思证据权重，对分箱后的每组进行计算。假设 good 为好客户（未 违约），bad 为坏客户（违约）。

                                                                

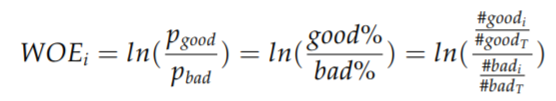
#goodi 表示每组中标签为 good 的数量，#goodT 为 good 的总数量，bad 同理。

3.2 IV

IV (information value) 衡量的是某一个变量的信息量，公式如下：

                                                                 

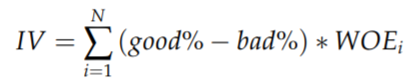
N 为分组的组数，IV 可用来表示一个变量的预测能力。

IV	预测能力
<0.03	无预测能力
0.03-0.09	低
0.1-0.29	中
0.3-0.49	高
>=0.5	极高且可疑

可根据 IV 值来调整分箱结构并重新计算 WOE 和 IV。但并不完全是 IV 值越大越好，还需要考虑 分组数量合适，并且当 IV 值大于 0.5 时，我们需要对这个特征打个疑问，因为它过于太好而显得不够 真实。通常我们会选择 IV 值在 0.1~0.5 这个范围的特征。多数时候分箱都需要手动做一些调整。

python代码如下：

import numpy as np
import pandas as pd
import scipy
import scipy.stats as st

def auto_bin(DF, X, Y, n=5, iv=True, detail=False,q=20):
    """
    自动最优分箱函数，基于卡方检验的分箱

    参数：
    DF: DataFrame 数据框
    X: 需要分箱的列名
    Y: 分箱数据对应的标签 Y 列名
    n: 保留分箱个数
    iv: 是否输出执行过程中的 IV 值
    detail: 是否输出合并的细节信息
    q: 初始分箱的个数

    区间为前开后闭 (]

    返回值：

    """


    # DF = model_data
    # X = "age"
    # Y = "SeriousDlqin2yrs"

    DF = DF[[X,Y]].copy()

    # 按照等频对需要分箱的列进行分箱
    DF["qcut"],bins = pd.qcut(DF[X], retbins=True, q=q, duplicates="drop")
    # 统计每个分段 0，1的数量
    coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut")[Y].count()
    coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut")[Y].count()
    # num_bins值分别为每个区间的上界，下界，0的频次，1的频次
    num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]

    # 定义计算 woe 的函数
    def get_woe(num_bins):
        # 通过 num_bins 数据计算 woe
        columns = ["min","max","count_0","count_1"]
        df = pd.DataFrame(num_bins,columns=columns)

        df["total"] = df.count_0 + df.count_1
        df["percentage"] = df.total / df.total.sum()
        df["bad_rate"] = df.count_1 / df.total
        df["woe"] = np.log((df.count_0/df.count_0.sum()) /
                           (df.count_1/df.count_1.sum()))
        return df

    # 创建计算 IV 值函数
    def get_iv(bins_df):
        rate = ((bins_df.count_0/bins_df.count_0.sum()) -
                (bins_df.count_1/bins_df.count_1.sum()))
        IV = np.sum(rate * bins_df.woe)
        return IV


    # 确保每个分组的数据都包含有 0 和 1
    for i in range(20): # 初始分组不会超过20
        # 如果是第一个组没有 0 或 1，向后合并
        if 0 in num_bins[0][2:]:
            num_bins[0:2] = [(
                num_bins[0][0],
                num_bins[1][1],
                num_bins[0][2]+num_bins[1][2],
                num_bins[0][3]+num_bins[1][3])]
            continue

        # 其他组出现没有 0 或 1，向前合并
        for i in range(len(num_bins)):
            if 0 in num_bins[i][2:]:
                num_bins[i-1:i+1] = [(
                    num_bins[i-1][0],
                    num_bins[i][1],
                    num_bins[i-1][2]+num_bins[i][2],
                    num_bins[i-1][3]+num_bins[i][3])]
                break
        # 循环结束都没有出现则提前结束外圈循环
        else:
            break

    # 重复执行循环至分箱保留 n 组：
    while len(num_bins) > n:
        # 获取 num_bins 两两之间的卡方检验的置信度（或卡方值）
        pvs = []
        for i in range(len(num_bins)-1):
            x1 = num_bins[i][2:]
            x2 = num_bins[i+1][2:]
            # 0 返回 chi2 值，1 返回 p 值。
            pv = st.chi2_contingency([x1,x2])[1]
            # chi2 = scipy.stats.chi2_contingency([x1,x2])[0]
            pvs.append(pv)

        # 通过 p 值进行处理。合并 p 值最大的两组
        i = pvs.index(max(pvs))
        num_bins[i:i+2] = [(
            num_bins[i][0],
            num_bins[i+1][1],
            num_bins[i][2]+num_bins[i+1][2],
            num_bins[i][3]+num_bins[i+1][3])]

        # 打印合并后的分箱信息
        bins_df = get_woe(num_bins)
        if iv:
            print(f"{X} 分{len(num_bins):2}组 IV 值: ",get_iv(bins_df))
        if detail:
            print(bins_df)
    # print("
".join(map(lambda x:f"{x:.16f}",pvs)))
    # 返回分组后的信息
    return get_woe(num_bins) #, get_iv(bins_df)