机器学习数学基础1

线性代数

矩阵

矩阵的定义

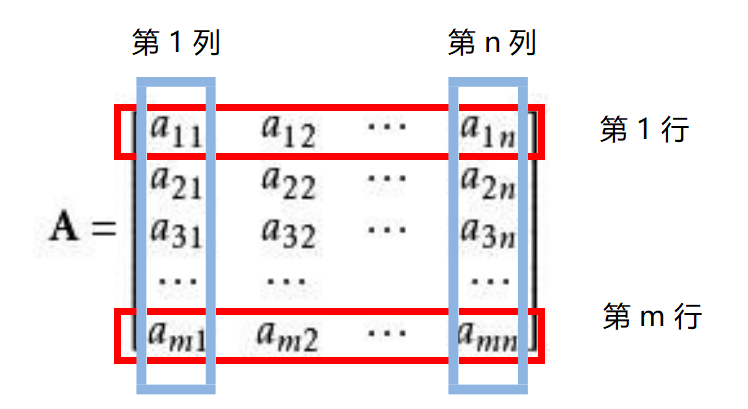
• 由 m × n 个数 aij (i = 1,2,...,m; j = 1,2,...,n) 排成的 m 行 n 列的数表 A 就称为 m 行 n 列的矩阵

• 这 m × n 个数称作矩阵 A 的元素，元素 aij 位于矩阵A 的第i 行第j 列
• m × n 矩阵 A 可以记作 A_m×_n，其中 m是行数，n是列数，m, n > 0

特殊矩阵

对于A_m×_n，如果 m = n，即矩阵的行数与列数相等，那么称A为方阵

矩阵中的概念

• 行数与列数都等于 n 的矩阵称为 n 阶矩阵，又称做 n 阶方阵，可以记作 A_n
• 只有一行的矩阵 A₁×_n 称为行矩阵，又叫行向量
• 同样，只有一列的矩阵 A_n×₁ 称为列矩阵，又叫列向量

 

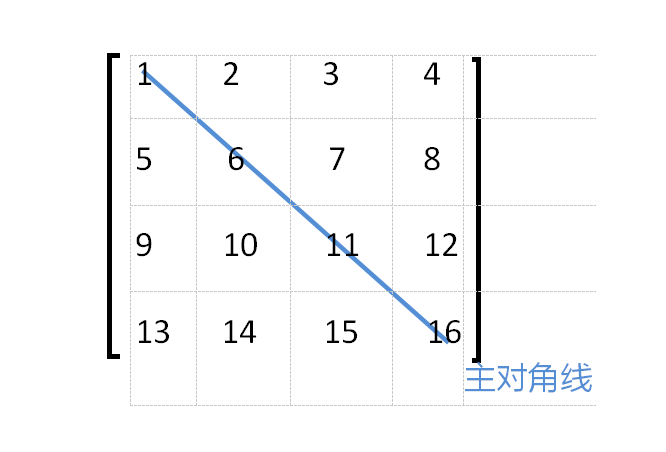
• 对于方阵，从左上角到右下角的直线，叫做主对角线，主对角线上的元素称为主对角

线元素

特殊矩阵

矩阵的元素全部为0，称为零矩阵，用 O 表示

对于方阵，如果只有对角线元素为1，其余元素都为0，

那么称为单位矩阵，一般用 I 或者 E 表示

对于方阵，不在对角线上的元素都为0，

称为对角矩阵

矩阵的加法

• 把矩阵的对应位元素相加
• 矩阵的形状必须一致，即必须是同型矩阵

矩阵的乘法

1. 数与矩阵相乘

数值与矩阵的每一个元素相乘

2.矩阵与矩阵相乘

左矩阵的每一行与右矩阵的每一行，对应每一行元素相乘

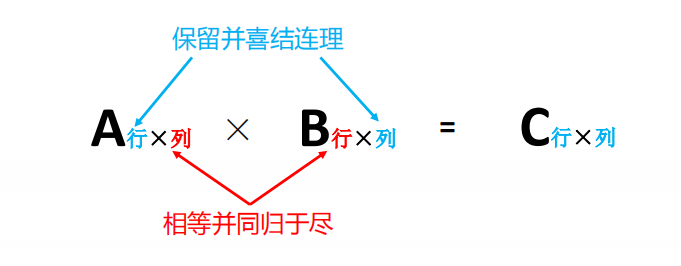
A × B，那么有 A 矩阵 m × n，B 矩阵 n × k，要求左侧矩阵的列数n，必须等于右侧矩阵的行数 n，

必须等于右侧矩阵的行数 n，结果矩阵 C 为 m × k 矩阵。

 

 

 规则：一行乘一列，行定列移动，列尽下一行

 如：

矩阵的转置

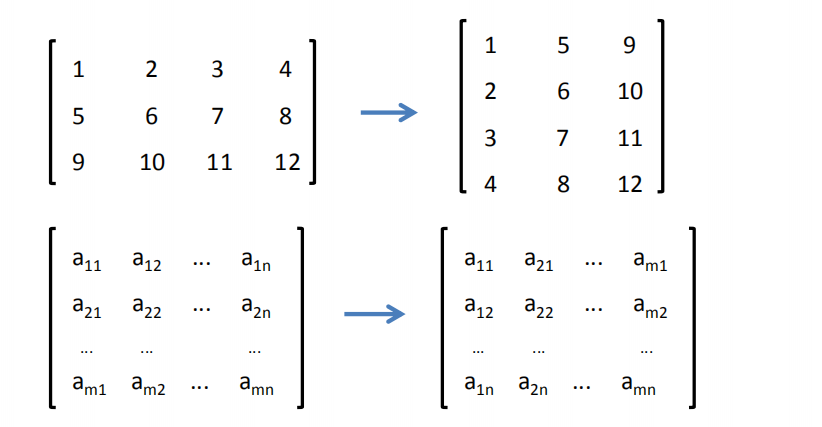
• 把矩阵 A 的行换成相同序数的列，得到一个新矩阵，叫做 A 的转置矩阵，记作 AT
• 行变列，列变行
• A 为 m × n 矩阵，转置之后为 n × m 矩阵

矩阵的运算法则

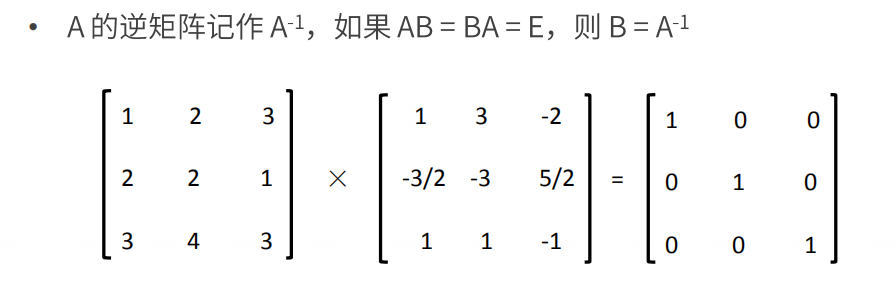
矩阵的逆

——对于 n 阶方阵 A，如果有一个 n 阶方阵 B，使得

　　　　　　AB = BA = E

就称矩阵 A 是可逆的，并把 B 称为 A 的逆矩阵

微积分基本知识

 

 

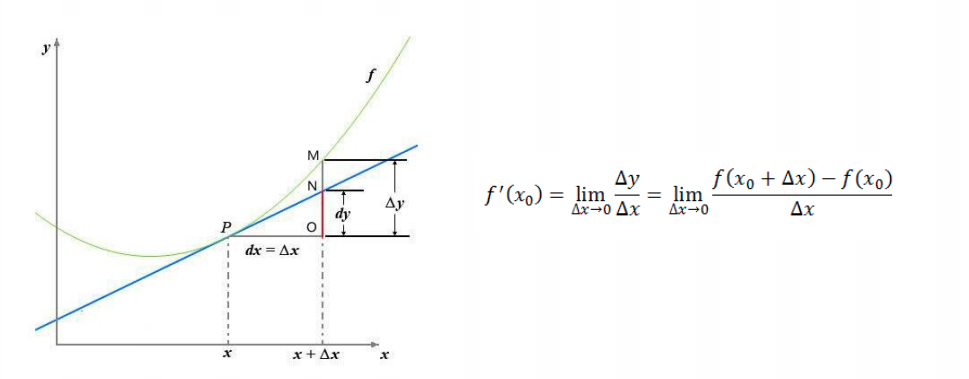
导数

偏导数

方向导数

梯度（Gradient）

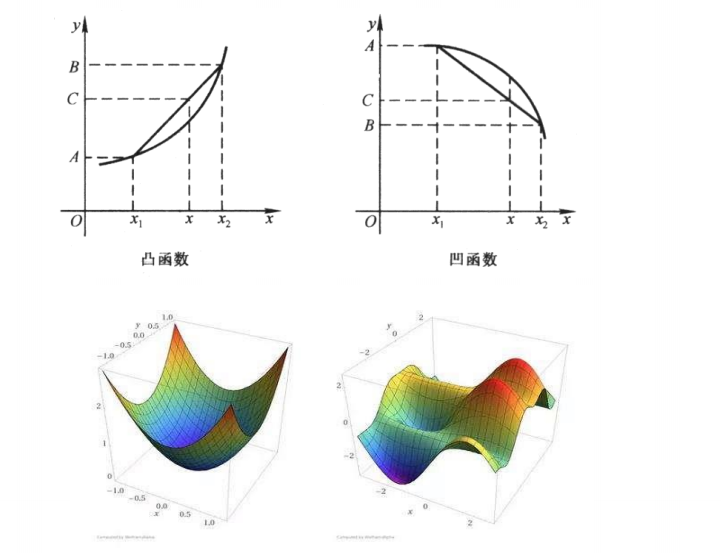
凸函数和凹函数

概率统计基础知识

 

 

常用统计变量

• 样本均值

 

• 样本方差

 

 

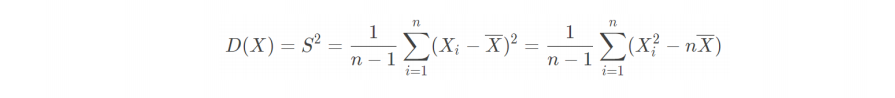
• 样本标准差

 

常见概率分布

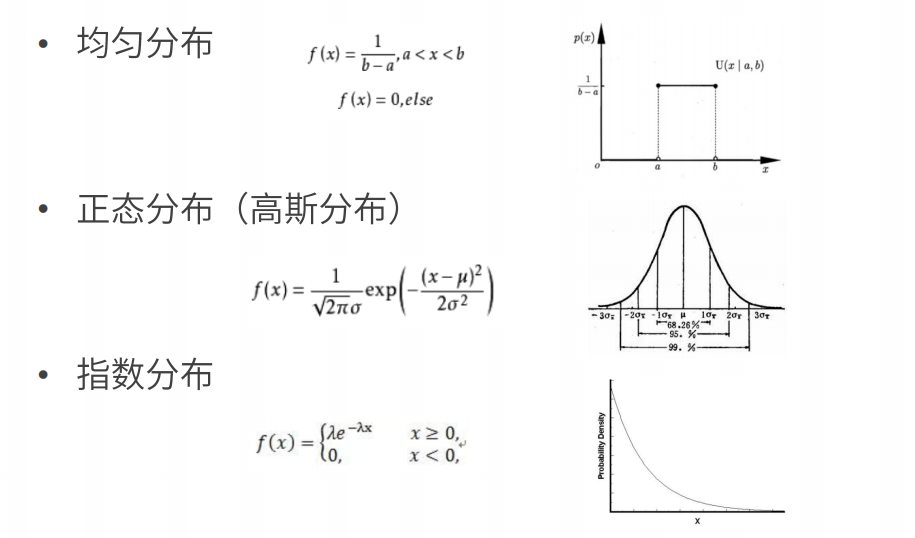
重要概率公式