决策树
-决策树是一种简单高效并且具有强解释性的模型,广泛应用于数据分析领域。
其本质是一颗自上而下的由多个判断节点组成的树
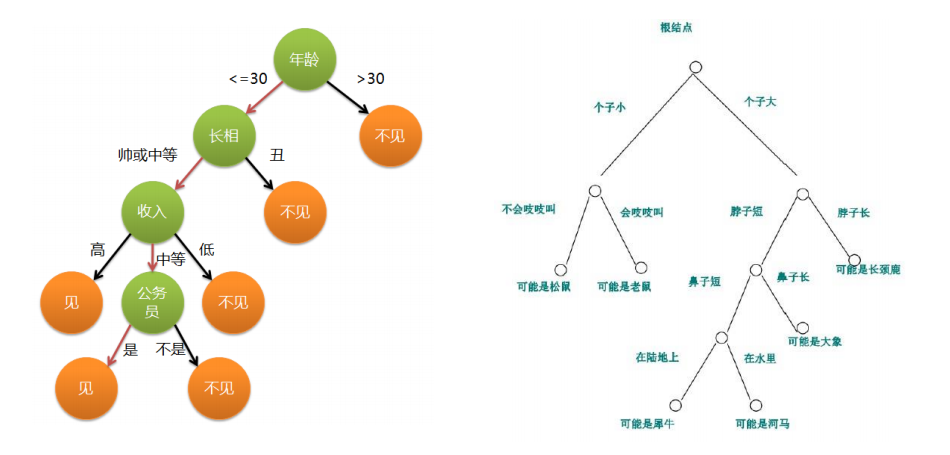
决策树示例
-预测小明今天是否会出门打球


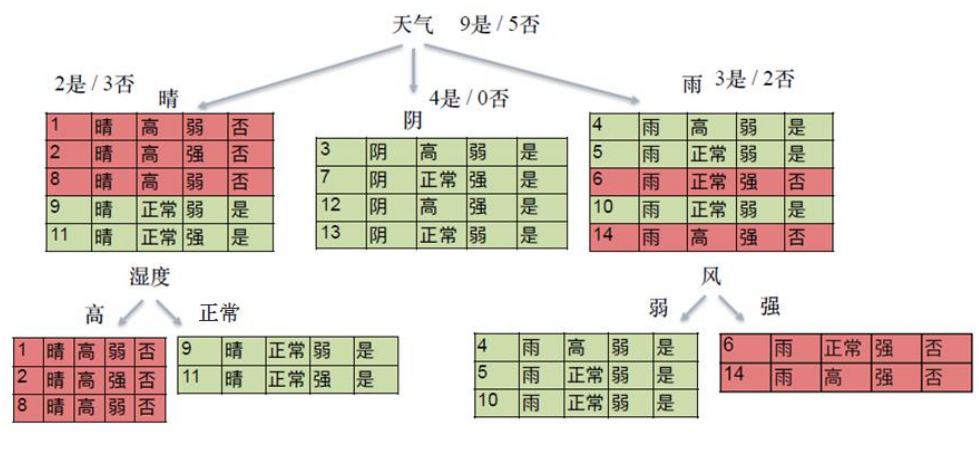
决策树与 if-then 规则
• 决策树可以看作一个if-then规则的集合
• 由决策树的根节点到叶节点的每一条路径,构建一条规则:
路径上内部节点 的特征对应着规则的条件(condition),叶节点对应规则的结论
• 决策树的if-then规则集合有一^重要性质:互斥并且完备。这就是说,
每个实例都被一条规则(一条路径)所覆盖,并且只被这一条规则覆盖

决策树的目标
- 决策树学习的本质,是从训练数据集中归纳出一组if-then分类规则
- 与训练集不相矛盾的决策树,可能有很多个,也可能一个也没有;所以我们 需要选择一个与训练数据集矛盾较小的决策树
- 另一角度,我们可以把决策树看成一个条件概率模型,我们的目标是将实例 分配到条件概率更大的那一类中去
- 从所有可能的情况中选择最优决策树,是一个NP完全问题,所以我们通常采 用启发式算法求解决策树,得到一个次最优解
- 采用的算法通常是递归地进行以下过程:选择最优特征,并根据该特征对训 练数据进行分割,使得各个子数据集都有一个最好的分类
特征选择
- 特征选择就是决定用哪个特征来划分特征空间
随机变量
• 随机变量(random variable)的本质是一个函数,是从样本空间的子集到实 数的映射,将事件转换成一个数值

• 根据样本空间中的元素不同(即不同的实验结果),随机变量的值也将随机产生。 可以说,随机变量是“数值化”的实验结果
• 在现实生活中,实验结果是描述性的词汇,比如“硬币的正面”、“反面”。 在数学家眼里,这些文字化的叙述太过繁琐,所以拿数字来代表它们
熵
• 熵(entropy)用来衡量随机变量的不确定性
• 变量的不确定性越大,炳也就越大 设X是一个取有限个值的离散随机变量,
其概率分布为:
![]()
则随机变量X的炳定义为:
![]()
通常,上式中的对数以2为底或者以e为底(自然对数) ,称为比特(bit)或纳特(nat) 。
当随机变量只取两个值,例如1,0时,则X的分布为:
![]()
熵为:
![]()
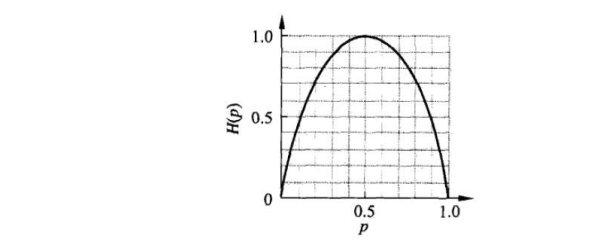
这时,熵H(p)随概率p变化的曲线如下图所示(单位为比特):
- 给三个球分类
显然一眼就可以看出把红球独自一组,黑球一组;
那么从熵的观点来看,是什么情况呢?
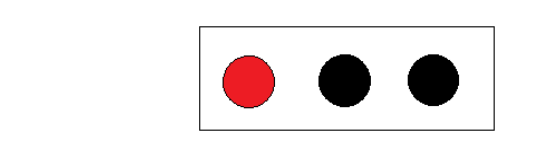
初始状态的熵:
![]()
- 第一种分类方法是一个红球、一个黑球一组,另一个黑球自己一组。
在红黑一组中有红球和黑球,红黑球各自出现的概率是1/2.
在另一组100%出现黑球,红球的概率是0
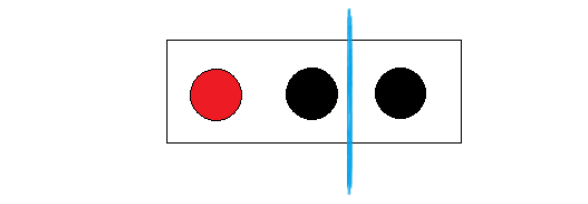

• 第二种分法就是红球自己一组,剩下两个黑球一组
- 在红球组中出现黑球的概率是0,在黑球组中出现红球的概率是0,这样的
分类已经“纯” 了,也就是分类后子集中的随机变量已经变成确定性的了

![]()
决策树的目标
- 我们使用决策树模型的最终目的是利用决策树模型进行分类预测,预测我们 给出的一组数据最终属于哪一种类别,
这是一个由不确定到确定的过程
- 最终理想的分类是,每一组数据,都能确定性地按照决策树分支找到对应的 类别
- 所以我们就选择使数据信息炳下降最快的特征作为分类节点,使得决策树尽快地趋于确定
条件熵(conditional entropy )
- 条件熵 H(Y|X) 表示在已知随机变量X的条件下随机变量Y的不确定性:

- 熵 H(D) 表示对数据集 D 进行分类的不确定性。
- 条件熵 H(D|A) 指在给定特征 A 的条件下数据集分类的不确定性
-当炳和条件炳的概率由数据估计得到时,所对应的炳与条件炳分别称为
经验熵 (empirical entropy) 和经验条件炳 (empirical conditional entropy)
-特征A对训练数据集D的信息增益g(D, A),定义为集合D的经验炳H(D)与特征
A给定条件下D的条件炳H(D|A)之差,即
![]()
-决策树学习应用信息增益准则选择特征
- 经验嫡H(D)表示对数据集D进行分类的不确定性。而经验条件嫡H(D|A)表示在特征A给
定的条件下对数据集D进行分类的不确定性。那么它们的差,即信息增益,
就表示由于 特征A而使得对数据集D的分类的不确定性减少的程度
- 对于数据集D而言,信息增益依赖于特征,不同的特征往往具有不同的信息增益
- 信息增益大的特征具有更强的分类能力
决策树的生成算法
• ID3
- 决策树(ID3)的训练过程就是找到信息增益最大的特征,然后按照此特征进行分类,
然后再找到各类型子集中信息增益最大的特征,然后按照此特征进行分类, 最终得到符合要求的模型。
• C4.5
- C4.5算法在ID3基础上做了改进,用信息增益比来选择特征
• 分类与回归树(CART)
- 由特征选择、树的生成和剪枝三部分组成,既可以用于分类也可以用于回归