JZOJ 4769. 【GDOI2017模拟9.9】graph
题目
Description
对于一个图, 如果它的点集能被分成两个部分, 使得在原图中每一部分之间的点没有任何边相连,则该图被称为二分图。
现在给定一个无向图,每次增加一条边,或者删除一条边。要求您每次判断它是不是二分图。
Input
第一行两个数
n
n
n,
m
m
m,表示该图的点数和操作数。
接下来
m
m
m行,以一个数
t
y
p
e
type
type开头。
t
y
p
e
type
type为
0
0
0或
1
1
1。若
t
y
p
e
type
type为
1
1
1则表示加一条边,接下来输入两个数
a
a
a,
b
b
b表示它连接的边的编号,编号从
0
0
0到
n
−
1
n-1
n−1;为
0
0
0则表示删除一条边,接下来是一个数
a
a
a表示删除加入的第
a
+
1
a+1
a+1条边。
保证任何时候图都无重边或自环。
Output
m m m行,每行一个"YES"或"NO"(引号不输出),表示每次操作后图是否是二分图。
Sample Input
3 3
1 0 1
1 0 2
1 1 2
Sample Output
YES
YES
NO
Data Constraint
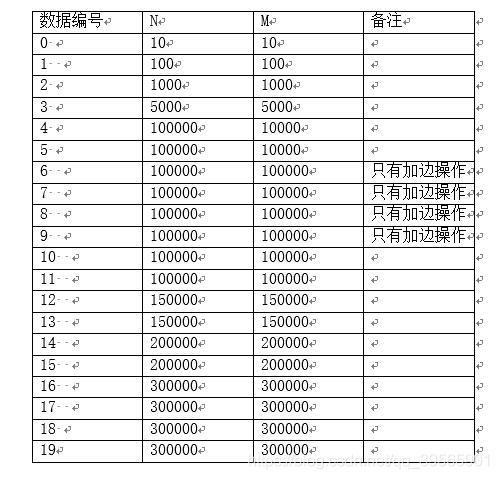
题解
- 首先需要知道怎么判断一个图是否是二分图,
- 这个很简单,题目中也交代了,
- 但执行每次操作(加边)的过程中,怎么更方便地判断呢?
- 显然可以知道,如果一个非二分图,再怎么加边都不可能是二分图,
- 那么对于一个二分图,怎么加边后就不是二分图了呢?
- 分析:
- 对于一棵树来说,肯定是一个二分图,只要保证儿子和父亲不分在同一边就行了,
- 那么非二分图就肯定不是树,则说明有环,同时不难发现,还要是奇环(偶环是二分图)。
- 所以可以用并查集来维护。
- 但!!!
- 还有删除操作!
-
只有加边
- 并查集,按秩合并,维护父亲 f [ x ] f[x] f[x]、到父亲的距离 f s [ x ] fs[x] fs[x]、子树的树高 d [ x ] d[x] d[x],
- 加入一条边,如果两点在同一子树上,判断 f s [ x ] + f s [ y ] fs[x]+fs[y] fs[x]+fs[y]为偶数(加上这条边后就形成奇环),那么就不是二分图;如果两点不在同一子树上,在两个根结点间连上一条长度为 f s [ x ] + f s [ y ] + 1 fs[x]+fs[y]+1 fs[x]+fs[y]+1的边。
-
线段树初阶做法
- 将每条边的出现时间挂在线段数上,如 [ 4 , 33 ] [4,33] [4,33]分为 [ 4 , 4 ] , [ 5 , 8 ] , [ 9 , 16 ] , [ 17 , 32 ] , [ 33 , 33 ] [4,4],[5,8],[9,16],[17,32],[33,33] [4,4],[5,8],[9,16],[17,32],[33,33]对应的存在线段树的各个节点上(这些区间都是线段树节点对应在区间),
- 每次从根结点进入,一直到每个叶子节点,中间把经过了的标记了的边给连上,方法如上。
-
线段树快速做法
- 这样会发现相邻的两个叶子节点从根进入后的路径很多相同,会进行大量重复计算,所以不妨改进。
- 从根节点开始遍历整棵线段树,每进入一个节点,修改 f , f s , d f,fs,d f,fs,d的同时,把原来的值记录下来,回溯后再修改回去,然后继续遍历。
- 递归时如果当前的答案已经为NO了,那么以上操作可以跳过,只用把当前区间的答案都变成NO即可。
代码
#include<cstdio>
#include<cstring>
using namespace std;
#define N 300001
struct
{
int x,y,t;
}a[N];
int len=0,last[N*4],next[20*N],to[20*N];
int h[N*4],f[N],fs[N],dp[N],ls[N*4];
int bz[N],ans=1,ps,qs;
struct
{
int v,x,t,s,d;
}ch[40*N];
void ad(int x,int y)
{
to[++len]=y;
next[len]=last[x];
last[x]=len;
}
void add(int v,int l,int r,int x,int y,int c)
{
if(l==x&&r==y) ad(v,c);
else
{
int mid=(l+r)/2;
if(y<=mid) add(v*2,l,mid,x,y,c);
else if(x>mid) add(v*2+1,mid+1,r,x,y,c);
else add(v*2,l,mid,x,mid,c),add(v*2+1,mid+1,r,mid+1,y,c);
}
}
int get(int k,int &s)
{
if(f[k]==k) return k;
else
{
s+=fs[k];
int p=get(f[k],s);
return p;
}
}
void make(int v,int x)
{
if(ls[x]==v) return;
ls[x]=v;
len++;
if(h[v]==0) h[v]=len;
ch[len].v=v,ch[len].x=x,ch[len].t=f[x],ch[len].s=fs[x],ch[len].d=dp[x];
}
void dfs(int v,int l,int r)
{
int ans1=ans;
if(ans)
{
for(int i=last[v];i;i=next[i])
{
int x=to[i];
ps=qs=0;
int p=get(a[x].x,ps),q=get(a[x].y,qs);
if(p!=q)
{
make(v,p);
make(v,q);
if(dp[p]<dp[q])
{
f[p]=q;
fs[p]=(ps+qs+1)%2;
if(dp[p]+1>dp[q]) dp[q]=dp[p]+1;
}
else
{
f[q]=p;
fs[q]=(ps+qs+1)%2;
if(dp[q]+1>dp[p]) dp[p]=dp[q]+1;
}
}
else if((ps+qs)%2==0) ans=0;
}
}
if(l==r)
{
if(ans) printf("YES
"); else printf("NO
");
}
else
{
int mid=(l+r)/2;
dfs(v*2,l,mid);
dfs(v*2+1,mid+1,r);
}
for(int i=h[v];ch[i].v==v&&i<=len;i++)
{
int x=ch[i].x;
f[x]=ch[i].t,fs[x]=ch[i].s,dp[x]=ch[i].d;
}
ans=ans1;
}
int main()
{
int n,m,i,p,x,ln=0;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d",&p);
if(p==0)
{
scanf("%d",&x);
x++;
add(1,1,m,a[x].t,i-1,x);
bz[x]=0;
}
else
{
bz[++ln]=1;
scanf("%d%d",&a[ln].x,&a[ln].y);
a[ln].x++,a[ln].y++,a[ln].t=i;
}
}
for(i=1;i<=ln;i++) if(bz[i]) add(1,1,m,a[i].t,m,i);
len=0;
for(i=1;i<=n;i++) f[i]=i,fs[i]=0,dp[i]=0;
dfs(1,1,m);
return 0;
}