可以作一个类比:讲角度当成位置,转过的角度当成位移,然后我们命名为角位置和角位移。
然后再类比于普通的运动,描述一个角量化的运动。在这种运动中,有:
位移→角位移θ
速度→角速度ω
加速度→角加速度(即角速度的瞬时变化率)阿尔法
时间→时间
这些是运动学参量,然后再考虑动力学,即牛顿第二定律的几个参量:
质量→转动惯量I(在数值上,为mr²) moment of inertia
力→力矩 t(t=Fr)
故角量表示下的牛顿第二定律就是:t=I阿尔法(有些书称之为转动定理)//F=ma /// 推导:Fr=mar / a=阿尔法 r
要是继续类比,又有:
动量→角动量L(类比p=mv,有L=Iω)
动能→转动动能(½Iω²=½mr²ω²=½mv(切向速度)²)
所以你可以说,角动量就是角量运动中的动量
在某些地方说,在外力矩为零时,角动量守恒,这其实就是我们高中说的:在合外力为零时动量守恒。
不知道这样子讲能不能理解
转载:
可以作一个类比:讲角度当成位置,转过的角度当成位移,然后我们命名为角位置和角位移。
然后再类比于普通的运动,描述一个角量化的运动。在这种运动中,有:
位移→角位移θ
速度→角速度ω
加速度→角加速度(即角速度的瞬时变化率)β
时间→时间
这些是运动学参量,然后再考虑动力学,即牛顿第二定律的几个参量:
质量→转动惯量I(在数值上,为mr²,微分)
力→力矩M(M=Fr)
故角量表示下的牛顿第二定律就是:t=Iβ(有些书称之为转动定理)
要是继续类比,又有:
动量→角动量L(类比p=mv,有L=Iω)
动能→转动动能(½Iω²=½mr²ω²=½mv(切向速度)²)
所以你可以说,角动量就是角量运动中的动量
在某些地方说,在外力矩为零时,角动量守恒,这其实就是我们高中说的:在合外力为零时动量守恒。
不知道这样子讲能不能理解
转载:
https://www.zhihu.com/question/22217331/answer/426852533
栗子:


下面这个要记住:
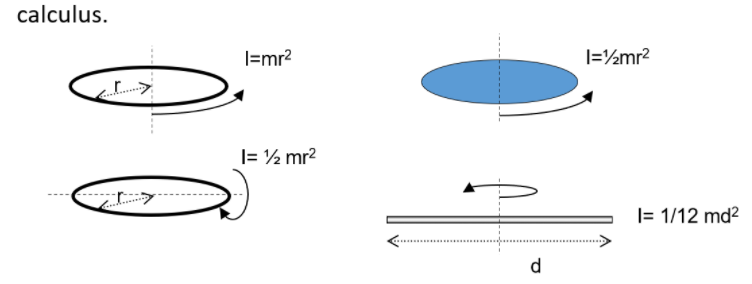
单位:
- I = kg m^2
- α= rad/s^-2
- t= NM
常用的东东:
- a=α R