1、算法简介

　　1.1　更佳的查找方式

　　　　二分查找是一种算法，其输入是一个有序的元素列表。如果要查找的元素包含在列表中，二分查找返回其位置，否则返回null。

　　　　一般而言，对于包含 n 个元素的列表，用二分查找最多需步，而简单查找最多需要 步。

　　　　仅当列表是有序的时候，二分查找才管用。

　　　　代码清单1-1　二分查找

# -*- coding: utf-8 -*-
def binary_search(list1, item):
    # （以下2行）low和high用于跟踪要在其中查找的列表部分
    low = 0
    high = len(list1)-1

    # 只要范围没有缩小到只包含一个元素，
    while low <= high:
        # 就检查中间的元素
        mid = (low + high) / 2
        guess = list1[mid]
        # 找到了元素
        if guess == item:
            return mid
        # 猜的数字大了
        if guess > item:
            high = mid - 1
        # 猜的数字小了
        else:
            low = mid + 1
    # 没有指定的元素
    return None


my_list = [1, 3, 5, 7, 9]
# => 1,别忘了索引从0开始，第二个位置的索引为1
print binary_search(my_list, 3)
# => None,在Python中，None表示空，它意味着没有找到指定的元素
print binary_search(my_list, -1)

　　1.2　运行时间

 　　　　一般而言，应选择效率最高的算法，以最大限度地减少运行时间或占用空间。

　　　　线性时间（linear time）：最多需要猜测的次数与列表长度相同。

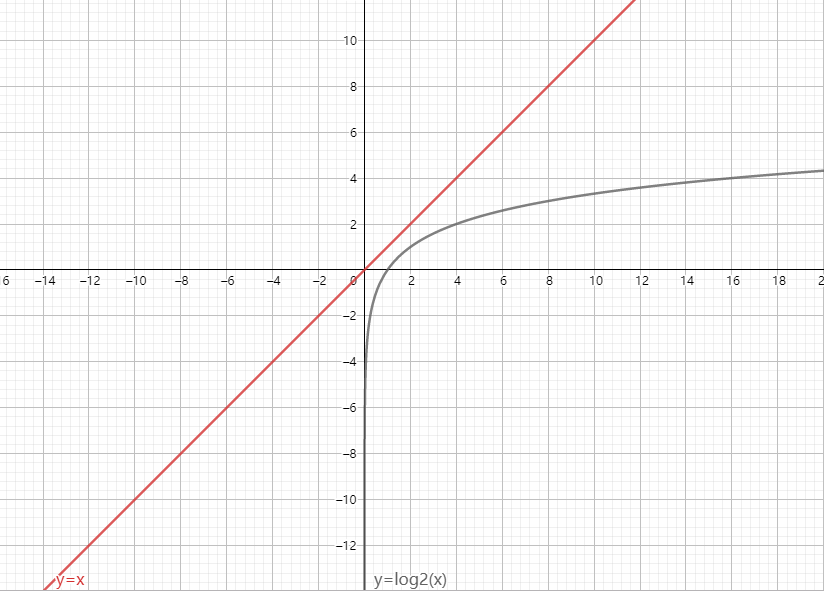
　　　　对数时间（log时间）：二分 查找的时间为对数时间。

　　1.3　大O表示法

　　　　大O表示法是一种特殊的表示法，指出了算法的速度有多快。

　　　　随着元素数量的增加，二分查找需要的额外时间并不多，而简单查找的额外时间却很多。因此，随着列表的增长，二分查找的速度比简单查找快得多。

　　　　

　　　　大O表示法指出了算法有多快。例如，假设列表包含n个元素。简单查找需要检查每个元素，因此需要执行 n 次操作。使用大O表示法，这个运行时间为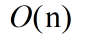。二分查找需要执行，使用大O表示法，这个运行时间为。

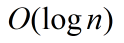　　　　大O表示法让你能比较操作数，它指出了算法运行时间的增速。

　　　　1.4　一些常见的大O运行时间

　　　　，也叫对数时间，这样的算法包括二分查找。

　　　　，也叫线性时间，这样的算法包括简单查找。

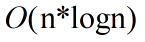　　　　，这样的算法包括快速排序——一种速度较快的排序算法。

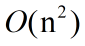　　　　，这样的算法包括选择排序——一种速度较慢的排序算法。

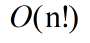　　　　，这样的算法包括旅行商问题的解决方案——一种非常慢的算法。

　　　　1.5　旅行商

　　　　有一位旅行商，他需要前往5个城市。这位旅行商要前往5个城市，同时要确保旅程最短。为此，可考虑前往这些城市的各种可能顺序。对于每种顺序，他都计算总旅程，再挑选出旅程最短的路线。5个城市有5！=5*4*3*2*1=120中不同的排列方式。因此，在涉及5个城市时，解决这个问题需要执行120次操作。

　　　　推而广之，涉及n个城市时，需要执行n!（n的阶乘）次操作才能计算出结果。因此运行时间为，即阶乘时间。