题目大意:n组数据,每组数据有两个数ci和sumi,选取ci个非负数ai,使得$sum ^{c_{i}}_{k=1}a_{k}geq sum_{i}$,且最小化$sum ^{c_{i}}_{k=1}a^{2}_{k}$,求最小值。
由均值不等式可知当每个ak=$dfrac {sum_{i}}{c_{i}}$时有最小的$sum ^{c_{i}}_{k=1}a^{2}_{k}$,但ak需要整数,那我们先对前x个数取ak+1,直到剩下的ci-x个数都取ak时有$sum ^{c_{i}}_{k=1}a_{i}=sum_{i}$,此时$sum ^{c_{i}}_{k=1}a^{2}_{k}$最小。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 template <typename T> 5 void read(T &x) { 6 int s = 0, c = getchar(); 7 x = 0; 8 while (isspace(c)) c = getchar(); 9 if (c == 45) s = 1, c = getchar(); 10 while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); 11 if (s) x = -x; 12 } 13 14 template <typename T> 15 void write(T x, char c = ' ') { 16 int b[40], l = 0; 17 if (x < 0) putchar(45), x = -x; 18 while (x > 0) b[l++] = x % 10, x /= 10; 19 if (!l) putchar(48); 20 while (l) putchar(b[--l] | 48); 21 putchar(c); 22 } 23 24 void Input(void) { 25 int n; 26 read(n); 27 for(int c,sum,i=1;i<=n;++i){ 28 read(c); 29 read(sum); 30 if (sum%c==0){ 31 int ans=sum*sum/c; 32 printf("%d ",ans); 33 } 34 else{ 35 int qwq=sum/c; 36 int cnt=c; 37 int ans=0; 38 while(qwq*cnt<sum){ 39 ans+=(qwq+1)*(qwq+1); 40 --cnt; 41 sum-=qwq+1; 42 } 43 ans+=qwq*qwq*cnt; 44 printf("%d ",ans); 45 } 46 } 47 } 48 49 void Solve(void) {} 50 51 void Output(void) {} 52 53 main(void) { 54 freopen("input.txt", "r", stdin); 55 freopen("output.txt", "w", stdout); 56 Input(); 57 Solve(); 58 Output(); 59 }
B. Obtain Two Zeroes (CF 1260 B)
题目大意:两个数a,b,可以选择任意一个正整数x,令a=a-x,b=b-2*x,或者a=a-2*x,b=b-2*x。经历若干次操作后,问能否使得两个数同时为0.
我们先取x=abs(a-b),选择其中一种操作方式使得a,b值相等,此时如果小于0则不可能使得同时为0,否则判断其是否是3的倍数,是则可以,否则不可。
因为两数相等后,我们要时时保证两数继续相等,很显然我们是要取同一个x进行两次操作,对应的操作方式不相同,这样两个数都分别减去了3*x,如果该数不是3的倍数,则不可能会减到0.

1 #include <bits/stdc++.h> 2 #define MIN(a,b) ((((a)<(b)?(a):(b)))) 3 #define ABS(a) (((a)<0?-(a):(a))) 4 using namespace std; 5 6 template <typename T> 7 void read(T &x) { 8 int s = 0, c = getchar(); 9 x = 0; 10 while (isspace(c)) c = getchar(); 11 if (c == 45) s = 1, c = getchar(); 12 while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); 13 if (s) x = -x; 14 } 15 16 template <typename T> 17 void write(T x, char c = ' ') { 18 int b[40], l = 0; 19 if (x < 0) putchar(45), x = -x; 20 while (x > 0) b[l++] = x % 10, x /= 10; 21 if (!l) putchar(48); 22 while (l) putchar(b[--l] | 48); 23 putchar(c); 24 } 25 26 void Input(void) { 27 int x,y; 28 read(x); 29 read(y); 30 int qwq=MIN(x,y)-ABS(x-y); 31 if (qwq>=0&&qwq%3==0) printf("YES "); 32 else printf("NO "); 33 } 34 35 void Solve(void) {} 36 37 void Output(void) {} 38 39 main(void) { 40 int kase; 41 freopen("input.txt", "r", stdin); 42 freopen("output.txt", "w", stdout); 43 read(kase); 44 for (int i = 1; i <= kase; i++) { 45 //printf("Case #%d: ", i); 46 Input(); 47 Solve(); 48 Output(); 49 } 50 }
题目大意:有10100块板,从0开始编号,T组数据,每组数据给定两个数r,b,若编号能被r整除,则该板被涂为红色,若能被b整除,则该板被涂为蓝色,若编号能同时被r和b整除,则你可以选择该板是涂为红色还是蓝色,其余情况的板不涂色。然后把所有涂了色的板拿出来并按编号升序排列,从左到右,若出现k块连续的颜色相同的板,则要遭受惩罚。问你能否避免该惩罚。
我们假设r<b,我们k*b位置涂蓝色,然后(k+1)*b位置也涂蓝色,现在问题就在于在区间[k*b,(k+1)*b]内是否有k个及以上的r的倍数,由于k不同,在区间[k*b,(k+1)*b]第一个出现r的倍数的位置距离k*b的长度可能不同,最坏情况下就是找到一个k,使得第一个出现r的倍数的位置距离k*b最小,此时在区间[k*b,(k+1)*b]里出现的r的倍数的数是最多的。我们可以遍历k,从0到lcm(r,b)/b,但这显然会超时。
我们知道,对于一个有n个数,编号0到n-1,围成圈排列,每往前数k个数选一个,如5个数,每往前数三个数选一个,则依次选中的编号为:3,1,4,2,0,3,1,4,2,0,......循环无限下去,最终相当于是每往前数1个数选一个
对于n个数,每往前数k个数选一个,可以证明,这相当于是每往前数gcd(n,k)个数选一个,即第一个出现r的倍数的位置距离k*b最小为gcd(r,b),那么原本(k*b,(k+1)*b)区间里有b-1个正整数,除去前gcd(r,b)个,剩下的数的个数除以r即可得到这里面有多少个r的倍数,再加上第一个r的倍数一个,即为区间[k*b,(k+1)*b]内最多有的r的倍数的个数,如果它小于k,就OBEY,否则REBEL。即判断$dfrac {b-1-gcd left( r,b ight) }{r}+1$与k的关系

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 template <typename T> 5 void read(T &x) { 6 int s = 0, c = getchar(); 7 x = 0; 8 while (isspace(c)) c = getchar(); 9 if (c == 45) s = 1, c = getchar(); 10 while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); 11 if (s) x = -x; 12 } 13 14 template <typename T> 15 void write(T x, char c = ' ') { 16 int b[40], l = 0; 17 if (x < 0) putchar(45), x = -x; 18 while (x > 0) b[l++] = x % 10, x /= 10; 19 if (!l) putchar(48); 20 while (l) putchar(b[--l] | 48); 21 putchar(c); 22 } 23 24 long long gcd(long long a,long long b){ 25 if (a==0) return b; 26 else return gcd(b%a,a); 27 } 28 void Input(void) { 29 long long r,b,k; 30 read(r); 31 read(b); 32 read(k); 33 if (r>b){ 34 r=r^b; 35 b=r^b; 36 r=r^b; 37 } 38 long long qwq=gcd(r,b); 39 if ((b-1-qwq)/r+1<k) printf("OBEY "); 40 else printf("REBEL "); 41 } 42 43 void Solve(void) {} 44 45 void Output(void) {} 46 47 main(void) { 48 int kase; 49 freopen("input.txt", "r", stdin); 50 freopen("output.txt", "w", stdout); 51 read(kase); 52 for (int i = 1; i <= kase; i++) { 53 //printf("Case #%d: ", i); 54 Input(); 55 Solve(); 56 Output(); 57 } 58 }
D. A Game with Traps (CF 1260 D)
题目大意:m个士兵,每个士兵有一个敏捷值ai,在一个数轴上,0到n+1,你要带士兵从0位置到n+1的位置,现在数轴上有k个陷阱,第i个陷阱位置在li,它有个危险值di,如果士兵的敏捷值ai小于该陷阱的危险值di,则该士兵会被干掉,但很幸运,对于每个陷阱i,如果你去到位置ri,你即可解除第i个陷阱的危险。现在你需要带一定数量的士兵从0到n+1,你免疫陷阱,但士兵不免疫,在规定的时间T内,你需要把全部你选择的士兵带到n+1处,你单独或者带着士兵从x移动到x+1或x-1需要消耗时间1,解除陷阱不需要时间。求你最大可以带的士兵数量。
首先从0移动到n+1至少消耗n+1的时间,为了解除陷阱需要额外的移动从而有额外的时间,并且我们发现我们选的士兵的敏捷值的最小值决定了我们要解除的陷阱是哪些,对于敏捷值最小值为x的情况能够成功在规定时间到达n+1,那么在最小值y>x的情况下也能满足,于是我们先对士兵的敏捷值进行从大到小排序,然后二分敏捷值的最小值,判断能否在规定的时间到达n+1。在判断中,当我们解除了某个陷阱时,我们有两个选择,继续向前走解除下一个陷阱,或者回去带士兵前进,通过画图我们可以发现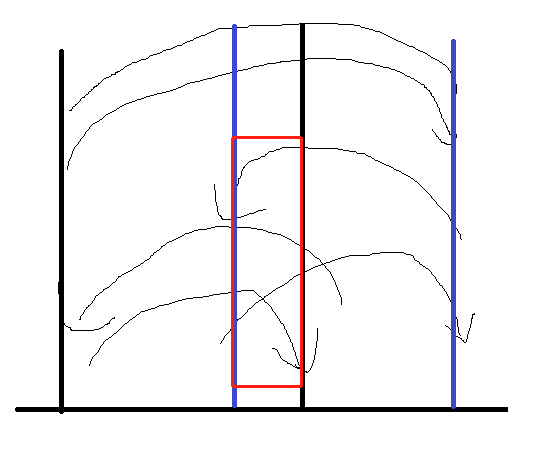
不同颜色即为不同陷阱,这种情况下显然我们一次性解除这两个陷阱是更优的,因为如果分两次解决的话,打框框的部分就会被重复走,浪费时间。即我们把每个陷阱抽象成左括号,解除陷阱的位置抽象成右括号,通过括号匹配,合并有交集的括号,这样子对于一整个区间的陷阱我们一并解除,这种决策是最优的。时间复杂度O(klogm)

1 #include <bits/stdc++.h> 2 #define MAX(a,b) ((((a)>(b)?(a):(b)))) 3 using namespace std; 4 5 template <typename T> 6 void read(T &x) { 7 int s = 0, c = getchar(); 8 x = 0; 9 while (isspace(c)) c = getchar(); 10 if (c == 45) s = 1, c = getchar(); 11 while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); 12 if (s) x = -x; 13 } 14 15 template <typename T> 16 void write(T x, char c = ' ') { 17 int b[40], l = 0; 18 if (x < 0) putchar(45), x = -x; 19 while (x > 0) b[l++] = x % 10, x /= 10; 20 if (!l) putchar(48); 21 while (l) putchar(b[--l] | 48); 22 putchar(c); 23 } 24 25 const int N=2e5+5; 26 27 int n,m,k,t; 28 29 int a[N]; 30 31 struct data{ 32 int l,r,d; 33 }trap[N]; 34 35 bool cmp(const struct data &a,const struct data &b){ 36 if (a.l<b.l) return true; 37 if (a.l>b.l) return false; 38 if (a.r<b.r) return true; 39 if (a.r>b.r) return false; 40 if (a.d<b.d) return true; 41 return false; 42 } 43 44 bool cmp1(int a,int b){ 45 return a>b; 46 } 47 void Input(void) { 48 read(m); 49 read(n); 50 read(k); 51 read(t); 52 t-=n+1; 53 for(int i=1;i<=m;++i) read(a[i]); 54 for(int i=1;i<=k;++i){ 55 read(trap[i].l); 56 read(trap[i].r); 57 read(trap[i].d); 58 } 59 sort(trap+1,trap+1+k,cmp); 60 sort(a+1,a+1+m,cmp1); 61 } 62 63 bool check(int x){ 64 int qwq=t; 65 int le=1,max_r=0; 66 for(int tmp=0,i=1;i<=k+1;++i){ 67 if (trap[i].d<=a[x]) continue; 68 if (tmp==0){ 69 le=trap[i].l-1; 70 max_r=trap[i].r; 71 tmp=1; 72 continue; 73 } 74 if (max_r<trap[i].l){ 75 qwq-=(max_r-le)*2; 76 le=trap[i].l-1; 77 } 78 max_r=MAX(max_r,trap[i].r); 79 if (qwq<0) return false; 80 } 81 //printf("%d %d ",x,qwq); 82 return true; 83 } 84 85 void Solve(void) { 86 int ans=0; 87 int l=1,r=m+1; 88 trap[k+1].l=n+5; 89 trap[k+1].r=n+9; 90 trap[k+1].d=2e5+8; 91 while(l<r){ 92 int mid=(l+r)>>1; 93 if (check(mid)) ans=mid,l=mid+1; 94 else r=mid; 95 } 96 write(ans,' '); 97 } 98 99 void Output(void) {} 100 101 main(void) { 102 freopen("input.txt", "r", stdin); 103 freopen("output.txt", "w", stdout); 104 Input(); 105 Solve(); 106 Output(); 107 }
