A. Even But Not Even (CF 1291 A)
题目大意
给定一个数,要求删去其中的一些数字后所得的数是奇数但各位数的和为偶数。
解题思路
保留两位奇数即可,其中一个奇数在末位。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int kase; read(kase);
for (int i = 1; i <= kase; i++) {
int n;
char s[3006]={0};
read(n);
scanf("%s",s);
int fir=-1,sec=-1;
for(int i=0;i<n;++i)
if ((s[i]-'0')&1)
if (fir==-1) fir=i;
else if (sec==-1) sec=i;
else break;
if (sec==-1) puts("-1");
else s[sec+1]=0,printf("%s
",s);
}
return 0;
}
B. Array Sharpening (CF 1291 B)
题目大意
给定一个有(n)个数的数字序列(a),可以对序列里的任意正数多次减一,要求将序列变成先严格递增后严格递减,也可以单增或单减,问能否做到。
解题思路
我们让波峰尽可能靠右,波峰左边的就看它是否(a[i]geq i)((i)从(0)开始),第一个不满足该不等式的位置当做波峰,波峰的右边包括波峰看其是否满足(a[i]geq n-i-1(i>k)),都满足则可,否则不可。因为我们让波峰尽可能靠右,这样对于波峰右边的数所需要满足的条件就不会那么苛刻。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
bool solve(int n,int a[]){
int qwq=0;
while(qwq<n&&a[qwq]>=qwq) ++qwq;
if (qwq==n) return true;
--qwq;
while(qwq<n&&a[qwq]>=n-qwq-1) ++qwq;
if (qwq==n) return true;
return false;
}
int main(void) {
int kase; read(kase);
for (int i = 1; i <= kase; i++) {
int n;
read(n);
int a[n];
for(int i=0;i<n;++i) read(a[i]);
if (solve(n,a)) puts("Yes");
else puts("No");
}
return 0;
}
C. Mind Control (CF 1291 C)
题目大意
给定(n)个数,有(n)个人,你第(m)次拿,对于每个人来说,他们可以拿第一个数或最后一个数,现在在取数开始前,你可以指定最多(k)个人,当他们拿的时候规定他们分别是拿第一个数还是最后一个数。而没有被你指定的人,当他们取的时候,他们有可能拿第一个数也可能拿最后一个数。现在需要你指定最多(k)个人,来使得不管其他人怎么取,到你取的时候,你取到的数始终大于等于(x),且这个(x)尽可能大。
解题思路
前(m-1)个人取后,剩下的是连续的(n-m+1)个数。如果(k=0)的话,那么到我取的时候情况数就有(m)种,而答案就是这(m)种情况中第一个和最后一个数的最大值的最小值。我们考虑如果指定了一个人的话,对最终的情况数会有什么影响。
我们把这个取数过程的状态树画出来,会有(m)层,进而能发现,如果对其中任意一个人进行指定,那么最边边上的状态就会取不到了,最终的情况数就只有(m-1)种,而这(m-1)种就有两种可能。如果指定(k)个人,那么最终的情况数就只有(m-k)种,且这(m-k)种情况在状态树中是连续的。
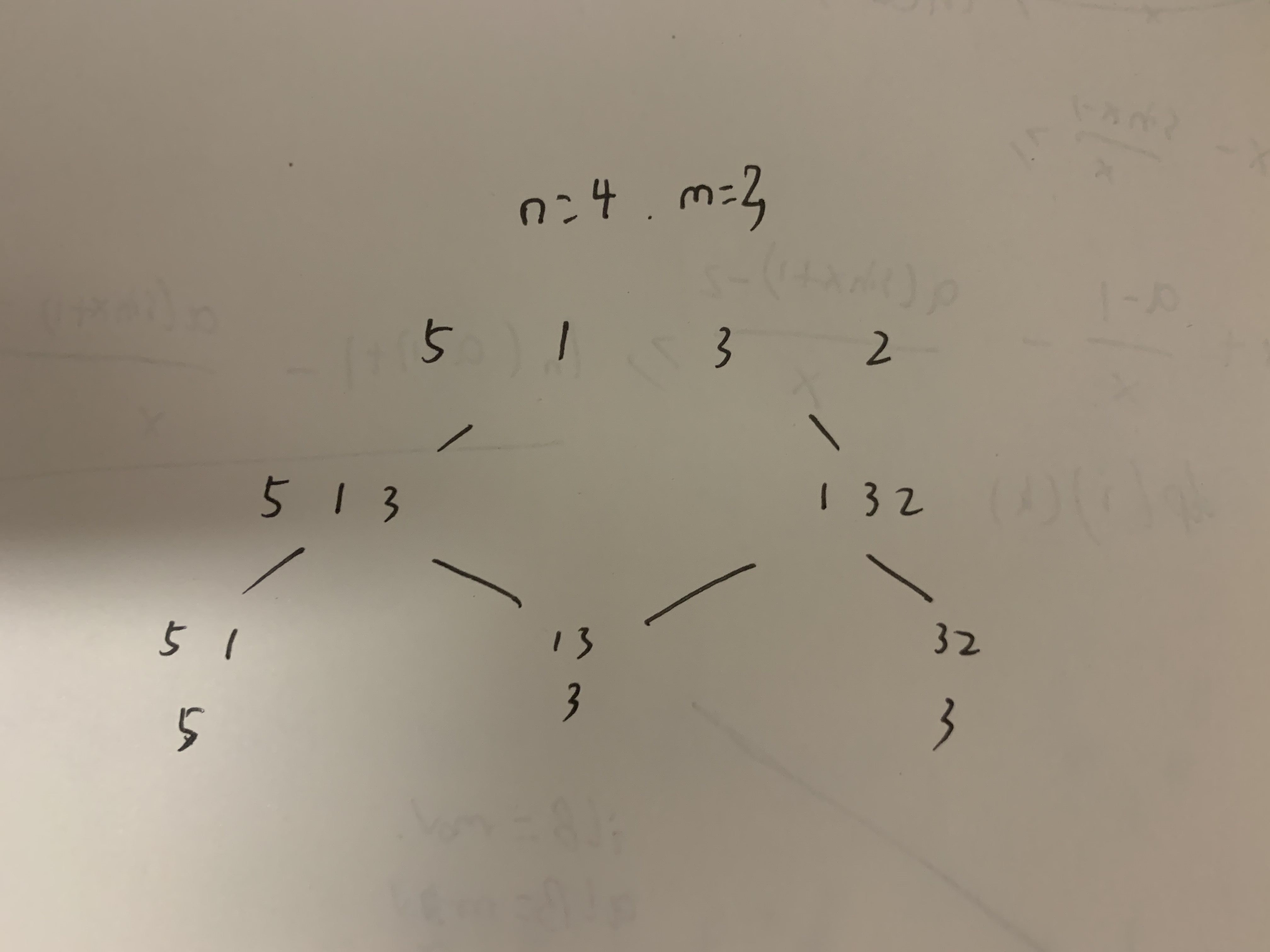
那么我们先把所有最终情况求出来,即(qwq[i]=max(a[i],a[i+n-m])),然后我们取连续的(m-k)个数求最小值,答案就是这些最小值中的最大值。
(O(n^2))暴力,(O(nlog_2 n))线段树或(ST)表,(O(n))单调队列都可以。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int kase; read(kase);
for (int ii = 1; ii <= kase; ii++) {
int n,m,k;
read(n);
read(m);
read(k);
k=min(k,m-1);
int a[n+1];
for(int i=1;i<=n;++i) read(a[i]);
int len=n-m;
deque<pair<int,int>> team;
int ans=0;
for(int i=1;i<=m;++i){
int qwq=max(a[i],a[i+len]);
while(!team.empty()&&team.front().second<i-m+k+1) team.pop_front();
while(!team.empty()&&team.back().first>=qwq) team.pop_back();
team.push_back(make_pair(qwq,i));
if (i>m-k-1) ans=max(ans,team.front().first);
}
write(ans,'
');
}
return 0;
}
D. Irreducible Anagrams (CF 1291 D)
题目大意
给定一个串(s),有(q)次询问,每次询问给定两个正整数(l,r),问子串(s[l...r])是否有一个不可约的同构串。两个串(s,t)互为同构串就是说(s)可以通过重新排列串(s)字母使得变为(t)。若存在一个串(t)是(s)的一个同构串,(t eq s),且(s)可以分为(k>1)个子串(s_1,s_2,...,s_k),(t)也相应位置分为(k>1)个子串(t_1,t_2,...,t_k),每个对应的子串(s_i,t_i)都是同构串,则(t)串是可约的,否则是不可约的。
解题思路
我们考虑一下一个串是否是可约的。
首先长度为一的串是不可约的,因为它无法分割成两部分或以上,前提为假命题为真。
然后一个串中只含有一个字母的也是不可约的,因为它的同构串只有它本身。
然后我们从字母出现的位置顺序考虑。如果一个(s)的同构串(t)是不可约的,那就意味着我无法将(s)分成两部分或以上,否则存在一个子串使得(s_i)和(t_i)不同构。换句话说,就是我在取(t)的前(k)位时,这前(k)位中出现的字母在(s)中出现的最远位置要大于(k),这才使得我要增大(k),才有可能使得(t)串的第一部分与(s)串的第一部分同构,而无法做到这一点就意味着我取了前(m)位时,这其中出现的字母在(s)中的最远距离已经是(s)的尾端,这就要我们把(s)取完,才使得(s)的第一部分与(t)的第一部分同构,而此时没有第二部分了,那么此时(t)就是个不可约的同构串。
从上面的思路我们就将问题转换成,这里有从左到右标号分别为(1)到(n)的(n)个格子,以及我们有(m)组数((m)个字母),每组数里有若干个从小到大排好的数(1leq aleq n)且各不相同(该字母出现的位置),共有(n)个数。现在要把这(n)个数放到(n)个格子里,对于一组数来说要先放小的数才能放大的数。问能否有一种放法,使得最大的数不在最后一个格子,且对于最大的数所在格子的前面每个格子(x),里面放的数满足(maxlimits_{1leq ileq x}(num_i)>x)。
最大的数所在的那一组中,如果最小的数不是(1),那么就一定存在该种放法,即我们直接把最大的数所在的那组数都放到前面的格子里即可。也就是说(s[l]!=s[r])时,就存在不可约的同构串。
而如果最小的数是(1),如果有两组的话,可以发现我们无法满足上述的条件,而如果有三组及以上,都可以满足。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
bool check(int pos[][26],int l,int r){
int cnt=0;
for(int i=0;i<26;++i)
cnt+=(pos[r][i]-pos[l-1][i])>0;
return cnt>2;
}
int main(void) {
char s[200006];
scanf("%s",s+1);
int n=strlen(s+1);
int pos[n+1][26]={0};
for(int i=1;i<=n;++i){
pos[i][s[i]-'a']++;
for(int j=0;j<26;++j)
pos[i][j]+=pos[i-1][j];
}
int q;
read(q);
for(int l,r,i=1;i<=q;++i){
read(l);
read(r);
if (l==r) puts("Yes");
else if (s[l]!=s[r]) puts("Yes");
else if (check(pos,l,r)) puts("Yes");
else puts("No");
}
return 0;
}