N句话题意
如果X=1, 表示第A个小朋友的糖果必须和第B个小朋友的糖果一样多;
如果X=2, 表示第A个小朋友的糖果必须少于第B个小朋友的糖果;
如果X=3, 表示第A个小朋友的糖果必须不少于第B个小朋友的糖果;
如果X=4, 表示第A个小朋友的糖果必须多于第B个小朋友的糖果;
如果X=5, 表示第A个小朋友的糖果必须不多于第B个小朋友的糖果;
求满足所有要求需要最少的糖果数(每个人至少为1)
一个差分约束题目,然额本蒟蒻还不是很会。首先分析限制条件,很明显2和4,3和5是一样的限制,并且要求最少的糖果数。那么不少于(多于)我们就建0边,而要求少于(多于)我们就建权值为1的边,很明显这样所需要的糖果最少。建好图后我们只需要跑一遍最长路即可。
为什么是最长路呢?看看下面这张图,(也是盗的)。
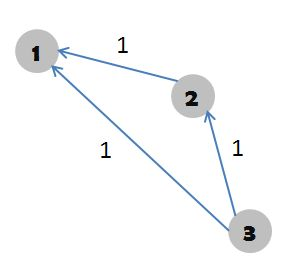
图中dis[1]如果是最短路为1,但很显然1点至少需要两个糖果。(很显然,因为肯定得满足约束最多的条件的情况才是合法的!)。
注:后面0向1→n建边时一定要倒序。
Coding
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int head[N],n,m,cnt;
struct limit
{
int to,next;
long long w;
}e[N*5];
void add(int x,int y,long long w)
{
e[++cnt].to=y,e[cnt].next=head[x],e[cnt].w=w;
head[x]=cnt;
}
int dis[N],tot[N];
long long vis[N];
queue<int> q;
bool SPFA()
{
q.push(0);
dis[0]=0;
vis[0]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
tot[u]++;
if(tot[u]==n-1) {cout<<-1; return 0;}
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].to;
if(dis[u]+e[i].w>dis[v])
{
dis[v]=dis[u]+e[i].w;
if(!vis[v]) q.push(v),vis[v]=1;
}
}
}
return 1;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x,y,opt;
scanf("%d%d%d",&opt,&x,&y);
if(opt==1) add(x,y,0),add(y,x,0);
if(opt==2)
{
if(x==y) {cout<<-1; return 0;}
add(x,y,1);
}
if(opt==3) add(y,x,0);
if(opt==4)
{
if(x==y) {cout<<-1; return 0;}
add(y,x,1);
}
if(opt==5) add(x,y,0);
}
for(int i=n;i;i--) add(0,i,1);
if(!SPFA()) return 0;
long long ans=0;
for(int i=1;i<=n;i++)
ans+=dis[i];
cout<<ans;
return 0;
}