半监督学习

监督式学习：全部使用含有标签的数据来训练分类器。

无监督式学习：具有数据集但无标签（即聚类）。

半监督学习：使用大量含有标签的数据和少量不含标签的数据进行训练分类或者聚类。

半监督学习：纯半监督学习和直推式学习

纯半监督学习和直推式学习的区别：

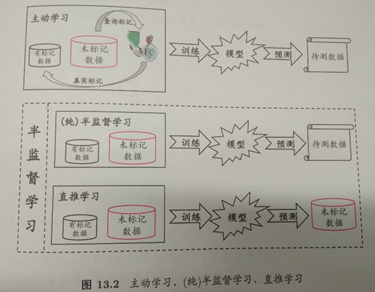
半监督学习在学习使并不知道最终的测试数据是什么，如下图：

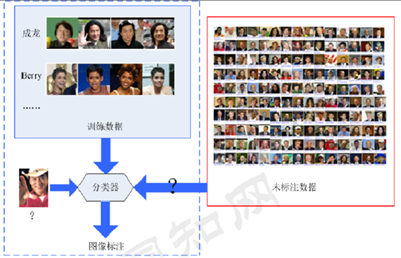
直推学习：假设未标记的数据就是最终要用来测试的数据，学习的目的就是在这些数据上取得最佳泛化能力。

半监督学习的两个假设

聚类假设：假设数据存在簇结构，同一个簇的样本属于同一个类别。

流行假设：假设数据分布在一个流行结构上，邻近的样本拥有相似的输出值。

两个假设的本质：相似的样本拥有相似的输出。

半监督学习的分类

基于生成模型的半监督学习方法：

基于协同训练的半监督分类方法：

基于低密度分离的半监督分类方法：

基于图的半监督学习方法：

最小分割Mincut、高斯随机场和调和函数CRF、谱图分割SGP、局部和全局一致性LGC、流形正则化MR、基于线性邻域的标记传播LNP等。

局部与全局一致性LGC算法： 

1、来源：D．Zhou，O．Bousquet，T．N．Lal,J．Westort,and B．Sch6ll【op￡Learning with local and global consistency．Advances in Neural Information Processing System 16，2004．

2、基本思想：让每个样本的标记信息迭代地向其邻近样本传播，直至到全局稳定状态。

3、目标函数：LGC的目标函数的特点是:（1）可以直接处理多分类问题;（2）正则化算子使用了归一化的拉普拉斯算子L=D^-1/2 LD^-1/2=I-D^-1/2 WD^-1/2来代替图拉普拉斯算子L=D-W;（3）损失函数的权重入为有限值，即采用软约束，从而使得算法对于错误的有标记数据有一定的容错能力。LGC的目标函数为:

 

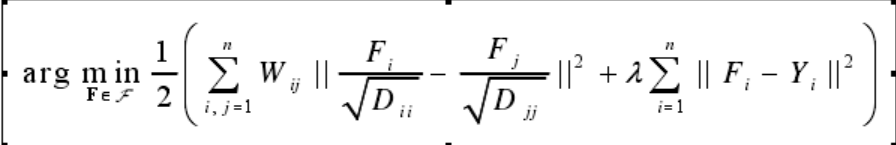
其中，F为调和函数，其在标注数据点上取值为其标识值，其在无标注数据点上的值为0；，Y为标签矩阵，W为相似度权重矩阵，D为度矩阵（对角矩阵），di=∑Wi ，为矩阵W的第i行元素之和。

前部分为正则化项，后者为损失函数。

损失函数：标签数据的标识和训练结果的标签的误差。

正则化项：相邻点W_ij的值越大，则f_i和f_j的值越相近。

4、实现步骤：（详细推导见西瓜书）

①构造邻接矩阵W，当i≠j时，高斯核函数W_ij=exp(-(x_i-x_j)²/2 ², W_ii=0

②计算矩阵S= D^-1/2 WD^-1/2，Dii=∑j wij ，

③迭代计算 F(t+1)=αSF(t)+(1-α)Y, α∈(0,1)， Y为标签矩阵，直至收敛。

 几种经典的图的构建

1、 全连接图

在全连接图中，所有结点之间都是有边连接的，而其边的权值通常是由高斯核函数计算得到的。

2、 近邻图

两种近邻图：k近邻和 近邻

在k近邻图中，每一个样本点与其最近的k个邻居点相连接，边的权值同样由高斯核函数计算得到。

在 近邻图中，数据点之间的连接发生在半径为 的近邻范围内，即若结点i和j之间的距离d(i,j)＜ ，则结点i,j之间有边连接。

3、 局部自适应图

4、 L1-图