树（1）------实现和遍历

1、树的性质：

（1）树是分层的，分层的意思是树的顶层部分更加宽泛一般底层部分更加精细具体。

（2）一个节点（node)的所有子节点(children）和另一个节点的子节点是完全独立的。

（3）它的每个叶子节点（leaf)都是不同的。

2、相关概念：

节点、边、根节点、路径、父节点、兄弟节点、……

3、树的实现

（1）嵌套列表

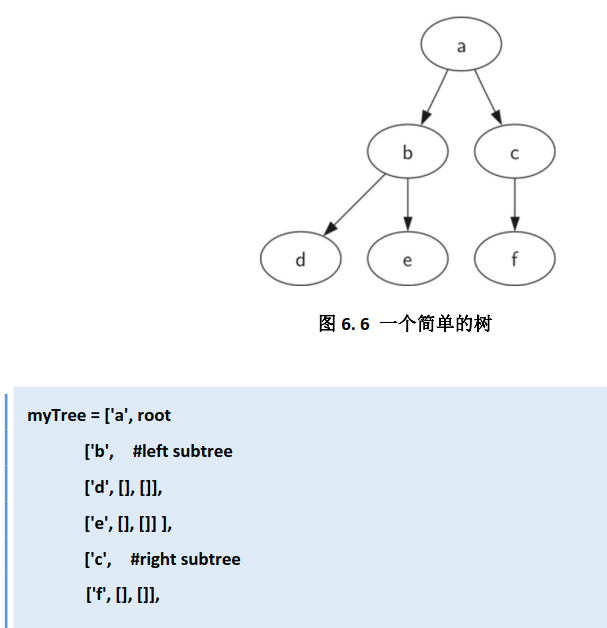
def BinaryTree(r):
    return [r,[],[]]
def insertLeft(root,newBranch):
    t=root.pop(1)
    if len(t)>1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch,[],[]])
    return root
def insertRight(root,newBranch):
    t=root.pop(2)
    if len(t)>1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root
def getRootVal(root):
    return root[0]
def setRootVal(root,newVal):
    root[0]=newVal
def getLeftChild(root):
    return root[1]
def getRightChild(root):
    return root[2]

r=BinaryTree('a')
insertLeft(r,'b')
insertRight(r,'c')
insertRight(r[1],'d')
insertLeft(r[2],'e')
insertRight(r[2],'f')
print(r)
I=getLeftChild(r)
print(I)

（2）节点和引用

class BinaryTree:
    def __init__(self,rootObi):
        self.key=rootObi
        self.leftChild=None
        self.rightChild=None
    def insertLeft(self,newNode):
        if self.leftChild==None:
            self.leftChild=BinaryTree(newNode)
        else:
            t=BinaryTree(newNode)
            t.leftChild=self.leftChild
            self.leftChild=t
    def insertRight(self,newNode):
        if self.rightChild==None:
            self.rightChild=BinaryTree(newNode)
        else:
            t=BinaryTree(newNode)
            t.rightChild=self.rightChild
            self.rightChild=t 
    def getRightChild(self):
        return self.rightChild
    def getLeftChild(self):
        return self.leftChild
    def setRootVal(self,obj):
        self.key=obj
    def getRootVal(self):
        return self.key

r=BinaryTree('a')
print(r.getRootVal())
print(r.getLeftChild())
r.insertLeft('b')
r.insertRight('c')
r.insertLeft('d')
r.insertRight('e')
print(r.getRootVal())
print(r.getLeftChild().getLeftChild().getRootVal())
print(r.getRightChild().getRightChild().getRootVal())

4、树的遍历

前序遍历：中，左，右

中序遍历：左，中，右

后序遍历：左，右，中

前序遍历：

def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild())

#放入上面类中的代码
def preorder(self):
    print(self.key)
    if self.leftChild:
        self.leftChild.preorder()
    if self.RightChild:
        self.RightChild.preorder()
#非递归
def pre1(root):
        if not root:
            return []
        res = []
        stack = [root]
        while stack:
            node = stack.pop()
            res.append(node.val)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return res

后序遍历：

def postorder(tree):
    if tree:
        postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
        print(tree.getRootVal())

#非递归
113 void posOrderUnRecur2(Node *head)
114 {
115     if(NULL != head)
116     {
117         stack<Node*> s;
118         s.push(head);
119         Node *cur = NULL;
120         while(!s.empty())
121         {
122             cur = s.top();
123             if(NULL != cur->left && head != cur->left && head != cur->right)
124                 s.push(cur->left);
125             else if(NULL != cur->right && head != cur->right)
126                 s.push(cur->right);
127             else
128             {
129                 cout << s.top()->value << " ";
130                 s.pop();
131                 head = cur;
132             }
133         }
134     }
135     cout << endl;
136     return ;    
137 
138 }

中序遍历：

def inorder(tree):    
    if tree:
        inorder(tree.getLeftChild())
        print(tree.getRootVal())
        inorder(tree.getRightChild())

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        '''
        ######递归
        res=[]
        left=[]
        right=[]
        if root:
            left=self.inorderTraversal(root.left)
            res.append(root.val)
            right=self.inorderTraversal(root.right)
        return left+res+right
        '''
        ###非递归
        if not root:
            return []
        stack = []
        node = root
        res = []
        while stack or node:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack.pop()
                res.append(node.val)
                node = node.right
        return res
            

 

 

5、堆（最小堆、最大堆）

python模块：from pythonds.trees.binheap import BinHeap