算法53----换钱的最小次数和方法数【动态规划】

 

---

一、题目：换钱的最小次数

  给定数组arr,arr中所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张，再给定一个整数aim代表要找的钱数，求组成aim的最少货币数。

  举个例子
  arr[5,2,3] ,aim=20
 　　4张5元可以组成20,并且是最小的，所以返回4
  arr[5,2,3],aim=0。
  　　不用任何货币就可以组成0元，这里返回0.
  arr[5,2,3],ami=4
  　　这里无法组成返回-1

思路：时间和空间都为O（M*aim)【len(arr) = M 】

dp 矩阵为：大小为M*aim

dp[i][j]的含义是在可以任意使用arr[0…i]货币的情况下，组成j所需的最小张数，矩阵的每一行和每一列可以先确定，其他的位置dp[i][j] = min( dp[i-1][j] , dp[i][j-arr[i]]+1)。

dp的第一行表示：只用 5 来分别构成 0……20 最少要多少张，比如 5 需要 1张，10需要2张，……构不成的赋系统最大值，最后返回-1。

dp的第二行表示：只用5和2分别构成0到20 最少要多少张。

dp的第三行表示：只用5，2，3分别构成0到20最少要多少张。

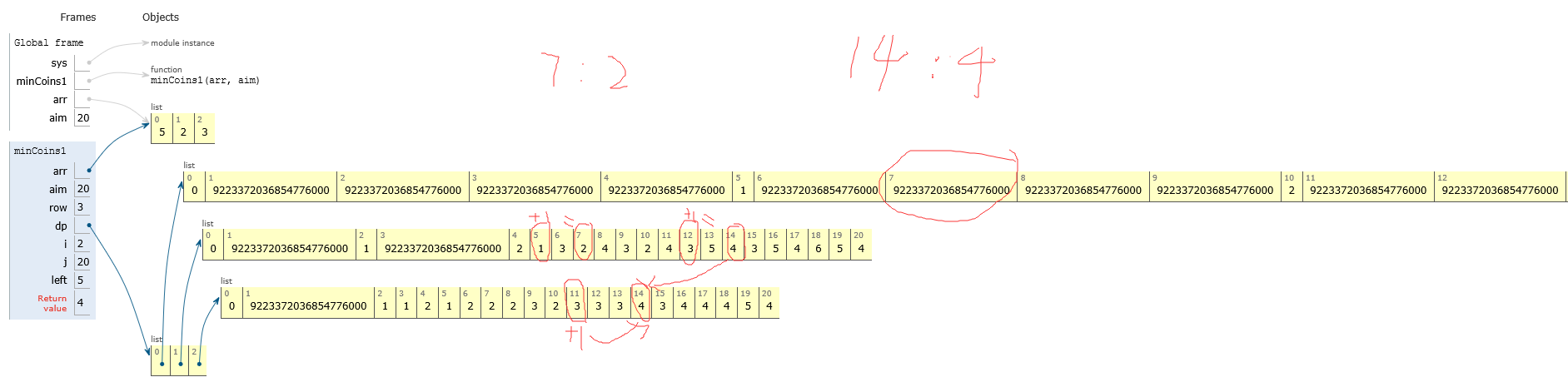
dp矩阵的构建：初始化系统最大值

• 第一列都为0，因为0不需要任何币来构成。
• 第一行：能被5整除的赋值，值为整除的数。比如：5赋值1，10赋值2，15赋值3，20赋值4。
• 第二行、第三行……：

1. 比如：dp 第2行第7列的值 2 是根据
2. dp [7-2] +1 = 1 +1 =2来的，即【7可以由1个5和1个2组成】，
3. 但是还要看第一行7列的值是不是更小，即 dp [i][j] = min( dp [j-arr[i]] +1，dp [i-1][j] ），dp [j-arr[i]] +1不能是系统最大值。

 代码1：

import sys
def minCoins1(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return -1
    row = len(arr)
    dp = [[sys.maxsize for i in range(aim+1)] for j in range(row)]
    for i in range(row):
        dp[i][0] = 0
    for j in range(1, aim+1):
        if j % arr[0] == 0:
            dp[0][j] = j // arr[0]
    for i in range(1, row):
        for j in range(1, aim+1):
            left = sys.maxsize
            if j - arr[i] >= 0 and dp[i][j-arr[i]] != sys.maxsize:
                left = dp[i][j-arr[i]] + 1
            dp[i][j] = min(left, dp[i-1][j])
    return dp[row-1][aim] if dp[row-1][aim] != sys.maxsize else -1
arr = [5,2,3]
aim = 20
minCoins1(arr, aim)

 代码2：时间为O（M*aim)【len(arr) = M 】，空间为O（aim+1)，dp 大小为 aim+1的列表

#经过空间压缩的动态规划
def minCoins2(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return -1
    row = len(arr)
    dp = [sys.maxsize for i in range(aim+1)]
    dp[0] = 0
    for i in range(1, aim+1):
        if i % arr[0] == 0:
            dp[i] = i // arr[0]
    for i in range(1, row):
        dp[0] = 0
        for j in range(1, aim+1):
            left = sys.maxsize
            if j - arr[i] >= 0 and dp[j-arr[i]] != sys.maxsize:
                left = dp[j-arr[i]] + 1
            dp[j] = min(left, dp[j])
    return dp[aim] if dp[aim] != sys.maxsize else -1

---

题目二：换钱的方法数

https://blog.csdn.net/qq_34342154/article/details/77122125

给定数组arr，arr中所有的值都为整数且不重复。每个值代表一种面值的货币，每种货币有无数张，再给定一个整数aim代表要找的钱数，求换钱的方法有多少种。

思路1：暴力递归，最坏情况下时间O(aim^N)，N表示数组的长度

首先介绍暴力递归的方法。如果arr = [5, 10, 25, 1]，aim = 1000，分析过程如下：

用０张５元的货币，让[10, 25, 1]组成剩下的1000，最终方法数记为res1。
用１张５元的货币，让[10, 25, 1]组成剩下的995，最终方法数记为res2。
用２张５元的货币，让[10, 25, 1]组成剩下的990，最终方法数记为res3。
……
用201张５元的货币，让[10, 25, 1]组成剩下的0，最终方法数记为res201。

那么res1 + res2 + res3 + …… +res201的值就是中的方法数。

#暴力递归方法
def coins1(arr, aim):
    def process1(arr, index, aim):
        if index == len(arr):
            return 1 if aim == 0 else 0
        else:
            res = 0
            for i in range(0, aim//arr[index]+1):
                res += process1(arr, index+1, aim-arr[index]*i)
        return res


    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    return process1(arr, 0, aim)

思路2：记忆搜索：时间复杂度为O(N*aim^2)，空间复杂度O(N*aim)。

采用一个字典存储计算过的结果，暴力递归会重复计算结果。比如使用0张5元+1张10元的情况和使用2张5元+0张10元的情况，都需要求[25, 1]组成剩下的990的方法数。记忆搜索就是使用一张记录表将递归过程中的结果进行记录，当下次再遇到同样的递归过程，就直接使用表中的数据。

 

第三行：圈出的

第一步：当0个5：当0个2，只用【3】构成15的方法：1个

　　　　　　　　　1个2，只用【3】构成13的方法：-1个【不可能】

　　　　　　　　　2个2，……

　　　　　　　　　……

　　　　　　　　　7个2……

第三行：圈出的

第二步：当1个5时，当0个2，只用【3】构成10：-1个

　　　　　　　　　    1个2，只用【3】构成8：-1个

　　　　　　　　　　……

　　　　　　　　　　5个2，只用【3】构成0：1个

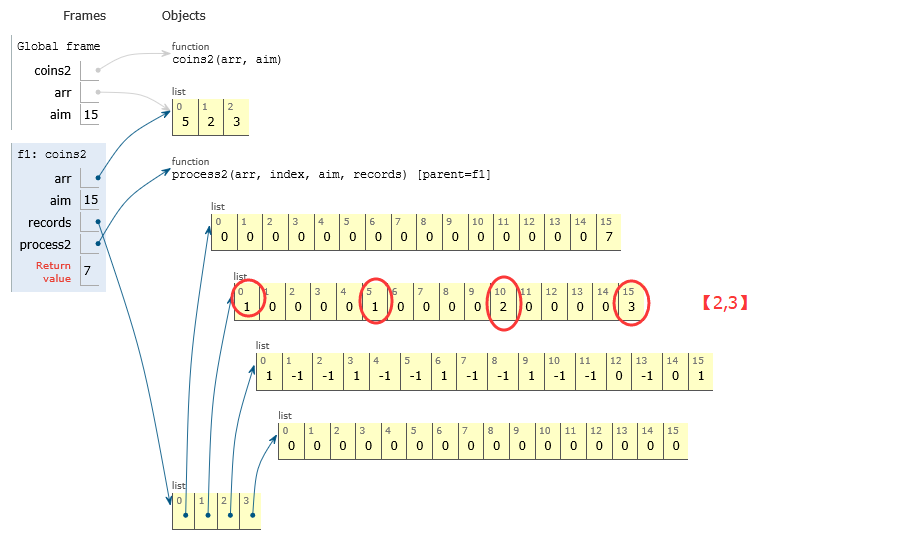
第二行：

当0个5时：只用【2，3】构成15有3种方法

当1个5时：只用【2，3】构成10有2种方法

当2个5时：只用【2，3】构成5有1种方法

当3个5时：只用【2，3】构成0有1种方法

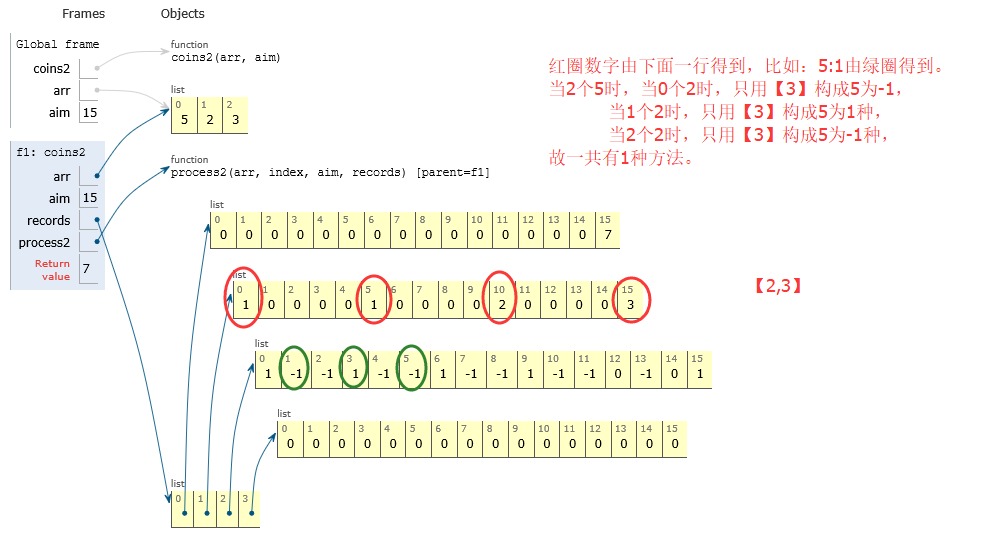
第一行：结果，用【5，2，3】构成15有7种方法

 代码：

def coins2(arr, aim):
    def process2(arr, index, aim, records):
        if index == len(arr):
            return 1 if aim == 0 else 0
        else:
            res = 0
            for i in range(0, aim//arr[index]+1):
                mapValue = records[index+1][aim-arr[index]*i]
                if mapValue != 0:
                    res += mapValue if mapValue != -1 else 0
                else:
                    res += process2(arr, index+1, aim-arr[index]*i, records)
        records[index][aim] = -1 if res == 0 else res
        return res


    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    records = [[0 for i in range(aim+1)] for j in range(len(arr)+1)]
    return process2(arr, 0, aim, records)
arr = [5,2,3]
aim = 15
res1 = coins2(arr,aim)

 思路3：动态规划：时间O（M*aim^2)，空间O（M*aim）

 

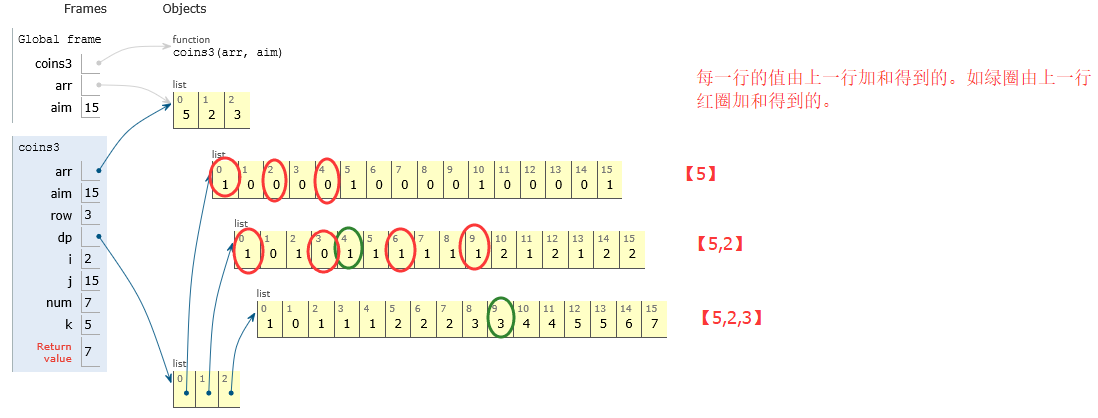
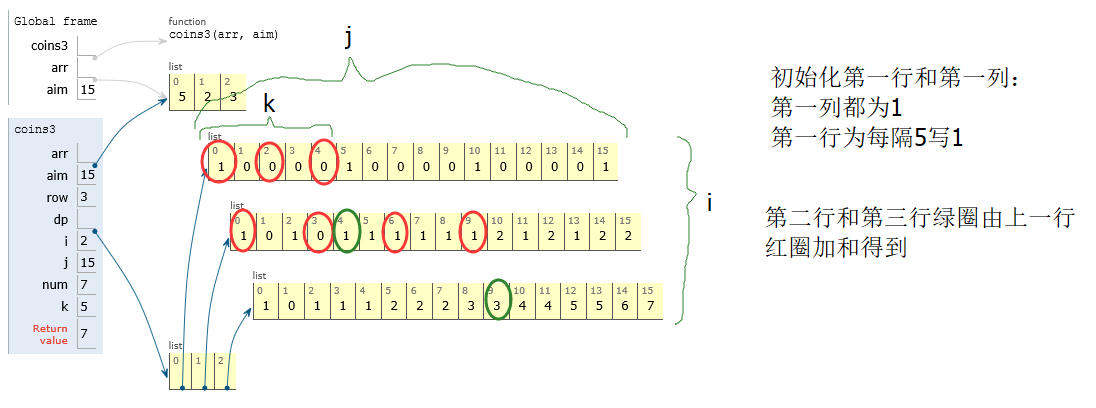
为何绿圈等于上一行红圈的加和？即num += dp[i-1][j-arr[i]*k]

比如绿圈的第二行第5列那个1：只用【5，2】

上一行红圈表示只用【5】构成0，2，4的方法数为1，0，0

则当用0个2时，对应【5】构成4方法数为0

当用1个2时，对应【5】构成2方法数为0

当2个2时，对应【5】构成0方法数为1

代码：

def coins3(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    row = len(arr)
    dp = [[0 for i in range(aim+1)]for j in range(row)]
    for i in range(row):
        dp[i][0] = 1
    for j in range(1, aim//arr[0]+1):
        dp[0][arr[0]*j] = 1
    for i in range(1, row):
        for j in range(1, aim+1):
            num = 0
            for k in range(j//arr[i]+1):
                num += dp[i-1][j-arr[i]*k]
            dp[i][j] = num
    return dp[row-1][aim]

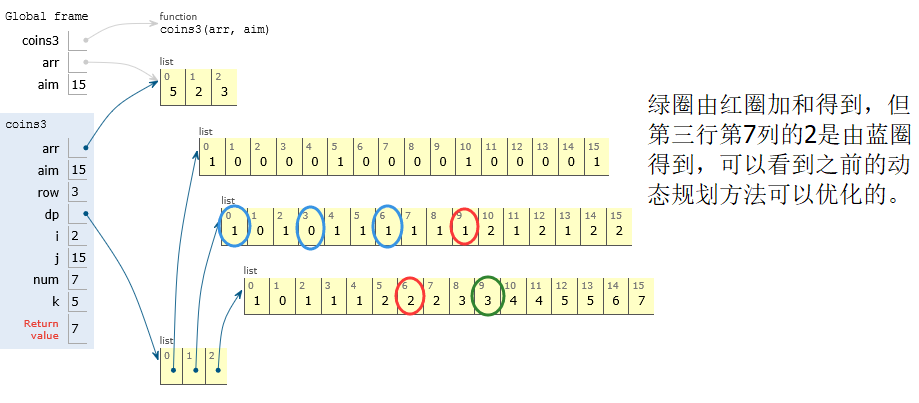
思路4：动态规划时间的优化：时间O（M*aim)，空间O（M*aim）

思路3中的第三步循环k可省略。

for k in range(j//arr[i]+1):
          num += dp[i-1][j-arr[i]*k] 即

dp[i][j] = dp[i-1][j] + dp[i-1][j-arr[i]] + dp[i-1][j-2*arr[i]] + …dp[i-1][j-k*arr[i]]

等价于

dp[i][j] = dp[i-1][j] + dp[i][j-arr[i]]

代码：

def coins4(arr, aim):
    if arr == None or len(arr) == 0 or aim < 0:
        return 0
    row = len(arr)
    dp = [[0 for i in range(aim+1)] for j in range(row)]
    for i in range(row):
        dp[i][0] = 1
    for j in range(1, aim//arr[0]+1):
        dp[0][arr[0]*j] = 1
    for i in range(1,row):
        for j in range(1, aim+1):
            dp[i][j] = dp[i-1][j]
            dp[i][j] += dp[i][j-arr[i]] if j-arr[i] >= 0 else 0
    return dp[row-1][aim]

思路5：动态规划空间的优化：时间O（M*aim)，空间O(aim)。

def coin5(arr,aim):
    if not arr or not aim:
        return 0
    dp = [0] * (aim + 1)
    for i in range(0,aim+1,arr[0]):
        dp[i] = 1
    for i in range(1,len(arr)):
        for j in range(1,aim+1):
            dp[j] += dp[j-arr[i]] if j - arr[i] >= 0 else 0
    return dp[-1]
arr = [5,2,3]
aim = 15
coin5(arr,aim)

---

题目三、0-1背包

m个物品价值为 p[m]，体积为 w[m]，现有一个容量为 v 的背包，怎么装物品价值最大?

思路：

m[i][j] = max{m[i - 1][j], m[i - 1][j - w[i]] + v[i]}     j >= w[i];           

         = m[i - 1][j]                                                    j < w[i];

解释：

当我们依次从package 里面取到第 i 个物品的时候，我们可以在前 i 个物品中，得到一个最优解。而每一次遍历，如下

如果当前物品大于背包的容积，这个物品太大了，包塞不下。那么最优解就是前n-1件物品放进这个背包的最大价值。
arr[i][j] = arr[i-1][j]

如果当前物品不大于背包的容积，这个物品可以塞下，需要重新开始计算，当前 i 物品组合的最大价值。分为两种情况，该物品放还是不放。
2.1 不放的话，和上面的公式相同； 
2.2 放的话，则背包容量减去第n件物品的重量，再去装前 i-1 件物品，所得的最大价值。两种情况中较大的就是最优解。
arr[i][j] = max (arr[i-1][j] , arr[i-1][j -v[i]]+ cost[j])

 

 

题目四：硬币翻转

有 N 个硬币，一开始全部正面朝上，每次可以翻转 M 个硬币（ M 小于 N ），使得最终所有硬币反面朝上。

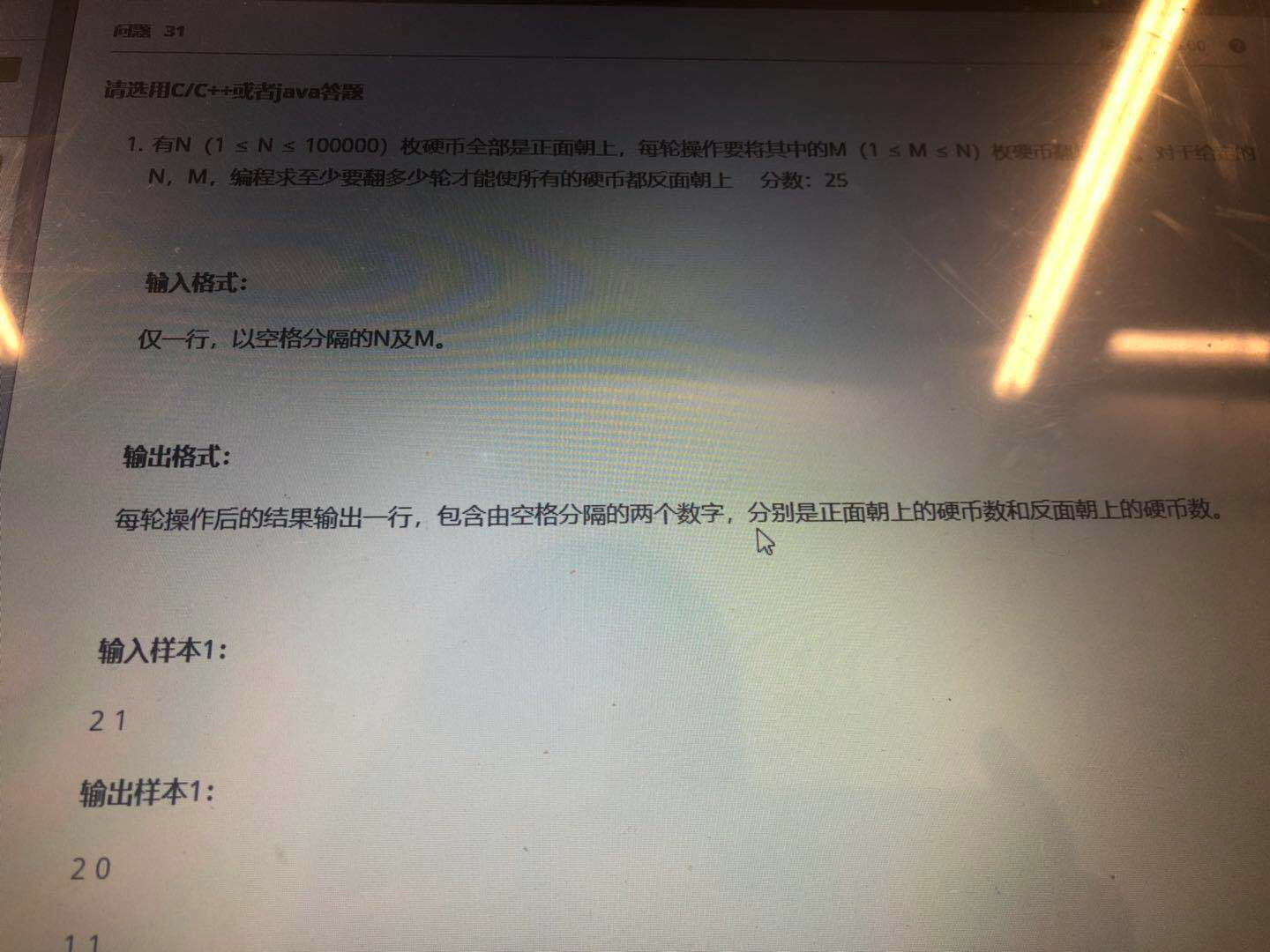
输入：2 1

输出：

2 0
1 1
0 2

输入：5 3

5 0
2 3
1 4
4 1
3 2
0 5

输入：5 5

5 0

0 5

输入：5 4

No Solution

思路：

　　采用【1，1，1，1……】来作为硬币正面，反面就变为0，每M个就变为0。

代码：

　　

def test(N,M):
    arr = [1] * N
    if not M % 2:
        print('No Solution')
    else:
        index = 0
        while 1 in arr:
            num1 , num2 = 0 , 0
            for i in range(len(arr)):
                if arr[i] == 1:
                    num1 += 1
            num2 = N - num1
            print(num1,num2)
            end = index + M - N if (index + M - N)>0 else (index + M)
            if index <= end:
                for i in range(index,end):
                    arr[i] = 1- arr[i]
            else:
                for i in range(0,end):
                    arr[i] = 1-arr[i]
                for i in range(index,N):
                    arr[i] = 1-arr[i]
            index = end
        print(0,N)
N , M = input().split()
N,M = int(N),int(M)
test(N,M)