算法54---动态规划

一、啥问题可以用动态规划来解决【采用空间来存储重复计算的结构】

1. 最优子结构：就是原问题可以分为多个子问题。
2. 重复子问题：子问题在计算过程中是重复计算的。

举例子：斐波那契问题：F（n) = F（n-1) + F (n-2)

F（n)分为两个子问题：F（n-1)和F（n-2)，

而F（n-1)和F（n-2)重复计算了F（n-2)部分，所以这两个问题就是重复子问题

重复子问题可以用空间来存储计算过的值，当在计算过程中重复使用的时候就可以在存储表中取值。

二、例子解析：

• 斐波那契/爬楼梯：f(1) = 1,f(2)=2，f(n) = f(n-1)+f(n-2)。
• 最短路径：dp[i][j]表示第i行第j列的最短路径值。

子问题：dp[i][j] 可分为 dp[i][j-1] 和 dp[i-1][j]两个子问题。

状态方程：dp[i][j] = min(dp[i][j-1],dp[i-1][j]) + grid[i][j]

• 龙下城游戏：dp[i[[j]：如果骑士要走上位置（i,j)，并且从该位置选一条最优的路径，最后走到右下角，骑士起码应具备的血量。最终结果为dp[0][0]。

子问题：dp[i][j+1]、dp[i+1][j]

状态方程：

如果骑士向右选择，dp[i][j]_1  = max{ dp[i][j+1] - map[i][j] , 1}     

如果骑士向下选择，dp[i][j]_2  = max{ dp[i+1][j] - map[i][j] , 1}     

dp[i][j] = min{ dp[i][j]_1, dp[i][j]_2}

•  三角形的最小路径和：dp【i】【j】：表示第i行第j列时最短路径。

子问题：邻近的两个：dp[i-1][j-1]、dp[i-1][j]

状态方程：dp[i][j] = min(dp[i-1][j-1],dp[i-1][j]) + triangle[i][j]

• 下降路径最小和：dp[i][j] ：表示第i行第j列时最短下降路径。

子问题：dp[i-1][j-1]、dp[i-1][j+1]、dp[i-1][j]

状态方程：dp[i][j] = min(dp[i-1][j-1], dp[i-1][j+1], dp[i-1][j] ) + A[i][j]

 

• 有障碍的路径数量【不同路径II】：dp[i][j] 表示从左上角走到第i行第j列位置时的路径数量。

子问题：dp[i-1][j]、dp[i][j-1]

状态方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]

• 打家劫舍：dp【i】表示第 i 家时最高金额

状态方程：dp【i】 = min(dp[i-1] , dp[i-2] + nums[i] )

• 使用最小花费爬楼梯：

状态方程：dp[0] = 0,dp[1] = cost[0]

dp[i] = min(dp[i-1],dp[i-2]) + cost[i]

• 石子游戏：dp[i][j]表示：表示在piles中下标 i 至下标 j 之间的玩家1 所拿石子总数和 玩家2所拿石子总数之差。dp[i][j] > 0 表明玩家1赢，输出True

状态方程：dp[ i ][ j ] = piles[ i ]（初始）

dp[ i ][ j ] = max( piles[ i ] - dp[ i+1 ][ j ], piles[ j ] - dp[ i ][ j-1 ])

• 换钱的最小次数：dp[i][j] 表示 arr[0:i] 构成 j 元钱的最小次数。

子问题：dp[i][j] 可分为 dp [j-arr[i]] 和 dp [i-1][j]两个子问题。

状态方程：dp [i][j] = min( dp [j-arr[i]] +1，dp [i-1][j] ）

• 换钱的总共方法数：dp[i][j] 表示 arr[0:i] 构成 j 元钱的总共方法数。

子问题：dp[i][j] 可分为 dp [j-arr[i]] 和 dp [i-1][j]两个子问题。

状态方程：dp[i][j] = dp[i][j-arr[i]] + dp[i-1][j]

• 最长公共子序列：c[i][j]表示(x1,x2....xi) 和 (y1,y2...yj) 的最长公共子序列的长度。

原问题：c[i][j]

子问题：当两个序列的最后一个元素相等，即X_i =Y_j，则❶c[i-1][j-1]   

　　　　否则当 X_i ≠Y_j， ❷c[i][j-1]   ❸c[i-1][j]

状态方程：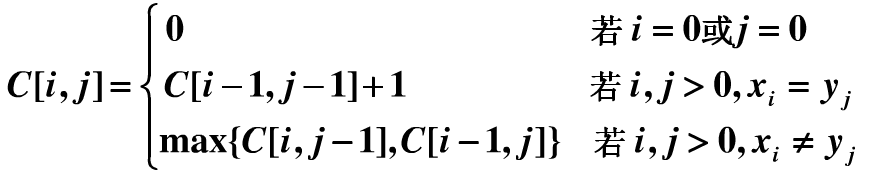

• 最长递增子序列：dp[j] 以列表中第 j 项结尾的最长递增子序列的长度.

原问题：给定一个数列，长度为N，设 dp[j] 为：以数列中第 j 项结尾的最长递增子序列的长度，求max(dp).

子问题：对 dp[j] 来讲，dp[0]……dp[j-1] 都是 dp[j] 的子问题

状态方法：dp(j) = { max(dp(i)) + 1, i<j且L[i]<L[j] }

• 最长公共子串：dp[i][j]用来记录具有这样特点的子串——结尾同时也为子串x1x2⋯xi与y1y2⋯yj的结尾的长度。

子问题：c[i-1][j-1]

 

状态方法：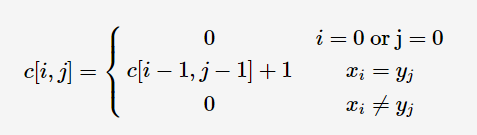

• 两个字符串的最小ASCII删除和：dp[i][j]表示s1字符串第i个到s2字符串di第j个相等所需的代价。

状态方程：如果s1[i] == s2[j]: dp[i][j] = dp[i-1][j-1]

否则：dp]i][j] =  dp[i][j] = min(dp[i][j-1] +ord(s2[j-1]),dp[i-1][j] + ord(s1[i-1]),dp[i-1][j-1] + ord(s1[i-1])+ord(s2[j-1]))

• 最小编辑代价：dp[i][j]表示str1[0......i-1]编辑成str2[0......j-1]的最小编辑代价。

子问题：dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]

状态方法：dp[i][j] = min( dp[i][j-1]+ic , dc+dp[i-1][j] , dp[i-1][j-1] + rc 【如果str1[i-1]==str2[j-1]，rc = rc，否则，rc = 0】）

• 交错字符串：dp[i][j] 代表是s1的前i个字符与s3中匹配，s2中前j个字符与s3中匹配.

子问题：dp[i-1][j]、dp[i][j-1]

状态方法：dp[i][j] = (dp[i-1][j] == True and s1[i-1] == s3[i+j-1]) or (dp[i][j-1] ==True and s2[j-1] == s3[i+j-1])

• 等差数列划分：找规律
• 丑数：t1,t2,t3三个变量记录乘以2，3，5的个数。
• 完全平方数：

状态转移方程：F（n） = min{ F(n-ai) + 1 } 其中ai为小于等于n的完全平方数

• 计算各个位数不同的数字个数：dp[i]表示 i 位数范围内【0，10^i】各位数字都不同的数字 x 的个数。

状态方程：dp[i] = dp[i-1] + fi，

　　记 f( n )为 [ 0, 10^n )范围内满足条件的数值个数，记 g( k ) 为 k位数中满足条件的数值个数， 则 f(n) = g(1) + g(2) + g(3) + ... +g(n) = f (n - 1) + g (n)，

• 环绕字符串中唯一的子字符串【动态规划】：dp【i】表示以26个字母中第i个字母作为结尾的连续子串个数。dp[0] 表示以a为结尾的，dp[1]表示以b为结尾的……。

我们看abcd这个字符串，

以a为结尾的子字符串为a，dp[0] = 1

以b为结尾的子字符串为b，ab 。dp[1] = 2

以c为结尾的子字符串为c，bc，abc。dp[2] = 3

以d结尾的子字符串有abcd, bcd, cd, d，故 i = 3，dp[3] = 4。

结果为：1+2+3+4 = 10

题目可以转换为分别求出以每个字符(a-z为结束字符的最长连续字符串就行了，我们用一个数组res记录下来，最后在求出数组res的所有数字之和就是结果。

•  n个学生成绩排名，a>b>c……，a>b=c，有多少种排名。dp[j] = (j+1) * (dp[j-1] + dp[j])