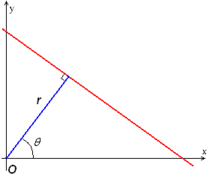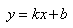
过某一点(x0,y0)的所有直线的参数都会满足方程y0=kx0+b,在k-b空间中,以一个点表示。
一条直线在图像中是一系列离散点的集合,通过一个直线的离散极坐标公式,可以表达出直线的离散点几何等式如下:

X *cos(theta) + y * sin(theta) = r
其中角度theta指r与X轴之间的夹角,r为到直线几何垂直距离。任何在直线上点,x, y都可以表达,其中 r, theta是常量。
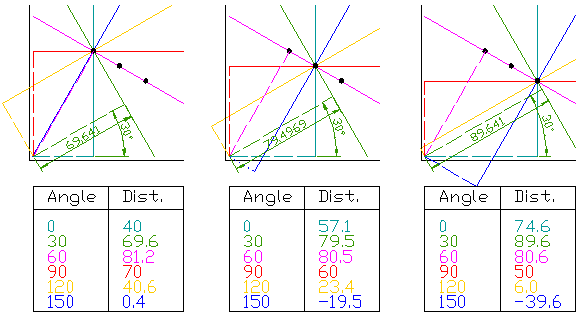
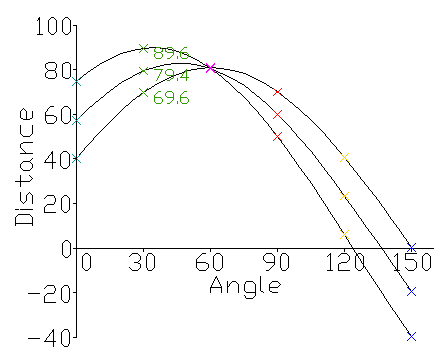
r, theta则是我们要寻找 的变量。
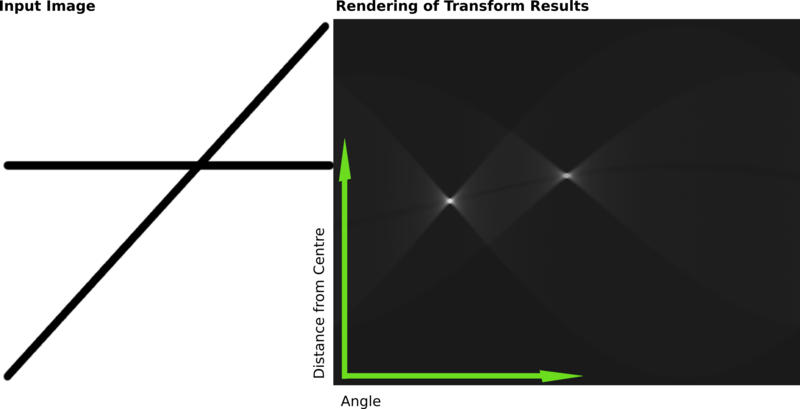
如果我们能绘制每个(r, theta)值根据像素点坐标P(x, y)值的话,那么就从图像笛卡尔坐标系统转换到极坐标霍夫空间系统,这种从点到曲线的变换称为直线的霍夫变换。
变换通过量化霍夫参数空间为有限个值间隔等分或者累加格子。当霍夫变换算法开始,每个像素坐标点P(x, y)被转换到(r, theta)的曲线点上面,累加到对应的格子数据点,当一个波峰出现时候,说明有直线存在。同样的原理,我们可以用来检测圆,只是对于圆的参数方程变为如下等式:
(x –a ) ^2 + (y-b) ^ 2 = r^2
其中(a, b)为圆的中心点坐标,r圆的半径。这样霍夫的参数空间就变成一个三维参数空间。