寻找两个已序数组中的第k大元素

寻找两个已序数组中的第k大元素

1、问题描述

　　给定两个数组与，其大小分别为、，假定它们都是已按照增序排序的数组，我们用尽可能快的方法去求两个数组合并后第大的元素，其中，。例如，对于数组，。我们记第大的数为，则时，。这是因为排序之后的数组，第4大的数是4。我们针对这一个问题进行探讨。

2、算法一

　　第一眼看到这个题的时候，我们能够很快地想出来最基本的一种解法：对数组和进行合并，然后求出其第大的数，即找到答案。合并的过程，我们可以参考归并排序的合并子数组的过程，时间复杂度为。下面给出算法：

 

int findKthMaxNumOfArrays(int *a,int m,int *b,int n,int k)
{
    int *p=a;
    int *q=b;
    int i=0;
    int j=0;
    int cur=0;
    while(i<m&&j<n)
    {
        if(a[i]<b[j])
        {
            cur++;
            if(cur==k) return a[i];
            i++;
        }
        else 
        {
            cur++;
            if(cur==k) return b[j];
            j++;
        }
    }
    while(i<m)
    {
        cur++;
        if(cur==k) return a[i];
        i++;
    }
    while(j<n)
    {
        cur++;
        if(cur==k) return b[j];
        j++;
    }
}

3、算法二

　　实际上算法一的时间复杂度已经是线性的了。可是，是否存在更快的算法能够完成这项任务呢？答案是肯定的，时间复杂度可以缩短到时间内。在这种算法中，二分的思想十分重要。我们将数组分为两半，前一部分的大小为，后一部分为；数组同时分为这样两部分，第一部分的大小为，第二部分的大小为。如下图所示：

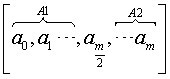
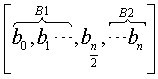
通过与，我们将每个数组分为2部分，分别记为、和、。假定，如果不是，我们只需要交换、两个数组即可。接下来，我们看第大的数落在了哪个区间里面，令，这个实际上是包含了，，。如果时，则说明肯定不在里面，这是由于：中的所有数，而中的所有数与，而这部分数总共有个，说明是第个，若出现在中，则说明，与假设矛盾。我们可以得出该结论。因此，在判断之后，我们可以剔除数组的部分，然后再在新数组中寻找；另外，如果，则说明肯定不在部分，这部分的证明同上一个证明相同，不再赘述。同样地，在判断之后，我们可以剔除数组的部分，然后再在新数组中寻找。基于这样一种思想，我们每次迭代，都删除了其中一个数组中一半的元素，时间复杂度大约可认为是。

　　在实现的时候，我们需要特别注意边界条件，详细的代码如下：

 

int findKthMaxNumOfArrays(int *A, int m, int *B, int n, int k)
{
        if(m == 0)return B[k-1];
        if(n == 0)return A[k-1];
        int i = m>>1, j = n>>1, *p, *q, t;
        if(A[i] <= B[j])p = A, q = B;
        else p = B, q = A, swap(i, j), swap(m, n);
        t = i + j + 1;
        if(t >= k)return func(p, m, q, j, k);
        else if(t < k)return func(p+i+1, m-i-1, q, n, k-i-1);
    }

4、扩展问题

　　通过算法二，我们很容易地解决一个类似的问题：求两个已序数组,的中位数。所谓的中位数，对于一个有个元素的已序数组，如果是奇数，则中位数是第个元素的值；如果是偶数，则它的中位数是第与第数的平均值。对于为奇数，则利用算法二求第个元素的值即可，对于为偶数，利用算法二求第个与第个元素的值，求其平均值即可。

　　对于这个问题，在LeetCode中有另外一种解法，但是阅读后发现其需要处理的个别case太多，相比而言没有本文所介绍的算法简洁。如果想要了解，给出链接：http://leetcode.com/2011/03/median-of-two-sorted-arrays.html。

作者：Chenny Chen 
出处：http://www.cnblogs.com/XjChenny/ 
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

 

分类: 数据结构与算法