查找树是一种支持包括查找、插入、找最小值、找出最大值、找出前趋、找出后继、删除动态集合操作的数据结构。
基本操作的时间与树的高度成正比,对于一棵含有n个结点的完全二叉树,基本操作的最坏情况运行时间为Θ(lgn),对于含有n个结点的树(不是完全二叉树),最坏的情况(线性链)运行时间为Θ(n)。
二叉查找树的性质:x为二叉查找树的一个结点,x_l 为x的左子树中的一个结点,那么x_l存储的关键字小于或者等于x存储的关键字;x_r为x的右子树中的一个结点,那么x_r存储的关键字大于或者等于x存储的关键字。
如下图所示:
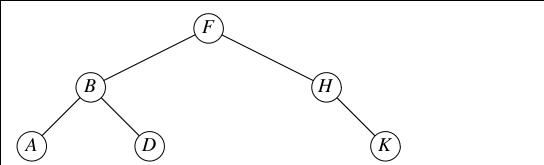
二叉树可以用链表结构来表示,每个结点除了关键字和卫星数据外,还有3个指针,分别指向左右儿子结点和父结点。
关于树结点的插入:
1、树为空;这时候要插入到树的结点为树根。
2、树不为空;从根结点开始,不断与插入结点的关键字比较,如果插入结点比较大,那么就往根结点的右子树走,否则就往左子树走;然后继续与子树的根结点比较,直到为空结点,将要插入的结点插到该位置,并将其父指针指向正确的结点。
 View Code
View Code下图为将关键字为C的结点插入到二叉查找树里:

查询也差不多,将想要查询的关键字与根结点比较(如同插入操作的第二种情况),不断的往下走,直到当前结点的关键字等于查询的关键字或者当前结点为空结点。
 View Code
View Code因为二叉查找树的特殊性质,我们很容易就可以想到关键字最小的结点的位置一定在树的最左边,关键字最大的结点一定在树的最右边。
 View Code
View Code对于结点的前趋(具有小于该结点的关键字中最大者的那个结点)、后继(具有大于该结点的关键字中最小者的那个结点)。
用后继来举例:
如果该结点存在右儿子,则后继为以其右儿子为根的子树的最小值对应的结点
如果没有右儿子,则找x结点的最低的祖先结点并且x结点处于最低祖先结点的左儿子子树里。如果在右儿子子树里,x结点的值比祖先结点的值大。
 View Code
View Code对于结点的删除,我们要确定真正删除的结点是哪一个。
因为(假设要删除的结点为z):如果z没有左右儿子,那么我们就直接用空结点代替它;如果z只有一个儿子结点,就用该结点替代它(如图a、b);以上两种情况都是删除z结点,但是当z有左右儿子结点的时候,实际上就不是删除z结点,因为如果直接删除z结点,z结点与其父结点和儿子结点的联系就失去了,树就不完整了,所以我们应该找出z结点的后继,删除它,再将它的信息替换z的信息(如图c、d)。
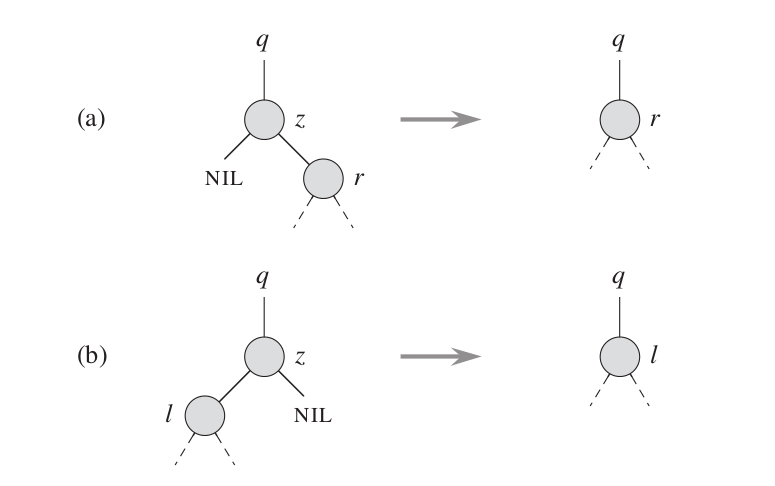

图c中z结点的后继为y结点,因为y结点没有左儿子结点,所以为z的右子树的最小值—后继。
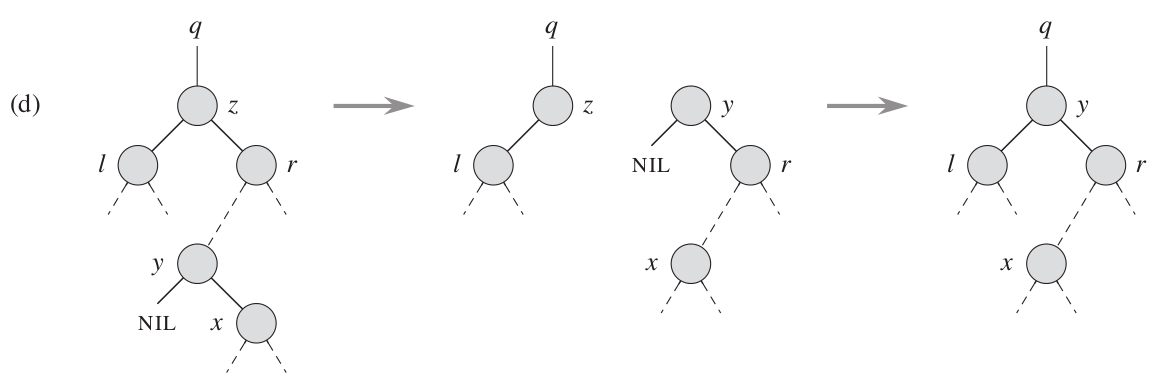
 View Code
View Code树遍历,将树中的所有关键字按特定顺序全部输出。特定顺序包括中序(关键字介于左右子树关键字之间)、前序(关键字位于左右子树关键字之前)、后序(关键字位于左右子树关键字之后)。
下列代码为原文的中序递归遍历实现:
 View Code
View Code下列为完整代码:
 View Code
View Code因为这段时间比较忙(写实验的代码、做作业、看关于Linux的书、看具体数学、突然还开始看SICP。。。晕),一直都没时间写(好烂的借口)。。。。改天会将自己觉得应该添加的完善(前序、后序,迭代版本等等)。。。
继续努力!!!!
博客能更新真的很开心!!!