快速得到栈、队列的最大值

快速得到栈、队列的最大值

特点

栈——先进后出

队列——后进先出

思路

1. 快速得到最大值的栈

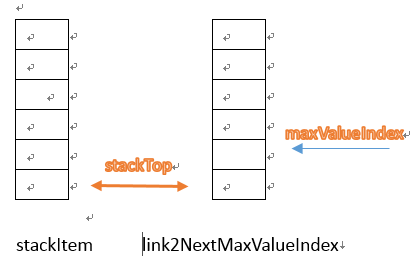
结构

1. 需要两个数组：一个数组stackItem保存栈的元素，另一个数组link2NextMaxValueIndex保存下一个最大值的位置
2. 两个指针：一个为stackTop指向栈顶，另一个为maxValueIndex指向最大值的下标

操作

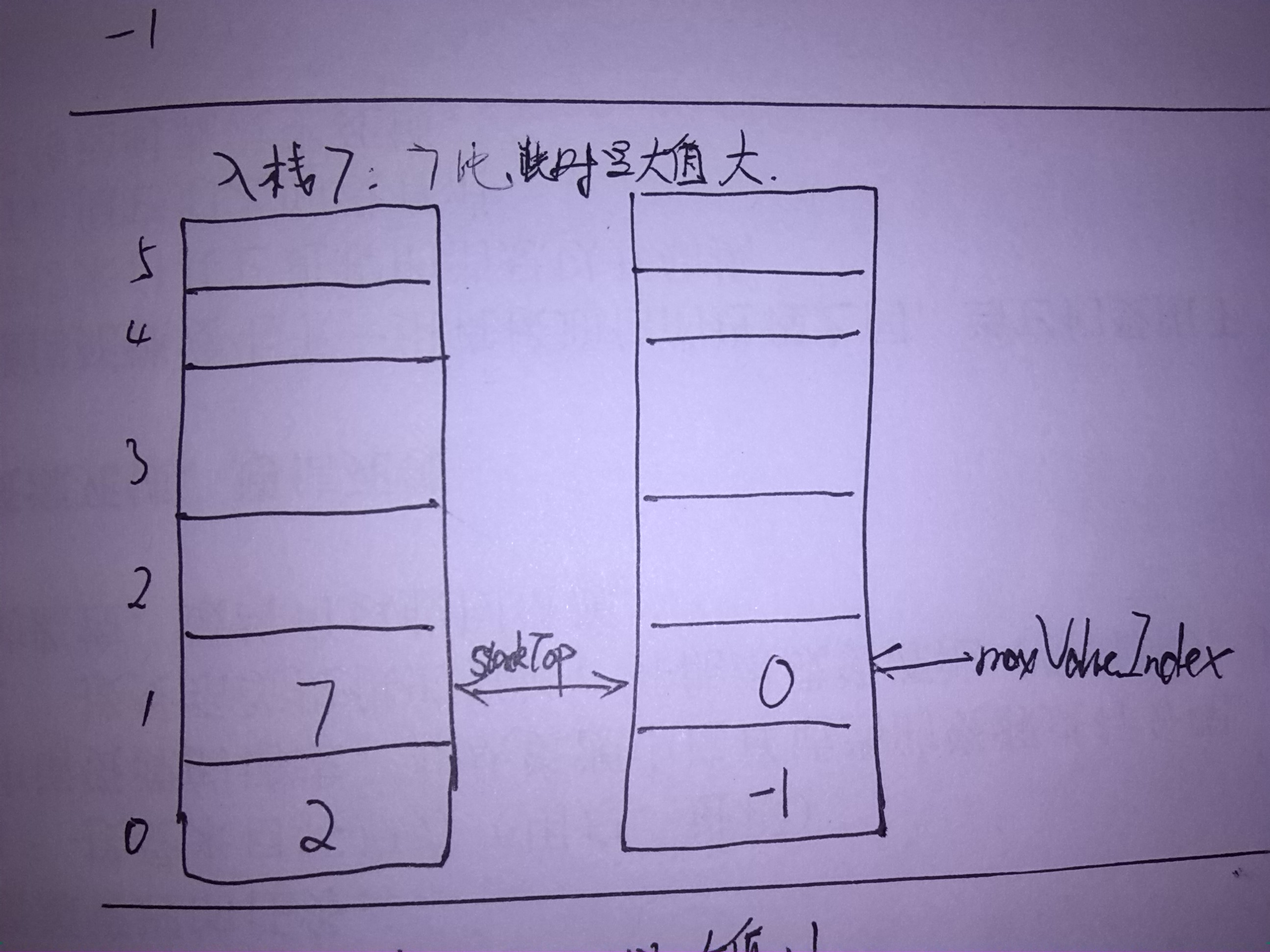
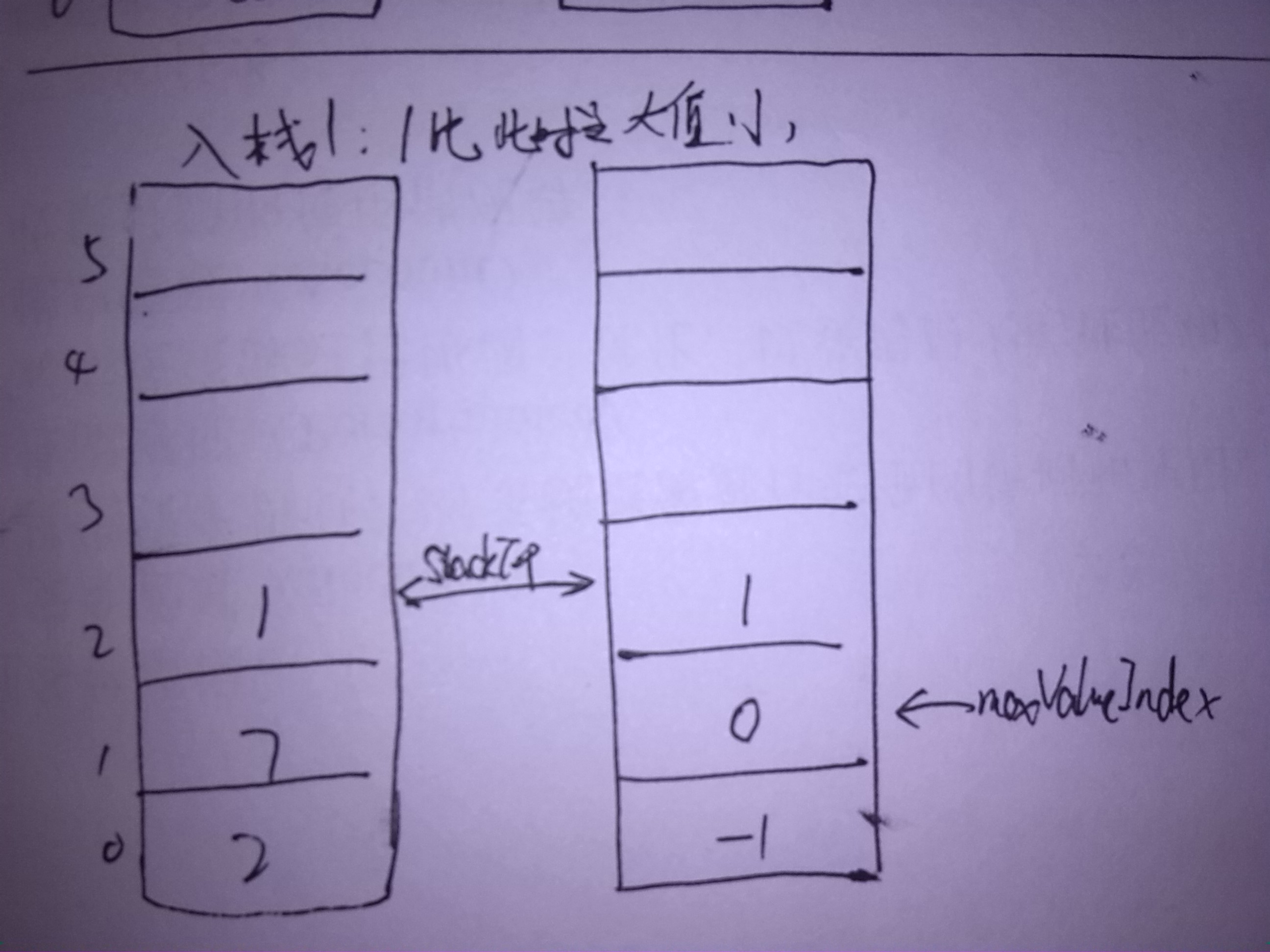
1. 插入时：比较插入元素与最大值的大小，如果比最大值还大呢，link2NextMaxValueIndex指向原来最大值的位置（即maxValueIndex），而maxValueIndex变为现在插入元素的位置；否则link2NextMaxValueIndex指向-1
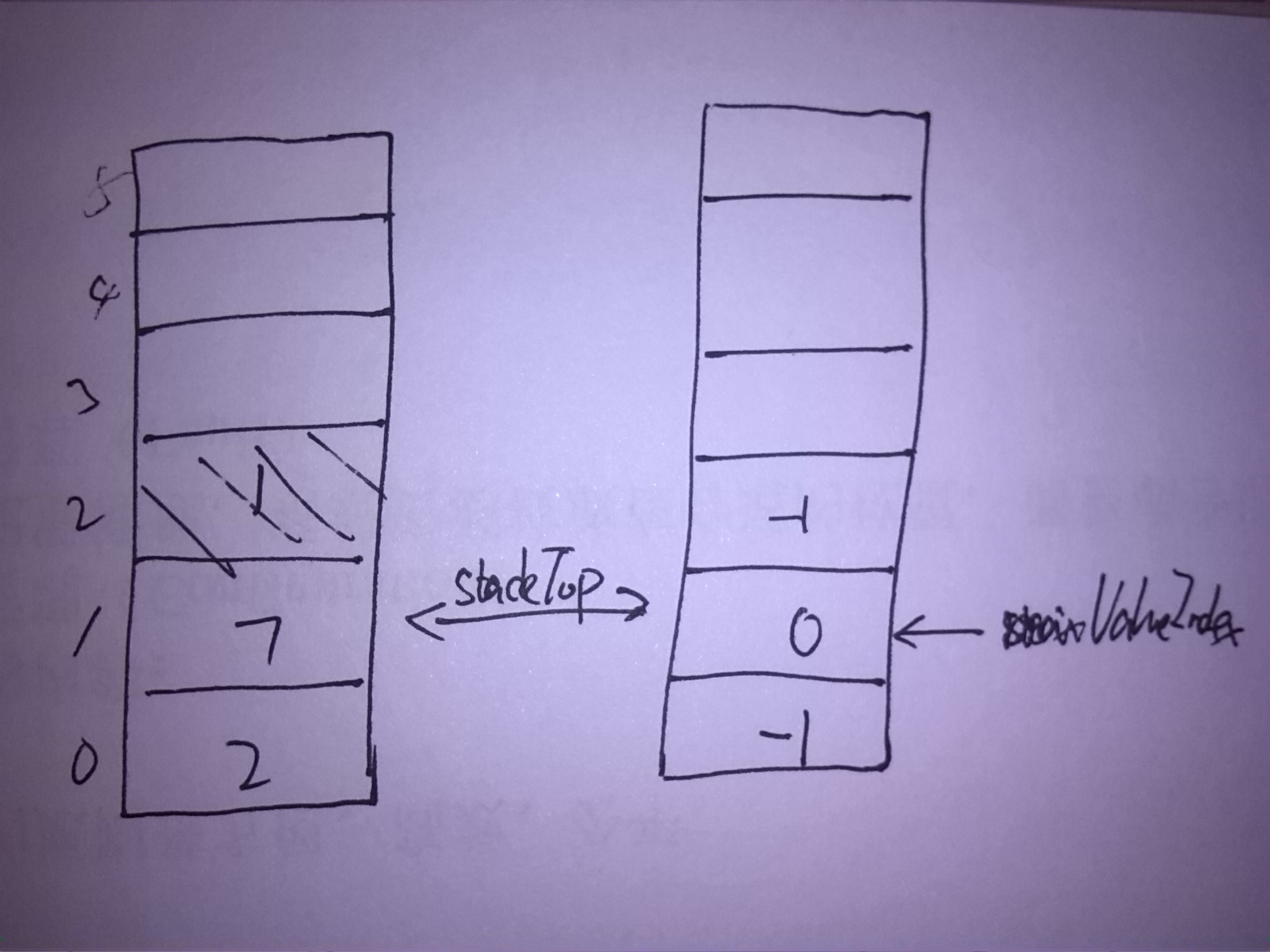
2. 删除时：删除元素的位置出，如果maxValueIndex与当前位置相同，此时maxValueIndex为link2NextMaxValueIndex[satckTop]
3. 返回栈的最大元素

图示

以入栈2 7 1，出栈为例：

 

代码

#include <iostream>
#include <climits>
#define MAX 100
using namespace std;

class stack
{
    public:
        stack() : stackTop(-1), maxValueIndex(-1) {}    
        void push(int val);
        int pop();
        int max();
        int size() { return stackTop + 1; }
        int empty() { return stackTop < 0 ? 1 : 0; }
    private:
        int stackItem[MAX];
        int link2NextMaxValueIndex[MAX];
        int stackTop;
        int maxValueIndex;
};

void stack::push(int val)
{
    ++stackTop;
    if(stackTop == MAX)
    {
        cout << "The stack has been full!" << endl;
        return;
    }
    else
    {
        stackItem[stackTop] = val;
        if(max() < val)
        {
            link2NextMaxValueIndex[stackTop] = maxValueIndex;
            maxValueIndex = stackTop;
        }
        else
            link2NextMaxValueIndex[stackTop] = -1;
    }
}
int stack::pop()
{
    int ret; 
    if(stackTop == -1)
    {
        cout << "The stack is empty!" << endl;
        return -1;
    }
    else
    {
        ret = stackItem[stackTop];
        if(stackTop == maxValueIndex)
            maxValueIndex = link2NextMaxValueIndex[stackTop];
        --stackTop;
        return ret;
    }
}
int stack::max()
{
    if(maxValueIndex >= 0)
        return stackItem[maxValueIndex];
    else
        return INT_MIN;
}


int main()
{
    stack s;
    cout << "s.empty():" << s.empty() << endl;
    s.push(3);
    s.push(4);
    cout << "s.top():" << s.pop() << endl;
    cout << "s.top():" << s.pop() << endl;
    cout << "s.top():" << s.pop() << endl;
    cout << "s.size():" << s.size() << endl;
    cout << "s.empty():" << s.empty() << endl;
}

结果

2. 快速得到最大值的队列

两个栈可以实现队列（参考），就用刚才的栈实现队列

代码

#include <iostream>
#include <climits>
#define MAX 100
using namespace std;

class stack
{
    public:
        stack() : stackTop(-1), maxValueIndex(-1) {}    
        void push(int val);
        int pop();
        int max();
        int size() { return stackTop + 1; }
        int empty() { return stackTop < 0 ? 1 : 0; }
    private:
        int stackItem[MAX];
        int link2NextMaxValueIndex[MAX];
        int stackTop;
        int maxValueIndex;
};
class queue
{
    public:
        void enQueue(int val);
        int deQueue();
        int size() { return stackIn.size() + stackOut.size(); }
    private:
        stack stackIn;
        stack stackOut;
};

void stack::push(int val)
{
    ++stackTop;
    if(stackTop == MAX)
    {
        cout << "The stack has been full!" << endl;
        return;
    }
    else
    {
        stackItem[stackTop] = val;
        if(max() < val)
        {
            link2NextMaxValueIndex[stackTop] = maxValueIndex;
            maxValueIndex = stackTop;
        }
        else
            link2NextMaxValueIndex[stackTop] = -1;
    }
}
int stack::pop()
{
    int ret; 
    if(stackTop == -1)
    {
        cout << "The stack is empty!" << endl;
        return -1;
    }
    else
    {
        ret = stackItem[stackTop];
        if(stackTop == maxValueIndex)
            maxValueIndex = link2NextMaxValueIndex[stackTop];
        --stackTop;
        return ret;
    }
}
int stack::max()
{
    if(maxValueIndex >= 0)
        return stackItem[maxValueIndex];
    else
        return -100;
}

void queue::enQueue(int val)
{
    stackIn.push(val);
}

int queue::deQueue()
{
    if(stackOut.empty() and !stackIn.empty())
    {
        while(!stackIn.empty())
            stackOut.push(stackIn.pop());
    }
    return stackOut.pop();
}

int main()
{
    stack s;
    cout << "s.empty():" << s.empty() << endl;
    s.push(3);
    s.push(4);
    cout << "s.top():" << s.pop() << endl;
    cout << "s.top():" << s.pop() << endl;
    cout << "s.top():" << s.pop() << endl;
    cout << "s.size():" << s.size() << endl;
    cout << "s.empty():" << s.empty() << endl;
    queue q;
    q.enQueue(1);
    q.enQueue(2);
    q.enQueue(3);
    cout << "q.size()" << q.size() << endl;
    q.deQueue();
    cout << "q.size()" << q.size() << endl;
}

结果

 

 

分类: 算法&&数据结构