题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3625
题意:
有n个房间,每个房间里放着一把钥匙,对应能开1到n号房间的门。
除了1号门,你可以踹开任意一扇门(不用钥匙),但你最多只能踹k次。
问你能将所有门打开的概率。
题解:
· P(打开所有门) = 能打开所有门的钥匙放置情况数 / 钥匙放置的总情况数
· 钥匙放置的总情况数 = n!
那么考虑下能打开所有门的钥匙放置情况数。。。
由于每个房间里有且只有一把钥匙,所以如果将每个房间连向房间内钥匙对应的房间,会得到一个有向图,并且由若干个独立的环组成。
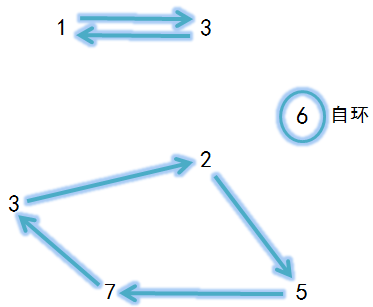
所以,只要将一个环内的任意一扇门踹开,就能打开这个环上的所有房间。
如果不考虑1号门,那么要算的就是n个元素组成1~k个环排列的情况数。
第一类Stirling数的定义啊!
递推式:s(n,k) = s(n-1,k-1) + (n-1)*s(n-1,k)
So...
· 能打开所有门的钥匙放置情况数 = ∑S(n,i) (1<=i<=k)
考虑到1号门不能踹,也就是1不能独立成环,它的情况数就等于用剩下n-1的元素组成i-1个环的情况数。
· 能打开所有门的钥匙放置情况数 = ∑( S(n,i)-S(n-1,i-1) )
所以答案为:∑( S(n,i)-S(n-1,i-1) ) / n! (1<=i<=k)
AC Code:
1 // s(n,k) = s(n-1,k-1) + (n-1)*s(n-1,k) 2 // s(n,0) = 0 s(n,n) = 1 3 // P = sigma(s[n][i]-s[n-1][i-1])/fact(n) 1<=i<=k 4 5 #include <iostream> 6 #include <stdio.h> 7 #include <string.h> 8 #define MAX_N 25 9 #define MAX_K 25 10 11 using namespace std; 12 13 int n,k,t; 14 long long sum; 15 long long s[MAX_N][MAX_K]; 16 long long fact[MAX_N]; 17 18 void stirling() 19 { 20 memset(s,0,sizeof(s)); 21 for(int i=1;i<MAX_N;i++) 22 { 23 s[i][i]=1; 24 for(int j=1;j<i;j++) 25 { 26 s[i][j]=s[i-1][j-1]+(i-1)*s[i-1][j]; 27 } 28 } 29 } 30 31 void cal_fact() 32 { 33 fact[0]=1; 34 for(int i=1;i<MAX_N;i++) 35 { 36 fact[i]=fact[i-1]*i; 37 } 38 } 39 40 int main() 41 { 42 stirling(); 43 cal_fact(); 44 cin>>t; 45 for(int cas=1;cas<=t;cas++) 46 { 47 cin>>n>>k; 48 sum=0; 49 for(int i=1;i<=k;i++) 50 { 51 sum+=s[n][i]-s[n-1][i-1]; 52 } 53 printf("%.4f ",(double)sum/fact[n]); 54 } 55 }