POJ 3744 Scout YYF I：概率dp

题目链接：http://poj.org/problem?id=3744

题意：

　　有n个地雷，位置为pos[i]。

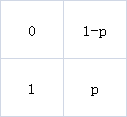
　　在每个位置，你向前走一步的概率为p，向前走两步的概率为1-p。

　　你的初始位置为1。

　　问你通过雷区的概率。

 

题解：

　　表示状态：

　　　　dp[i] = probability moving to i

　　　　表示走到i的概率

 

　　找出答案：

　　　　ans = dp[last_mine+1]

　　　　last_mine：最右边一颗雷的位置

 

　　如何转移：

　　　　dp[i] = dp[i-1] * p + dp[i-2] * (1-p)

　　　　if(i is a mine) dp[i] = 0

　　　　对于位置i，有可能是从i-1走来的，也有可能是从i-2走来的。

　　　　加法原理。

 

　　边界条件：

　　　　dp[1] = 1

　　　　初始位置为1。

 

　　优化：

　　　　矩阵快速幂。

　　　　对于某一段没有地雷的区间，是满足矩阵快速幂的（只用到递推式，dp不改为0）。

　　　　所以分段进行矩阵快速幂。

　　　　

　　　　将雷区划分为n段：

　　　　1~pos[1], pos[1]+1~pos[2], pos[2]+1~pos[3]...

　　　　

　　　　容斥原理：P（通过某一段雷区） = 1 - P（踩到最右边的雷）

　　　　乘法原理：P（通过总雷区） = ∏ P（通过每一段雷区）

 

　　　　矩阵格式：

　　　　

　　　　初始矩阵：

　　　　

　　　　特殊矩阵：

　　　　

AC Code:

// state expression:
// dp[i] = probability moving to i
//
// find the answer:
// dp[last mine + 1]
//
// transferring:
// dp[i] = dp[i-1] * p + dp[i-2] * (1-p)
//
// boundary:
// dp[1] = 1
// others = 0
//
// optimization:
// quick pow for matrix
// from x to y
// res = start * special ^ (y-x)
// dp[i] = res.val[0][0]
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define MAX_N 15
#define MAX_L 5

using namespace std;

struct Mat
{
    int n;
    int m;
    double val[MAX_L][MAX_L];
    Mat()
    {
        n=0;
        m=0;
        memset(val,0,sizeof(val));
    }
    void print_mat()
    {
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                cout<<val[i][j]<<" ";
            }
            cout<<endl;
        }
        cout<<endl;
    }
};

int n;
int pos[MAX_N];
double p;
double ans;

Mat make_unit(int k)
{
    Mat mat;
    mat.n=k;
    mat.m=k;
    for(int i=0;i<k;i++)
    {
        mat.val[i][i]=1;
    }
    return mat;
}

Mat make_start()
{
    Mat mat;
    mat.n=1;
    mat.m=2;
    mat.val[0][0]=0;
    mat.val[0][1]=1;
    return mat;
}

Mat make_special()
{
    Mat mat;
    mat.n=2;
    mat.m=2;
    mat.val[0][0]=0;
    mat.val[0][1]=1-p;
    mat.val[1][0]=1;
    mat.val[1][1]=p;
    return mat;
}

Mat mul_mat(const Mat &a,const Mat &b)
{
    Mat c;
    if(a.m!=b.n)
    {
        cout<<"Error: mul_mat"<<endl;
        return c;
    }
    c.n=a.n;
    c.m=b.m;
    for(int i=0;i<a.n;i++)
    {
        for(int j=0;j<b.m;j++)
        {
            for(int k=0;k<a.m;k++)
            {
                c.val[i][j]+=a.val[i][k]*b.val[k][j];
            }
        }
    }
    return c;
}

Mat quick_pow_mat(Mat mat,long long k)
{
    Mat ans;
    if(mat.n!=mat.m)
    {
        cout<<"Error: quick_pow_mat"<<endl;
        return ans;
    }
    ans=make_unit(mat.n);
    while(k)
    {
        if(k&1)
        {
            ans=mul_mat(ans,mat);
        }
        mat=mul_mat(mat,mat);
        k>>=1;
    }
    return ans;
}

void read()
{
    pos[0]=0;
    for(int i=1;i<=n;i++)
    {
        cin>>pos[i];
    }
}

void solve()
{
    sort(pos+1,pos+1+n);
    Mat special=make_special();
    ans=1;
    for(int i=1;i<=n;i++)
    {
        Mat start=make_start();
        Mat res=mul_mat(start,quick_pow_mat(special,pos[i]-pos[i-1]));
        ans*=(1-res.val[0][0]);
    }
}

void print()
{
    printf("%.7f
",ans);
}

int main()
{
    while(cin>>n>>p)
    {
        read();
        solve();
        print();
    }
}