Codeforces 463D Gargari and Permutations：隐式图dp【多串LCS】

题目链接：http://codeforces.com/problemset/problem/463/D

题意：

　　给你k个1到n的排列，问你它们的LCS（最长公共子序列）是多长。

 

题解：

　　因为都是1到n的排列，即每个串中，1到n每个数字恰好出现一次。

　　将相同的数字之间相连，可以得到下面的样子(n = 4, k = 3)：

　　

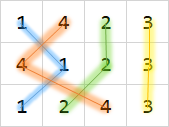
　　显然，要求的LCS就等于图中互不相交的最多连线个数。

　　将每一个数字看做一个节点。

　　若i到j有一条有向边，则代表：

　　　　数字j的连线在i的连线的后面，且互不相交。

　　即：

　　　　若i->j，则要满足所有的pos[k][i] <= pos[k][j]。

　　　　其中pos[k][i]表示第k个串中，数字i出现的位置。

　　O(N^2*K)建图，最终得到的一定是一个有向无环图。

　　LCS就等于这个图上的最长路径长度。

　　所以dfs跑一边dp就行了。

AC Code:

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
#define MAX_N 1005
#define MAX_K 10

using namespace std;

int n,k;
int dp[MAX_N];
int a[MAX_K][MAX_N];
int pos[MAX_K][MAX_N];
vector<int> edge[MAX_N];

void read()
{
    cin>>n>>k;
    for(int i=1;i<=k;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cin>>a[i][j];
            pos[i][a[i][j]]=j;
        }
    }
}

bool is_valid(int x,int y)
{
    for(int i=1;i<=k;i++)
    {
        if(pos[i][x]>=pos[i][y]) return false;
    }
    return true;
}

void build()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(is_valid(i,j)) edge[i].push_back(j);
        }
    }
}

void dfs(int now)
{
    dp[now]=1;
    for(int i=0;i<edge[now].size();i++)
    {
        int temp=edge[now][i];
        if(dp[temp]==-1) dfs(temp);
        dp[now]=max(dp[now],dp[temp]+1);
    }
}

void work()
{
    build();
    memset(dp,-1,sizeof(dp));
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(dp[i]==-1) dfs(i);
        ans=max(ans,dp[i]);
    }
    cout<<ans<<endl;
}

int main()
{
    read();
    work();
}