基于树的查找法
基于树的查找法是将待查表组织成特定树的形式并在树结构上实现查找的方法,主要包括二叉排序树、平衡二叉树和B树等。
二叉排序树
二叉排序树的定义与描述
二叉排序树又称二叉查找树,它是一种特殊的二叉树。其定义为:二叉树排序树或者是一颗空树,或者是具有如下性质的二叉树。
①若它的左子树非空,则左子树上的所有节点的值均小于根节点的值。
②若它的右子树非空,则右子树上所有节点的值均大于或等于根节点的值。
③它的左右子树也分别为二叉排序树。
二叉排序树的插入与创建
二叉排序树的插入
已知一个关键字值为key的节点s,若将其插入到二叉排序树中,只要保证插入后仍符合二叉排序树的定义即可。
①若二叉排序树是空树,则key成为二叉排序树的根。
②若二叉排序树非空,则将key与二叉排序树的根进行比较:
a、若key的值等于根节点的值,则停止插入。
b、若key的值小于根节点的值,则将key插入左子树。
c、若key的值大于根节点的值,则将key插入右子树。
可以看出二叉排序树的插入,即插入每一个节点都是作为叶子,将其插到二叉排序树的合适位置,插入时不需要移动元素,不涉及树的整体改动。
时间复杂度:$O(log_2^n)$
创建二叉排序树
首先将二叉排序树初始化为一颗空树,然后逐个读入元素,每读入一个元素,就建立一个新的结点,并插入到当前已生成的二叉排序树中,即通过多次调用二叉排序树的插入新结点的算法实现。插入时比较结点的顺序始终是从二叉排序树的根结点开始的。
假设共有n个元素插入n个结点需要n次插入操作,而一次插入操作时间复杂度为$O(log_2^n)$,
因此创建此二叉树的时间复杂度为$O(nlog_2^n)$。
注意:具有同样元素的序列,输入顺序不同,所创建的二叉树形态不同。
二叉排序树查找
因为二叉排序树可以看作是一个有序表,所以在二叉排序树上进行查找和折半查找类似。
首先将带查找关键字key与根结点关键字t进行比较,如果:
① key == t 返回根结点地址
② key < t 进一步查左子树
③ key > t 进一步查右子树
在二叉排序树中查找一个记录时,期比较次数不超过树的深度。对长度为n的有序表而言,查找的判定树是不唯一的。因为对于同一个关键字的集合,关键字插入的顺序不同,二叉树的形态也不同。所以平均查找长度(ASL)也会不同。
二叉排序树的删除
从二叉排序树中删除一个结点,不能把以该结点为根的子树都删去,只能删掉该结点,并且还要保证删除后所结点二叉树仍满足二叉排序树的性质不变。
三处操作首先要找到删除的结点,看是否在二叉排序树中,若不在则不做任何操作,否则假设要删除的结点为p,结点p的双亲结点为f,并假设结点p是结点f的左孩子(右孩子情况类似)。(分一下三种情况讨论)
① 若p为叶节点,则可以直接删除。
② 若p结点只有左子树或者右子树,可将p的左子树或右子树直接改为其双亲结点f的左子树。
③ 若p既有左子树又有右子树
a、找到p的直接前驱s,然后将p的左子树改为f的左子树,右子树改为s的右子树。
b、找到p的直接前驱s,用s结点的值替代p结点的值,再将s结点删除。将s的左子树改为s双亲结点q的右子树。
时间复杂度$O(log_2^n)$
二叉排序树的特征
中序遍历一个二叉排序树可以得到一个有序的递增序列。
平衡二叉排序树
平衡二叉树又称AVL树。一颗平衡二叉树或者是空树或者是具有下列性质的二叉排序树:
①、左子树与右子树的高度之差绝对值小于等于1(左右子树深度之差)
②、左右子树也是平衡二叉树。
平衡二叉树,其所有节点的平衡因子只能是 -1,0,1。当在一个平衡二叉树上插入一个元素时有可能出现失去平衡的情况。
失衡二叉树分类及调整方法
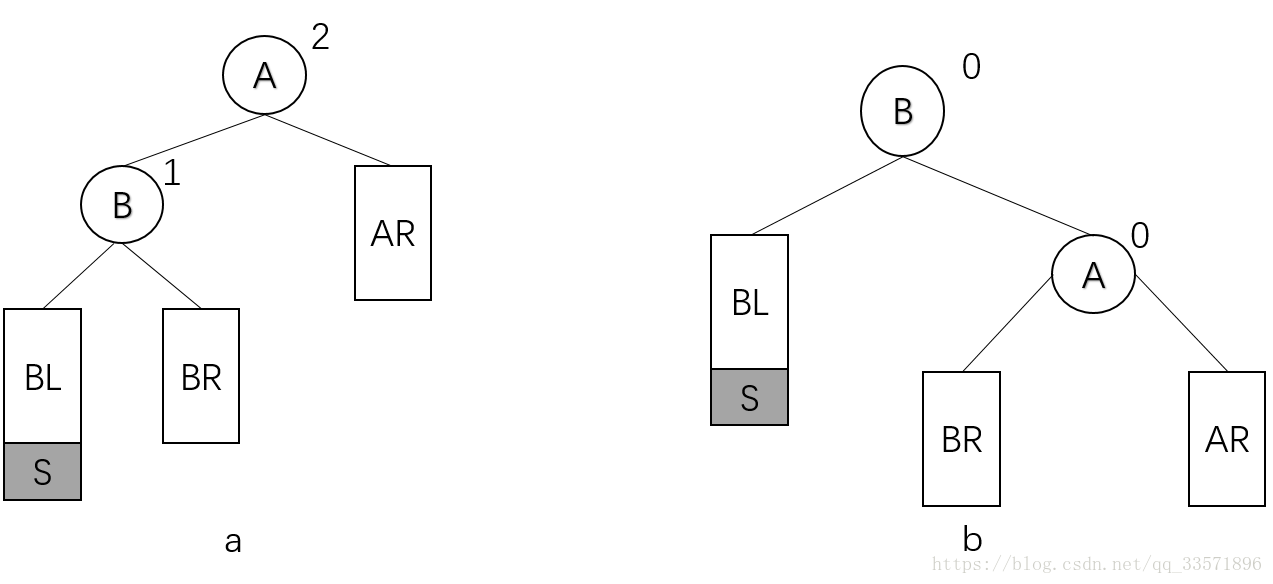
LL型
设最底层失衡结点为A,在结点A的左子树的左子树插入新的结点S后导致失衡。有A和B的平衡因子容易推知,BL,BR以及AR深度相同。为恢复平衡并保持二叉排序树特性,可将A改为B的右孩子,B原来的右孩子BR改为A的左孩子。这相当于以B为轴对A做了一次顺时针旋转。
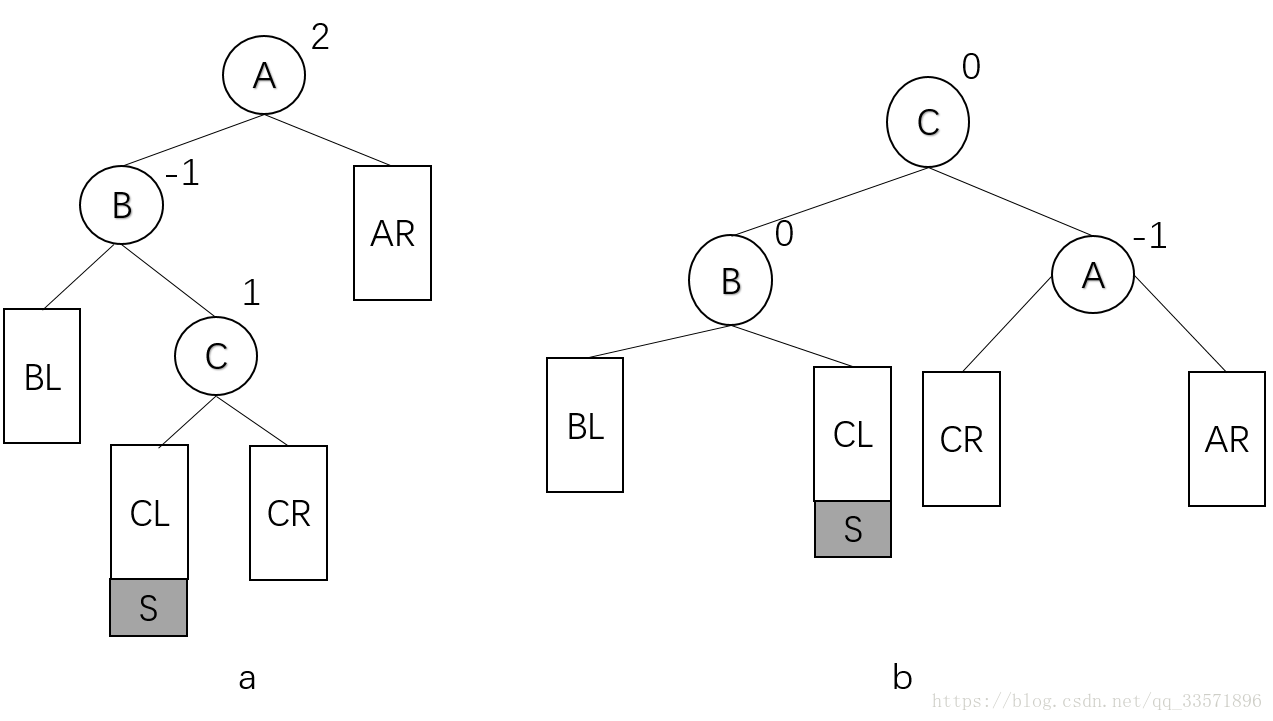
LR型
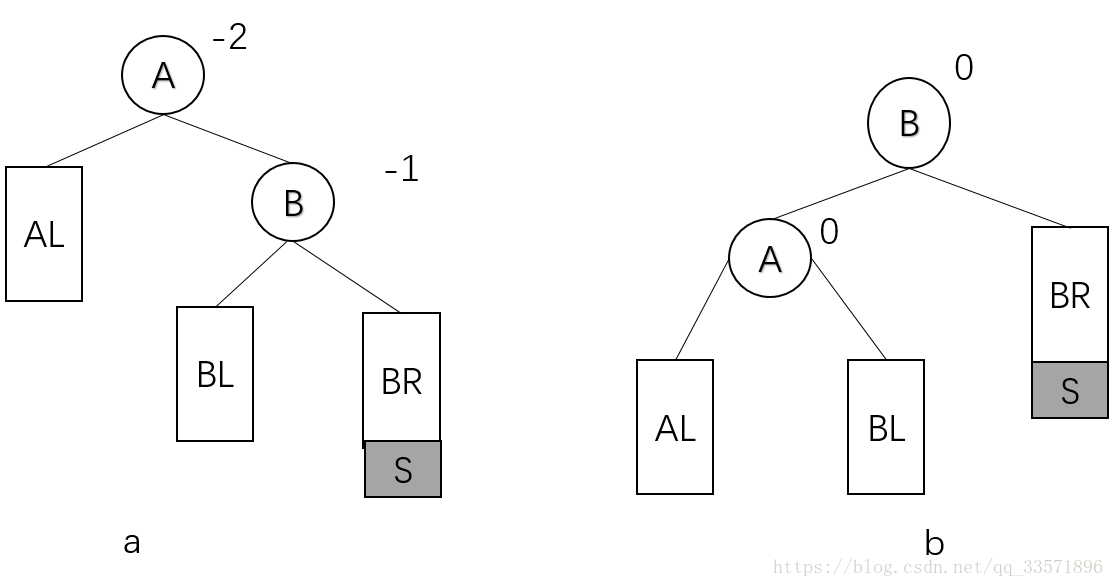
RR型
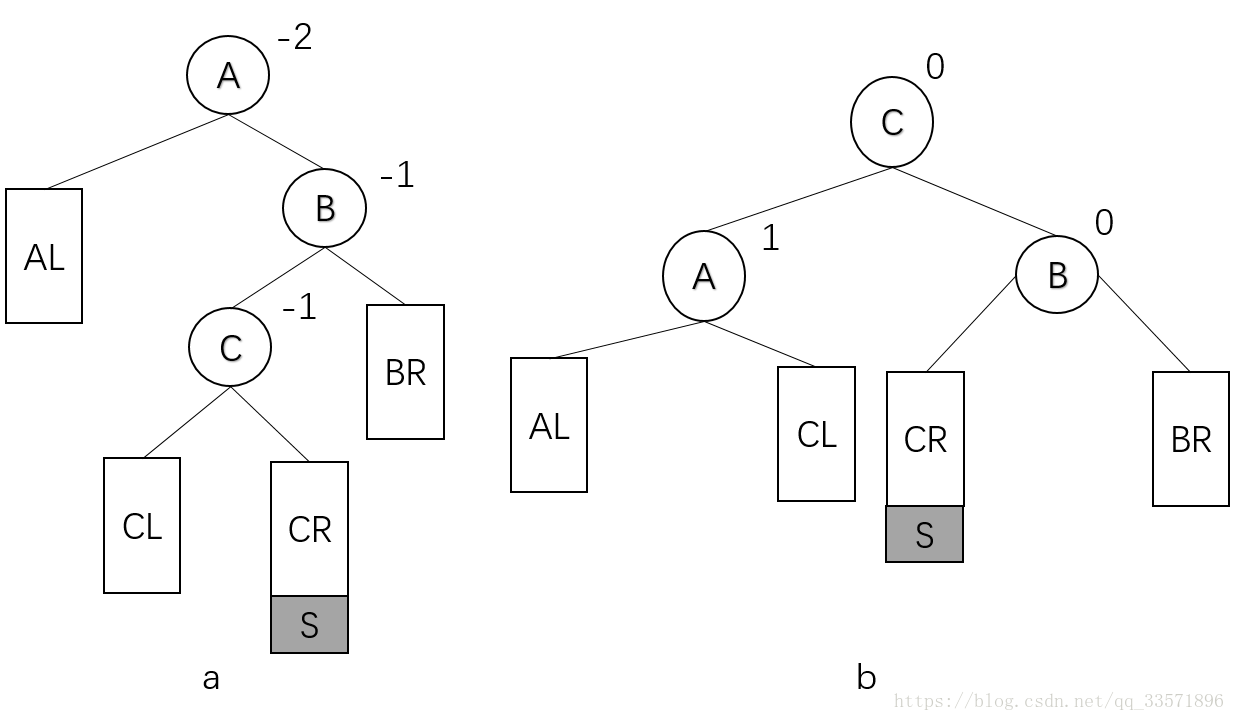
RL型
插入操作
①、查找应插入位置,同时记录下插入位置最近的可能失衡的结点A。
②、插入新的结点S。
③、确定结点B,并修改A的平衡因子。
④、修改从B到S路径上各结点的平衡因子(原值必为0,否则A下移)。
⑤、根据A,B的平衡因子,判断是否失衡以及失衡类型,并处理。
时间复杂度是$O(log_2^n)$