树的直径

树的直径定义：一棵树的直径就是这棵树上存在的最长路径。

树的直径的求法与结论：两次dfs或bfs。第一次任意选一个点进行dfs(bfs)找到离它最远的点，此点就是最长路的一个端点，再以此点进行dfs（bfs），找到离它最远的点，此点就是最长路的另一个端点，于是就找到了树的直径。

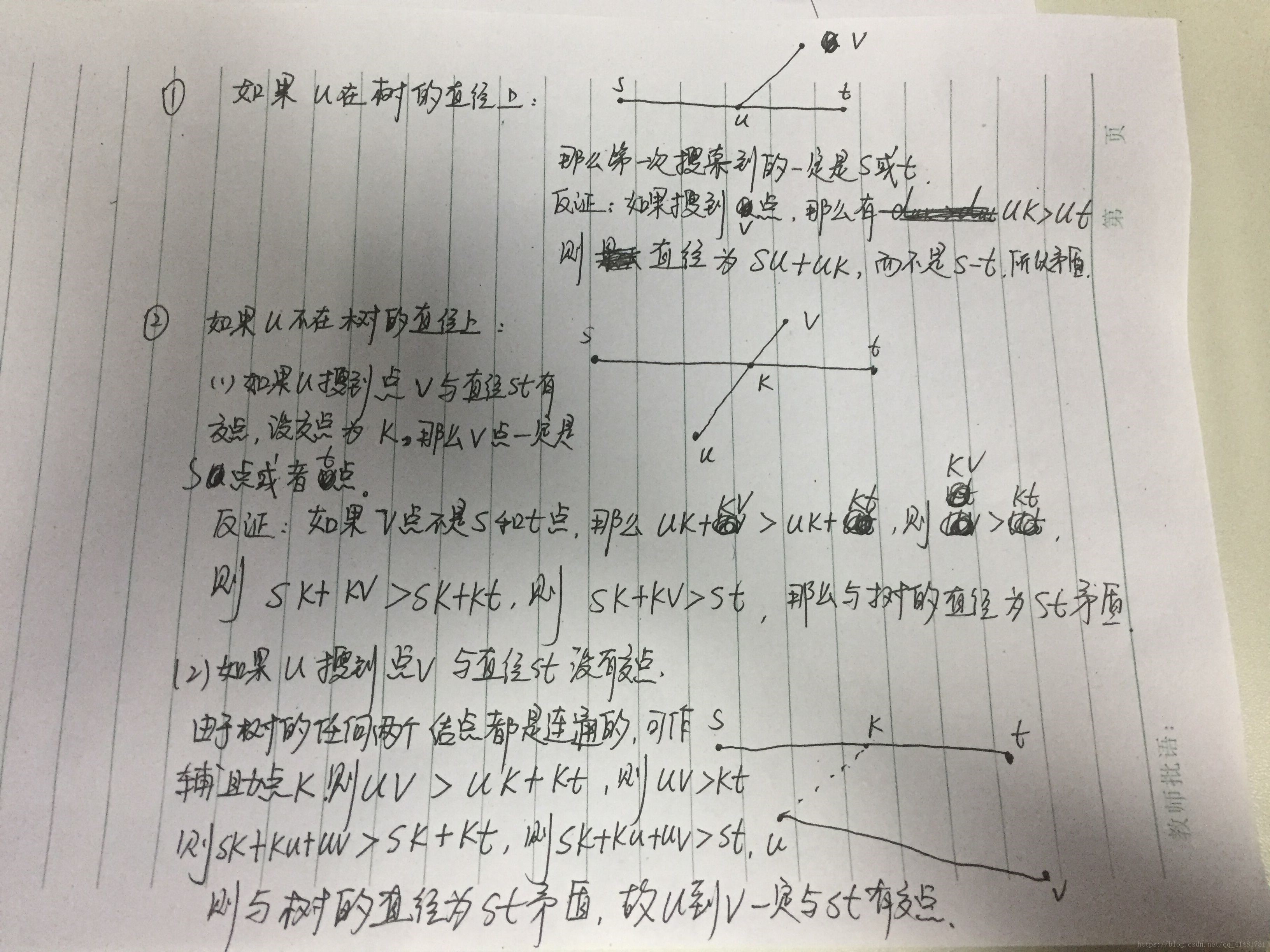
树的直径的证明：

假设此树的最长路径是从s到t,我们选择的点为u。反证法：假设搜到的点是v。
1、v在这条最长路径上，那么dis[u,v]>dis[u,v]+dis[v,s],显然矛盾。
2、v不在这条最长路径上，我们在最长路径上选择一个点为po，则dis[u,v]>dis[u,po]+dis[po,t]，那么有dis[s,v]=dis[s,po]+dis[po,u]+dis[u,v]>dis[s,po]+dis[po,t]=dis[s,t],即dis[s,v]>dis[s,t],矛盾。
也许你想说u本身就在最长路径，或则其它的一些情况，但其实都能用类似于上面的反证法来证明的。
综上所述，你两次dfs(bfs)就可以求出最长路径的两个端点和路径长度。

 树的直径的实现：

因为求树的直径题目数据量往往比较大，所以用邻接表来储存数据；至于对两个端点的查找通过bfs实现，先将第一次选择的起点a队然后开始搜索与a连接的所有边，并将权值存入dis[]数组 dis[x]=dis[top]+edge[i].w（dis[x]指的是当前搜索到的点与之前与它相 连的搜索过边的总权值，dis[top]是指当前搜索到的点的之前与它相连的搜索过边的总权值，edge[i].w是点top到当前搜索到的点 的连线的权值）完成于对当前点的搜索后，将其入队，然后对下一个点进行此操作，每次搜索时，同时将最大的权值存入sum中如此重复直至队列为空，这样这个搜素结束后，sum的值就是a点到距离其最远的点b的总权值之和；此时再以b为起点进行第二次搜索（第 二次搜 索步骤与第一次相同）

基本模板：

#include<stdio.h>
#include<string.h>
#include<queue>
#define MAX 100000
using namespace std;
int head[MAX];
int vis[MAX];//标记当前节点是否已经用过 
int dis[MAX];//记录最长距离 
int n,m,ans;
int sum;//记录最长路径的长度 
int aga;
struct node
{
    int u,v,w;
    int next;
}edge[MAX];
void add(int u,int v,int w)//向邻接表中加边 
{
    edge[ans].u=u;
    edge[ans].v=v;
    edge[ans].w=w;
    edge[ans].next=head[u];
    head[u]=ans++;
}
void getmap()
{
    int i,j;
    int a,b,c;
    ans=0;
    memset(head,-1,sizeof(head));
    while(m--)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
        add(b,a,c);
    }
}
void bfs(int beg)
{
    queue<int>q;
    memset(dis,0,sizeof(dis));
    memset(vis,0,sizeof(vis));
    int i,j;
    while(!q.empty())
        q.pop();
    aga=beg;
    sum=0;
    vis[beg]=1;
    q.push(beg);
    int top;
    while(!q.empty())
    {
        top=q.front();
        q.pop();
        for(i=head[top];i!=-1;i=edge[i].next)
        {
            if(!vis[edge[i].v])
            {
                dis[edge[i].v]=dis[top]+edge[i].w;
                vis[edge[i].v]=1;
                q.push(edge[i].v);
                if(sum<dis[edge[i].v])
                {
                    sum=dis[edge[i].v];
                    aga=edge[i].v;
                } 
            }
        }
    }
}
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        getmap();
        bfs(1);//搜索最长路径的一个端点 
        bfs(aga);//搜索另一个端点 
        printf("%d
",sum);
    }
    return 0;
}