SDUT 3364 数据结构实验之图论八：欧拉回路

数据结构实验之图论八：欧拉回路

Time Limit: 1000MS Memory Limit: 65536KB

Submit Statistic

Problem Description

在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。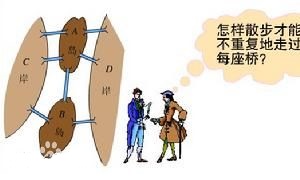



能否走过这样的七座桥，并且每桥只走一次？瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡七桥问题，并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理。对于一个连通图，通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。

你的任务是：对于给定的一组无向图数据，判断其是否成其为欧拉图？

Input

连续T组数据输入，每组数据第一行给出两个正整数，分别表示结点数目N(1 < N <= 1000)和边数M；随后M行对应M条边，每行给出两个正整数，分别表示该边连通的两个结点的编号，结点从1～N编号。 

Output

若为欧拉图输出1，否则输出0。

Example Input

1
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

Example Output

1

Hint

如果无向图连通并且所有结点的度都是偶数，则存在欧拉回路，否则不存在。 

 

DQE：

本题其实很简单不要想复杂了，注意题目Hint给的判定条件，执行一次深度优先搜索即可解决，祝大家顺利AC~

 

#include <iostream>
#include <cstdio>

using namespace std;

#define MVN 1010

typedef struct AdjMatrix
{
    int w;
    char *info;
}AM;

typedef struct MGraph
{
    int vex[MVN];
    AM arc[MVN][MVN];
    int vexnum,arcnum;
}MG;

void creat(MG &G)
{
    int i,j,k;
    for(k=1;k<=G.vexnum;k++)
        G.vex[k]=k;
    for(k=1;k<=G.arcnum;k++)
    {
        scanf("%d %d",&i,&j);
        G.arc[i][0].w++;
        G.arc[j][0].w++;
        G.arc[i][j].w=1;
        G.arc[j][i].w=1;
    }
}

int count;
void DFS(MG G,bool *visited,int i)
{
    visited[i]=true;
    count++;
    int k;
    for(k=1;k<=G.vexnum;k++)
    {
        if(G.arc[i][k].w>0&&visited[k]==false)
            DFS(G,visited,k);
    }
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        MG G={0};
        scanf("%d %d",&G.vexnum,&G.arcnum);
        creat(G);
        int k,f=0;
        for(k=1;k<=G.vexnum;k++)
        {
            if(G.arc[k][0].w%2!=0)
            {
                f=1;
                break;
            }
        }
        if(f)
        {
            printf("0
");
            continue;
        }
        count=0;
        bool visited[MVN]={false};
        DFS(G,visited,1);
        if(count!=G.vexnum)
        {
            printf("0
");
            continue;
        }
        printf("1
");
    }
    return 0;
}

/***************************************************
User name: ***
Result: Accepted
Take time: 56ms
Take Memory: 11588KB
Submit time: 2016-11-09 21:56:24
****************************************************/