
前面几节课,我们认识了线性规划的标准型,和它的各种解的概念,以及线性规划的集合特征,还有就是图解法,但是这种方法,有它的缺陷,只能求解具有两个变量的线性规划问题。
在变量多的情况下,方法就失效了。

具体使用方法,首先先找一个可行域的顶点,比如下图中的x1, 与其他的可行解进行比较,用进行寻找的筛查技巧,用自由性的判别方法,来判定是不是最优解,如是,则结束。
如果不是,那就转到下一个顶点x2,并且x2要比x1优秀,如果x2对应的目标函数值比x1对应的目标函数值大的话,那么就不能找它;而应继续找下一个更加优秀的顶点,用筛查技巧,直到没有最优解或找到最优解;也就完成了该问题的求解。
下面结合例子,来看下单纯形法的求解方法:
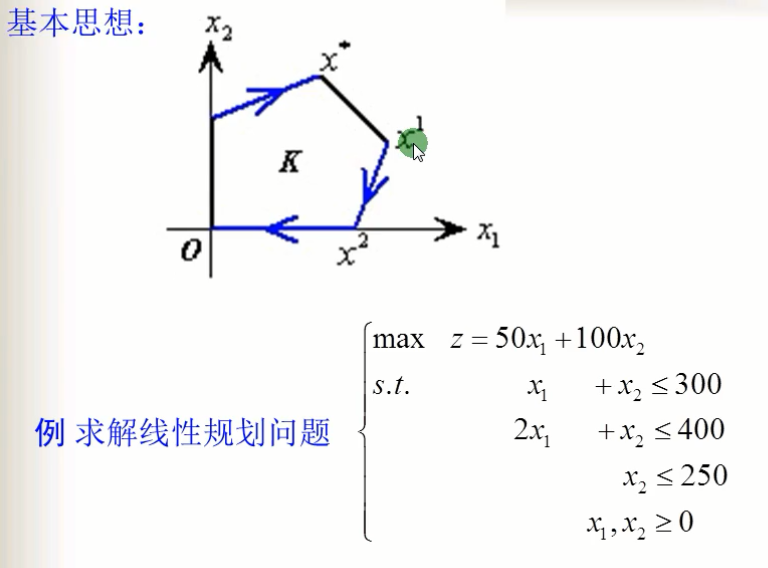
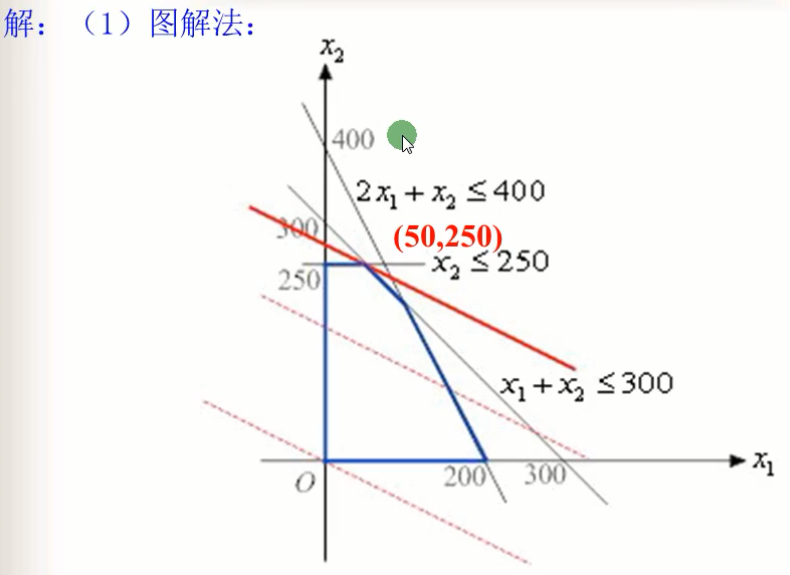
可看到法一的图形解法,找到了最优解点(50,250),下面看一下单纯形法;
