NOIP2016 D2T1 组合数问题

洛谷P2822

数学真重要啊……

其实解这一题的关键就是组合恒等式：C(n,m)=C(n-1,m)+C(n-1,m-1)，然后再知道组合数的矩阵（杨辉三角）和题中n,m的关系就很容易解决了（然而做这题之前我并不知道组合恒等式于是杯具了）

由上文提到的几何恒等式，我们可以将组合数打成如下矩阵（C(i,j)行数代表i，列数代表j（均从0开始））

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

………………

接下来我们来看要求的结论：求所有的0≤i≤n,0≤j≤min(i,m)中有多少对(i,j)使C(i,j)是k的倍数。

我乍一看到min(i,m)以为这题很复杂。但放到图中一看，想到i≥j，我们惊奇地发现，我们要求的结论就是图中共n+1行，m+1列（包括i=0,j=0）中有多少组合数是k的倍数。

画个图给大家感受一下（灵魂画手）

比如n=3,m=2，那我们就是要求图中这个部分组合数是k的倍数的数量

但询问量特别大，所以我们可以预处理一下

每访问到一个元素都枚举一个矩形很慢，但我们有递推式：d[i][j]=d[i-1][j]+d[i][j-1]-d[i-1][j-1]+!(zuhe[i][j]%k)

拿上面那个矩阵举例子

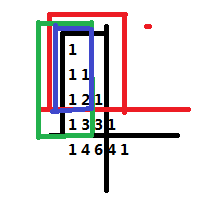
黑色部分的信息（被k整除的组合数个数）d[3][2]可以表示为红色部分的信息d[2][2]加上绿色部分的信息d[3][1]减去蓝色部分的信息d[2][1]（此信息满足区间加法和减法性质）

事实上因为c++数组自动初始化为0的问题，所以我们只会初始化有组合数部分的d值（即i≥j），那么m<n的时候怎么办呢？

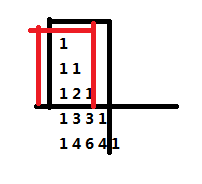
很显然图中黑色部分的信息等于红色部分的信息（因为组合数数量相等）

所以当m<n时d[m][n]=d[m][m]（在递推的时候处理或是在输出的时候处理均可，我是在输出的时候处理的）

另外此处递推的时候注意一下边界问题（i=j时），此时d[i-1][j]我们没有更新（因为i-1<j），所以此时的d[i][j]=d[i][j-1]+!(zuhe[i][j]%k)

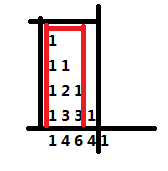
即黑色部分的信息等于红色部分的信息加上当前点的信息

还有一点小tip就是2000个组合数会很大，所以我们递推组合数的时候就将它模k，这样模k=0的组合数在表中的值就是0，上面的递推公式就改为：d[i][j]=d[i-1][j]+d[i][j-1]-d[i-1][j-1]+!zuhe[i][j](i>j),d[i][i]=d[i][i-1]+!zuhe[i][i]

剩下的就很简单了，记得初始化zuhe[1][0]=zuhe[1][1]=1即可

代码如下：

#include<cstdio>
using namespace std;
int t,k,n,m;
int zuhe[2001][2001];//存储组合数（%k意义下） 
int d[2001][2001];//存储方案个数 
int main()
{
    scanf("%d%d",&t,&k);
    zuhe[1][0]=zuhe[1][1]=1;//初始化C(1,0)=C(1,1)=1 
    for(int i=2;i<=2000;i++)
        for(int j=0;j<=i;j++)
            zuhe[i][j]=(zuhe[i-1][j]+zuhe[i-1][j-1])%k;
    for(int i=1;i<=2000;i++)
    {
        for(int j=1;j<i;j++)
            d[i][j]=d[i-1][j]+d[i][j-1]-d[i-1][j-1]+!zuhe[i][j];
        d[i][i]=d[i][i-1]+!zuhe[i][i];
    }
    while(t--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        if(n<m)
            m=n;
        printf("%d
",d[n][m]);
    }
    return 0;
}