二分图判定

概述

若一个无向图的结点可以分为不相交的两个部分使得每条边的两个端点分别在不同的部分，则称这样的无向图为二分图(bipartite graph)

算法：黑白二着色(bicoloring)

扫描所有结点，从未访问过的结点开始，将其为染色邻接点染为不同的染色。若已染色的邻接点与当前结点颜色相同，则该图不是二分图；反之该图是二分图

理解

扫描所有结点，从未访问过的结点开始

无向图不一定连通！故需要扫描所有结点进行DFS或BFS。

此外显然二分图是可合并的，任意无向图是二分图当且仅当其各个连通分量都是二分图（若均为二分图，则每个二分图的两个子集可以合并；否则无法找到两个集合满足每条边的两端点分别在两个集合）

若已染色的邻接点与当前结点颜色相同，则该图不是二分图；反之该图是二分图

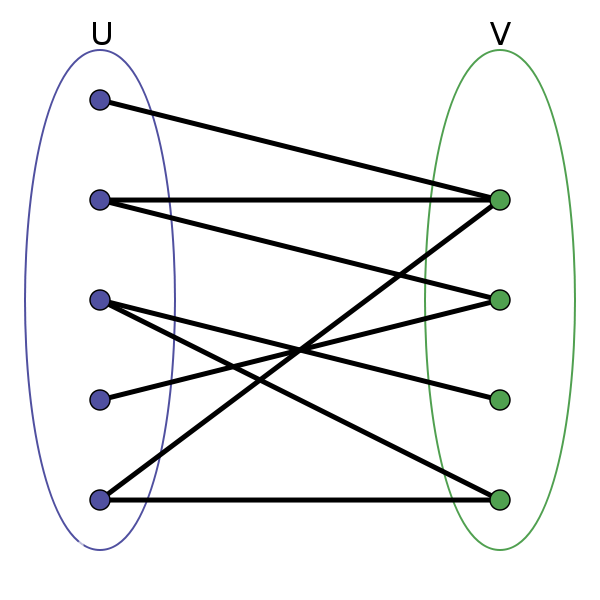
从这个图可以很清楚的看出，由二分图的定义可知，任意一个点通过一条边只能走到另一个集合中的点，一条边的两个端点的颜色一定不同。上述算法的正确性是显然的

模板

小tip：这里我把颜色定为1和2，可以用异或3代替3-

但注意选择的颜色不能和数组的初始化值相同！否则无法判定是否已被染色

DFS可能会栈溢出，所以这里给出BFS版代码

#include<cstdio>
#include<cctype>
using namespace std;
#define re register int
int read()
{
    int f=0,x=0;
    char c=getchar();
    while(!isdigit(c))
    {
        f=f|c=='-';
        c=getchar();
    }
    while(isdigit(c))
    {
        x=(x<<1)+(x<<3)+(c^48);
        c=getchar();
    }
    return x;
}
struct edge
{
    int to,pre;
}edges[1000001];
int head[1000001],tot;
int n,m;
int queue[1000001],left=1,right=0;
int color[1000001];//表示每个点的颜色（1为白，2为黑） 
bool bipartite()
{
    for(int i=1;i<=n;i++)
        if(!color[i])
        {
            queue[++right]=i;
            color[i]=1;
            while(right>=left)
            {
                int x=queue[left++];
                for(int j=head[x];j;j=edges[j].pre)
                    if(color[edges[j].to]==color[x])
                        return false;
                    else if(!color[edges[j].to])
                    {
                        color[edges[j].to]=3^color[x];
                        queue[++right]=edges[j].to;
                    }
            }
        }
    return true;
}
void add(int x,int y)//邻接表存边 
{
    edges[++tot].to=y;
    edges[tot].pre=head[x];
    head[x]=tot;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y),add(y,x);
    }
    printf("%d
",bipartite());
    return 0;
}