感知机、超平面

1.感知机
感知机是一种二分类的线性分类模型，输入为实例的特征向量，输出为实例的类别{+1，-1}。感知机要求数据集是线性可分的。
按照统计学习三要素模型、策略、算法的顺序来介绍。

2.感知机模型
由输入空间到输出空间的如下函数：
f(x)=sign(ω⋅x+b)
f(x)=sign(ω⋅x+b)

其中ω，bω，b 为模型参数，ω⊂Rnω⊂Rn叫权值（weight）或权值向量（weight vector）,b⊂Rb⊂R叫偏置。
感知机模型的假设空间是定义在特征空间中的所有线性分类模型（linear classification model）或线性分类器（linear classifier），即函数集合{f|f(x)=ω⋅x+b}{f|f(x)=ω⋅x+b}.
2.1感知机模型的几何解释
线性方程ω⋅x+bω⋅x+b对应于特征空间的一个超平面S，ωω代表超平面的法向量，bb代表截距。这个超平面将特征空间分为两个部分，位于两部分的点（特征向量）被划分为正负两类，所以超平面S被称为分离超平面（separating hyperplane）。

　　　　　　　　　　　　　　　　　　　

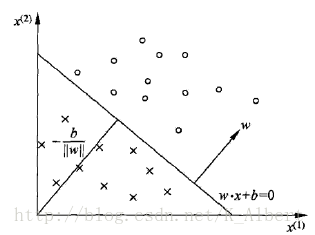
在看几何模型这里有几点疑惑：
1.超平面是什么
2.原点到超平面的距离−b∥ω∥−b‖ω‖（纯属高数忘的差不多了）

2.1.1超平面
百度百科给出的定义：超平面是n维欧式空间中余维度等于一的线性子空间（也就是说超平面的维度为n-1）。这是平面中的直线、空间中的平面之推广。

似乎并没有起到什么帮助理解的作用！这个东西为什么要叫超平面也是很迷！刨除这个蜜汁叫法，还是试图从公式上进行理解吧。

百度到资料一：给定RnRn空间中的一点pp和非零向量n⃗ n→，满足
n⃗ ⋅(x−p)=0
n→⋅(x−p)=0
的点集xx称为经过点pp的超平面。向量n⃗ n→为该超平面的法向量。按照这个定义，一条直线是R2R2空间的超平面，一个平面是R3R3空间的超平面。

老学长解惑：在RnRn空间中的超平面为：
ω⃗ T⋅x⃗ +b=0
ω→T⋅x→+b=0

在几维空间中，向量ω⃗ ,x⃗ ω→,x→就是几维的。当然，ω⃗ ，x⃗ ω→，x→属于该空间。在二维空间下，该方程表示一条直线，直线是平面的超平面。三维空间下，该方程表示一个平面，平面是空间的超平面。
老学长这个解释，我还是比较能接受的。

2.1.2点到超平面的距离
写到这里，我已决心要重看一遍高数。
向量的投影：给定两个向量u⃗ ,v⃗ u→,v→,求u⃗ u→在v⃗ v→上的投影长度，向量间的夹角为cosθcos⁡θ。

　　　　　　　　　　　　

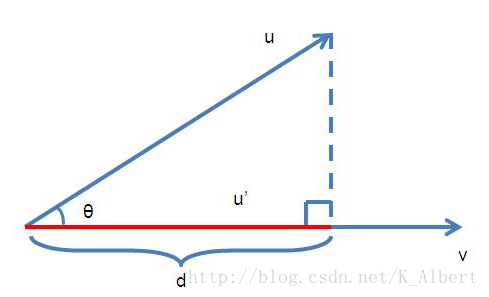
算不上推导的推导：
d=|u|⋅cosθ
d=|u|⋅cos⁡θ

cosθ=u⋅v|u||v|
cos⁡θ=u⋅v|u||v|

综上，
d=u⋅v|v|
d=u⋅v|v|

点到超平面的距离：假设x⃗ 0x→0是超平面ω⃗ T⋅x⃗ +b=0ω→T⋅x→+b=0上任意一点，则点xx到超平面的距离为x⃗ −x⃗ 0x→−x→0在超平面法向量ω⃗ ω→上的投影长度：
d=|ω⃗ T(x⃗ −x⃗ 0)|∥ω⃗ ∥=|ω⃗ T⋅x⃗ +b−ω⃗ T⋅x⃗ 0−b|∥ω⃗ ∥=|ω⃗ T⋅x+b|∥ω⃗ ∥
d=|ω→T(x→−x→0)|‖ω→‖=|ω→T⋅x→+b−ω→T⋅x→0−b|‖ω→‖=|ω→T⋅x+b|‖ω→‖
2.1.3超平面的正反面
一个超平面可以将该空间分成两部分，和法向量同向规定为正面，和法向量反向称为反面。x⃗ 0x→0是超平面上的一点，x⃗ −x⃗ 0x→−x→0与ω⃗ ω→的夹角小于90。90。时该点位于超平面正面，即
ω⃗ T⋅(x⃗ −x⃗ 0)>0
ω→T⋅(x→−x→0)>0

ω⃗ T⋅x⃗ +b>0
ω→T⋅x→+b>0
3.感知机学习策略
3.1损失函数
误分类集M，对于xi∈Mxi∈M,有−yi(ω⋅xi+b)>0−yi(ω⋅xi+b)>0，感知机损失函数与误分类点到超平面的距离有关。所有误分类点到超平面的距离和为
−1∥ω∥∑xi∈Myi(ω⋅xi+b)
−1‖ω‖∑xi∈Myi(ω⋅xi+b)

忽略1∥ω∥1‖ω‖，就得到了损失函数：
L(ω,b)=−∑xi∈Myi(ω⋅xi+b)
L(ω,b)=−∑xi∈Myi(ω⋅xi+b)
4.感知机学习算法
感知机学习问题转换为求解使损失函数L(ω,b)L(ω,b)最小的最优化问题，采用随机梯度下降法（stochastic gradient descent）。
∇ωL(ω,b)=−∑xi∈Myixi
∇ωL(ω,b)=−∑xi∈Myixi

∇bL(ω,b)=−∑xi∈Myi
∇bL(ω,b)=−∑xi∈Myi

其中M是误分类集
(1)ω=ω0,b=b0ω=ω0,b=b0，学习速率ηη
(2)选择xi∈Mxi∈M，更新ω,bω,b
ωk=ωk−1+ηyixi
ωk=ωk−1+ηyixi

bk=bk−1+ηyi
bk=bk−1+ηyi

(3)转至(2)，直到不存在误分类点。
4.1感知机学习算法的收敛性
4.1.1定理
为了便于叙述，令ω^=(ωT,b),x^=(xT,1)Tω^=(ωT,b),x^=(xT,1)T,显然ω^⋅x^=ω⋅x+bω^⋅x^=ω⋅x+b.
假设训练集是线性可分的，则
(1)存在∥ω^opt∥=1‖ω^opt‖=1的超平面，使
yi(ω^opt⋅x^i)≥γ
yi(ω^opt⋅x^i)≥γ

(2)R=max1≤i≤n∥x^i∥R=max1≤i≤n‖x^i‖,则误分类次数k满足
k≤(Rγ)2
k≤(Rγ)2
4.1.2证明
(1)由于训练数据集是线性可分的，所以存在超平面可以将训练数据集完全正确的分开。取此超平面为ω^opt⋅x^i=0,使∥ω^opt∥=1ω^opt⋅x^i=0,使‖ω^opt‖=1.对于数据集中所有的xixi都有
yi(ω^opt⋅x^i)>0
yi(ω^opt⋅x^i)>0

存在
γ=min{yi(ω^opt⋅x^i)}
γ=min{yi(ω^opt⋅x^i)}

使
yi(ω^opt⋅x^i)≥γ
yi(ω^opt⋅x^i)≥γ

(2)ω^k−1ω^k−1是第k次误分类前的权重向量，x^ix^i是使其误分类的点,则有
ω^k=ω^k−1+ηyix^i
ω^k=ω^k−1+ηyix^i

ω^k⋅ω^opt=ω^k−1ω^opt+ηyiω^optx^i≥ω^k−1ω^opt+ηγ≥ω^k−2ω^opt+2ηγ≥⋯≥ω0+kηγ
ω^k⋅ω^opt=ω^k−1ω^opt+ηyiω^optx^i≥ω^k−1ω^opt+ηγ≥ω^k−2ω^opt+2ηγ≥⋯≥ω0+kηγ

∥ω^k∥2=∥ω^k−1∥2+2ηyiω^k−1x^i+η2y2i∥x^i∥2
‖ω^k‖2=‖ω^k−1‖2+2ηyiω^k−1x^i+η2yi2‖x^i‖2

由于x^ix^i被ω^k−1ω^k−1误分类，所以yiω^k−1x^i<0,y2i=1yiω^k−1x^i<0,yi2=1,所以
∥ω^k∥2≤∥ω^k−1∥2+η2R2≤∥ω^k−2∥2+2η2R2≤⋯≤∥ω^0∥2+kη2R2
‖ω^k‖2≤‖ω^k−1‖2+η2R2≤‖ω^k−2‖2+2η2R2≤⋯≤‖ω^0‖2+kη2R2

当ω^0=0ω^0=0时，
ω^k⋅ω^opt≥kηγ
ω^k⋅ω^opt≥kηγ

∥ω^k∥≤k−−√ηR
‖ω^k‖≤kηR

kηγ≤ω^k⋅ω^opt≤∥ω^k∥⋅∥ω^opt∥⋅cosθ≤∥ω^k∥⋅∥ω^opt∥≤∥ω^k∥≤k−−√ηR
kηγ≤ω^k⋅ω^opt≤‖ω^k‖⋅‖ω^opt‖⋅cos⁡θ≤‖ω^k‖⋅‖ω^opt‖≤‖ω^k‖≤kηR

k2γ2≤kR2
k2γ2≤kR2

k≤(Rγ)2
k≤(Rγ)2

注意到初始条件为0时，迭代次数k与学习速率ηη无关。
5.感知机的对偶形式
感知机的对偶形式是初始值为0条件下的一种变形，似乎能起到减少每一次迭代的计算量的作用，有待验证。
————————————————
版权声明：本文为CSDN博主「K_Albert」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/K_Albert/article/details/78172230