Given the results of the rap battles in the order in which they were played, determine the minimum number of first rap battles that needed to take place before Bessie could order all of the robots by skill level.
The first line of the input consists of two integers, the number of robots n (2 ≤ n ≤ 100 000) and the number of rap battles m (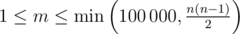 ).
).
The next m lines describe the results of the rap battles in the order they took place. Each consists of two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi), indicating that robot ui beat robot vi in the i-th rap battle. No two rap battles involve the same pair of robots.
It is guaranteed that at least one ordering of the robots satisfies all m relations.
Print the minimum k such that the ordering of the robots by skill level is uniquely defined by the first k rap battles. If there exists more than one ordering that satisfies all m relations, output -1.
4 5
2 1
1 3
2 3
4 2
4 3
4
3 2
1 2
3 2
-1
In the first sample, the robots from strongest to weakest must be (4, 2, 1, 3), which Bessie can deduce after knowing the results of the first four rap battles.
In the second sample, both (1, 3, 2) and (3, 1, 2) are possible orderings of the robots from strongest to weakest after both rap battles.
题目大意:输入第一行是n和m,代表n个点m条边,下面m行代表u为v的父亲节点,求当恰好给出多少条边时可以得到所有点的次序。
解题思路:在建树时同时记录以下这条边时给出的第几条边,用边权记录。用ans记录答案。进行拓扑排序,拓扑排序时一旦同时出现两个及以上的0入度点,则说明有多个点的次序无法准确排序,那么结果就是-1,否则向队列压入0入度点的同时记录一下ans = max(ans, 边权),整个拓扑排序结束后,这个ans就是所求结果。因为这样就相当于记录了最高次序的那个点所连接的下一个0入度点之间的边权值,也就是最多需要给出的边。
代码:
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cmath> 4 #include<cstring> 5 #include<iostream> 6 #include<algorithm> 7 #include<string> 8 #include<vector> 9 #include<queue> 10 #include<stack> 11 using namespace std; 12 const int MaxN = 1e5; 13 const int Inf = 1 << 30; 14 typedef struct 15 { 16 int to, od; 17 } Power; 18 19 vector <Power> num[MaxN+5]; 20 int n, m, ans; 21 int ind[MaxN+5]; 22 23 bool Toposort() 24 { 25 queue <int> que; 26 for(int i = 1;i <= n;i++) 27 { 28 if(ind[i] == 0) que.push(i); 29 } 30 int u; 31 Power v; 32 while(!que.empty()) 33 { 34 u = que.front(); 35 que.pop(); 36 if(!que.empty()) return 0; 37 for(int i = 0;i < num[u].size();i++) 38 { 39 v = num[u][i]; 40 ind[v.to]--; 41 if(!ind[v.to]) 42 { 43 ans = max(ans, v.od); 44 que.push(v.to); 45 } 46 } 47 } 48 return 1; 49 } 50 51 int main() 52 { 53 cin >> n >> m; 54 int a, b; 55 Power S; 56 for(int i = 1;i <= m;i++) 57 { 58 scanf("%d %d", &a, &b); 59 S.to = b;S.od = i; 60 num[a].push_back(S); 61 ind[b]++; 62 } 63 if(!Toposort()) printf("-1 "); 64 else printf("%d ", ans); 65 return 0; 66 }