Codeforces 1495F 搞了一上午的心得
不愧是div1的压轴题,真jr爽
这可比whk得劲多了!
约定
我们令题目中的 \(a_0=b_0=0\)。
\(i\) 的前驱:\(max(j:j<i,p_j>p_i)\)
\(i\) 的后继:\(min(j:j>i,p_j>p_i)\)
如果 \(i\) 不存在前驱,那么我们令 \(i\) 的前驱为 \(0\)。
注意,我们对后继并没有这个定义。
主要是后继不怎么用,后面都换成前驱了
求前驱和后继都可以用单调栈 \(O(n)\) 求所有的
题中每个点有两种方式:走到 \(i+1\),花费 \(a_i\);走到 \(i\) 的后继,花费 \(b_i\)。我们分别称它们为 \(a,b\) 转移。
题中的每个询问给定了一个点集,设这个集合是 \(S\),其中的所有点被称作 “必经点”。
思维过程
早期探索
(可以跳过)
不带修改:那还用想,单调栈求出每个点的后继,直接做就好了。 但这和正解无关
那要带上修改,咋办呢?我们发现它一下就毒瘤了起来。
慢慢来,分析性质。
我们的主观想法肯定是把 \(a\) 转移边看成一个基底,然后加上 \(b\) 转移边,考虑它的影响。
那我们反过来,把 \(b\) 转移边看成是基底,再来考虑 \(a\) 转移边。
首先我们知道所有的 \(b\) 转移边显然构成森林 (因为 \(n\) 没有后继,所以后继最多 \(n-1\) 个,所以就最多 \(n-1\) 条边,而且显然不会有环,于是构成森林)。这样再加上一些非树边。
我们发现,\(a\) 转移边在 \(b\) 转移边树上,体现出来要么是连向父亲,要么是连向兄弟 (即父亲的另一个儿子)。
往上做是不太好做的,按照树形dp的习惯,应该要往下做才是好做的。
(这时候我就去翻题解了)
标解
根据官方题解的做法,我们按照 前驱边 建一颗树,作为基底,然后把 \(a\) 和 \(b\) 都加上。注意前驱会有 \(0\),所以 \(0\) 作为树根,使整棵树连通。这里不再是森林了。
这是反常理的:正常我们会让后期加入的东西越少越好,而这里却加了一堆东西
分析性质
\(a\) 转移边相当于往儿子里走(如果是叶子就会换子树),\(b\) 转移边是直接换子树,即上面说的“连向兄弟“。
有一个显然的性质,我们要走到 \(x\),一定走过了 \(x\) 的父亲,及其上面所有点。
你可能会想,我们可能换子树过来。但是我们往前逆推,显然得先到父亲,然后到一个兄弟节点,然后才能换子树换过来 —— 无论如何,都要经过一下父亲,以及所有祖先。
还有另一个性质,如果要走到 \(x\) ,那我们还要把 \(x\) 的兄弟给走个遍。
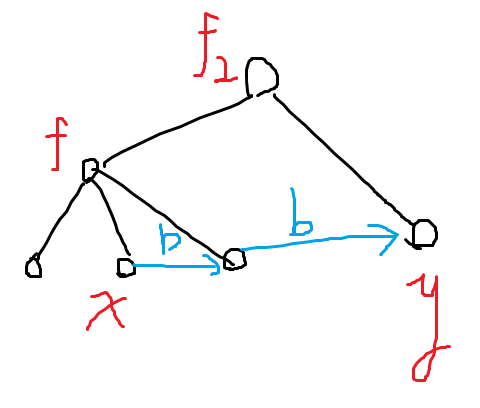
就好比这个图中,我们从 \(...f_2,f\) 一路走到了 \(x\),现在要换到 \(y\),那就要走两次 \(b\) 转移边,就要把 \(x\) 右边的兄弟走掉;
由于一次 \(a\) 转移边只能到最左边的兄弟,要找到 \(x\) 还得走一堆 \(b\) 转移,就要把 \(x\) 左边的兄弟走掉;
简单来说就是:从前面到 \(x\) 要走左兄弟,从 \(x\) 到后面要走右兄弟
于是 \(x\) 的所有兄弟都要被遍历一遍。
简化原题
由此,我们可以考虑实际要经过哪些点,是走 \(a\) 还是走 \(b\),加一下就可以了。
我们可以得到一个实际要经过的点集 \(T\),\(x\in T\) 当且仅当 \(x\) 满足下列条件之一
- \(x\) 是必经点的祖先 (包括自己),这些点要用 \(a\) 转移来走到下一个;
- \(x\) 是必经点的祖先的兄弟,这些点要用 \(b\) 转移来走到下一个。
(注意 \(0\) 也在 \(T\) 里面,并且 \(a_0=b_0=0\) )
那么我们的答案就是
然后sigma里面,\(y\not\in T\) 的条件可以先忽视,然后把 \(T\) 中所有元素的 \(b\) 都减掉。
即,我们可以令 \(c_i=a_i-b_i+\sum\limits_{j\in son(i)} b_j\)
那么答案等于 \(\sum\limits_{x\in T} c_x\)
这就完了么?还没有
有一个小细节,就是,如果一个子树里可以走一遍负的再回来(不一定回到原来的点,回到主线上去下一个点就行),那肯定要去走。它一来对大方向不影响,二来还能让答案更小。
处理树上距离前缀和的时候,更新一下就行了。
然后我们只需要每次维护一下这玩意就行了。注意要特判一下节点 \(0\)。
关于维护的细节:
设 \(Anc(x)\) 表示 \(x\) 在树上到根的链,这一个子图。
设 \(S_E(G)\) 表示图 \(G\) 的点权和。
设 \(dis(x,y)\) 表示 \(x,y\) 在树上的路径的点权和。
对于 \(x_1,x_2...x_n\),设 \(x_0=x_{n+1}=0\)
\[S_E(\bigcup\limits_{i=1}^{n} Anc(i))=\dfrac{1}{2}{\sum\limits_{i=0}^{n} dis(x_i,x_i+1)} \]左边那个到根路径的并集,其实就是本题的 \(T\)。
换句话说我们可以把 \(T\) 中所有元素 \(c\) 的和,转化成右边那个式子。
然后每次插入/删除的时候,拿 set 处理一下相邻两个的关系就行了
因为要用 set,所以复杂度带一个 \(\log\),是 \(O((n+q)\log n)\) 的。
代码
#include <bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
#define N 200005
#define int long long
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.st(u),v=G.to(i);~i;i=G.nx(i),v=G.to(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define PUT(a,n) F(i,0,n) printf("%lld ",a[i]); puts("");
int I() {char c=getchar(); int x=0; int f=1; while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar(); while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return ((f==1)?x:-x);}
template <typename T> void Rd(T& arg){arg=I();}
template <typename T,typename...Types> void Rd(T& arg,Types&...args){arg=I(); Rd(args...);}
void RA(int *p,int n) {F(i,1,n) *p=I(),++p;}
int n,q;
int p[N],a[N],b[N];
void Input()
{
Rd(n,q);
RA(p+1,n); RA(a+1,n); RA(b+1,n);
}
int st[N],top;
int fa[N],dep[N]; int jp[N][22];
int LCA(int u,int v)
{
if (dep[u]<dep[v]) swap(u,v);
D(i,20,0) if (dep[jp[u][i]]>=dep[v]) u=jp[u][i];
if (u==v) return u;
D(i,20,0) if (jp[u][i]!=jp[v][i]) u=jp[u][i],v=jp[v][i];
return fa[u];
}
int c[N]; int dis[N];
// c 就是上面说的 c
int pathlen(int u,int v) {return dis[u]+dis[v]-2ll*dis[LCA(u,v)];}
set<int> s; set<int> ::iterator it;
int cursum=0;
int vis[N]; bool visx[N];
void add(int x)
{
s.insert(x); it=s.find(x); --it;
int pre=*it;
++it; ++it;
if (it==s.end()) it=s.begin();
int nex=*it;
cursum-=pathlen(pre,nex); cursum+=pathlen(pre,x)+pathlen(x,nex);
}
void del(int x)
{
it=s.find(x); --it;
int pre=*it;
++it; ++it;
if (it==s.end()) it=s.begin();
int nex=*it;
cursum-=pathlen(pre,x)+pathlen(x,nex); cursum+=pathlen(pre,nex);
s.erase(x);
}
// 加入, 删除元素
// 用 set 维护两边关系
void Sakuya()
{
F(i,1,n)
{
while(top and p[st[top]]<p[i]) --top;
fa[i]=st[top];
st[++top]=i;
} // 单调栈求前驱
dep[0]=0; F(i,1,n) dep[i]=dep[fa[i]]+1;
// 深度
F(i,1,n) jp[i][0]=fa[i]; F(i,1,20) F(j,1,n) jp[j][i]=jp[jp[j][i-1]][i-1];
// 倍增
F(i,1,n) c[i]+=a[i]-b[i],c[fa[i]]+=b[i];
D(i,n,0)
{
dis[i]+=c[i];
if (dis[i]<0ll and i) // 下面有负的, 过去绕一圈
{
dis[fa[i]]+=dis[i];
dis[i]=0;
}
}
F(i,1,n) dis[i]+=dis[fa[i]];
vis[0]=1; s.insert(0); // 注意先搞一个 0 在这里, 不然挺麻烦的
F(i,1,q)
{
int x=I();
if (!visx[x]) // add
{
visx[x]=1;
if (!vis[fa[x]]) add(fa[x]);
++vis[fa[x]];
}
else // del
{
visx[x]=0;
if (vis[fa[x]]==1) del(fa[x]);
--vis[fa[x]];
}
printf("%lld\n",cursum/2+dis[0]);
// 特殊处理0节点
// 除以2别忘了
}
}
void IsMyWife()
{
Input();
Sakuya();
}
}
#undef int //long long
int main()
{
Flandre_Scarlet::IsMyWife();
getchar();
return 0;
}