简介
exkmp 用于求解这样的问题:
求文本串 (T) 的每一个后缀与模式串 (M) 的匹配长度(即最长公共前缀长度)。特别的,取 (M=T),得到的这个长度被称为 (Z) 函数。“函数”只是一个叫法,它本质上是个数组...为了好听,后面叫他“(Z) 数组” (互联网上的确有人这么叫)
符号(字符串)
(|S|) 表示 (S) 的长度
(S[l:r]) 表示 (S) 从 (l) 到 (r) 的子串。如果 (l) 空着,默认为 (1);同理 (r) 默认为 (|S|)。
也就是 (S[:x]) 表示 (S) 到 (x) 结束的前缀,(S[x:]) 表示 (S) 从 (x) 开始的后缀。
(LCP(S_1,S_2)) 表示 (S_1,S_2) 的 最长公共前缀 (Longest Common Prefix)
算法讲解
设 (p_i=LCP(T_i,M))
定义从 (l) 开始的匹配区间为 ([l,l+p_l-1]) (设 (l+p_l-1=r))
我们枚举处理。假设现在已经求好了 ([1,i-1]) 的 (p) 数组,要求 (p_i)。记录一个 最靠后 的匹配区间 ([l,r]) ((l<i),以 (r) 靠后为第一关键字,(l) 靠后为第二关键字),考虑直接从 ([l,r]) 中继承点答案来,那很显然一个前提就是 (ile r) (你 (i) 在 (r) 外面继承啥)
显然,(p_ige LCP(T[i:r],M)) (因为 (T[i:r]) 是 (T[i:]) 前缀)
由定义, ([l,r]) 是最长匹配长度,可知 (T[l:r]=M[1:r-l+1])。
然后现在假如 (l<ile r),那么显然 (T[i:r]=M[i-l+1:r-l+1])
那么 (LCP(T[i:r],M)=LCP(M[i-l+1:r-l+1],M))
简单想一下,(LCP(A[l:r],A)=min(LCP(A[l:],A),r-l+1))
我们要求 ([l,r]) 子串与整个串的 (LCP),可以先求以 (l) 开头的整个后缀的与整个串的 (LCP),然后和区间长度取 (min)。这显然正确。
然后有:
(LCP(M[i-l+1:r-l+1],M)=min(LCP(M[i-l+1:],M),(r-l+1)-(i-l+1+1)))
右边的 (-l+1) 两个抵消了,就变成 (r-i+1)
然后前面是 (LCP(M[i-l+1:],M)) 。这不就是 (M) 的 (Z) 数组的第 (i-l+1) 个位置吗!(还记得 (Z) 数组的定义吗?)
觉得看字母理解不了的看图(自己画的)(纯鼠标):
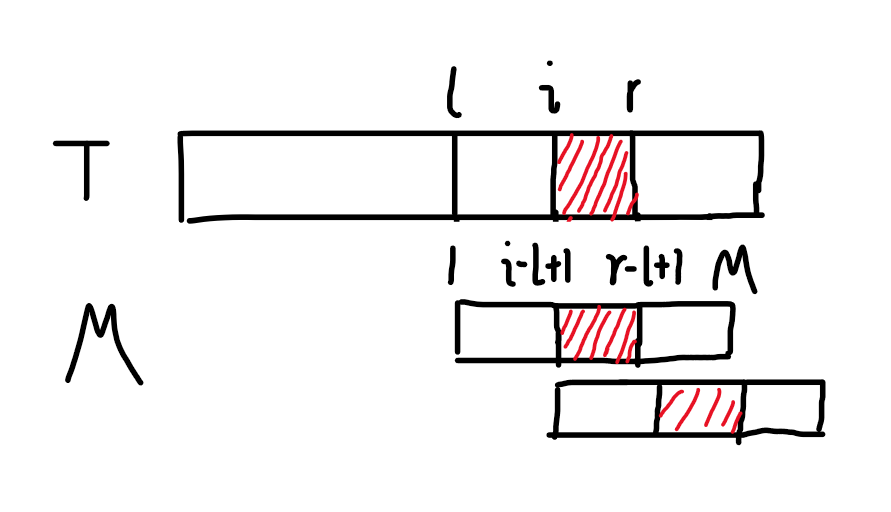
2021.05.04: 我当时还没数位板qaq
红色的部分就是我们推出来的匹配部分。然后现在我们把 (M) 移到 (i) 开头的位置来匹配,就相当于把 (M[i-l+1:r-l+1]) 这一段(红色)移到 (M) 的开头处匹配。这一段匹配的长度就是 (min(Z_{i-l+1},r-i+1))。
假设我们现在能求这个 (Z) 数组,那么我们已经知道 (p_i) 的最小值了 ,就是 (min(Z_{i-l+1},r-i+1)) 。从这个位置开始暴力即可。这样就不用每次从 (1) 开始匹配了。
求完 (p_i) 之后,记得用 ([i,i+p_i-1]) 更新 ([l,r])。
时间是线性的,我不会证,可以参考网上的证明。
如何求 Z 数组
我们发现 (Z) 数组就是自己和自己匹配的过程。然后我们把上面过程中 (M) 换成 (T) 即可。
所以我们还是记录一个最靠后的匹配区间 ([l,r]),然后 (p_i) 就相当于 (Z_i) 了。
易得:
(Z_i=min(LCP(M[i-l+1:],M),r-i+1)=min(LCP(T[i-l+1:],T),r-i+1)=min(Z_{i-l+1},r-i+1))
求完 (Z_i) 之后,记得用 ([i,i+Z_i-1]) 来更新 ([l,r])。
一样,也是从这里开始暴力即可。时间复杂度依然是线性的,可以参考网上的证明。
模板
#include <bits/stdc++.h>
using namespace std;
#define N 20000007
#define F(i,l,r) for(int i=l;i<=r;++i)
#define D(i,r,l) for(int i=r;i>=l;--i)
#define Fs(i,l,r,c) for(int i=l;i<=r;c)
#define Ds(i,r,l,c) for(int i=r;i>=l;c)
#define MEM(x,a) memset(x,a,sizeof(x))
#define FK(x) MEM(x,0)
#define Tra(i,u) for(int i=G.Start(u),v=G.To(i);~i;i=G.Next(i),v=G.To(i))
#define p_b push_back
#define sz(a) ((int)a.size())
#define all(a) a.begin(),a.end()
#define iter(a,p) (a.begin()+p)
#define Flandre_Scarlet int
#define IsMyWife main
char _c;
int I()
{
int x=0; int f=1;
while(_c<'0' or _c>'9') f=(_c=='-')?-1:1,_c=getchar();
while(_c>='0' and _c<='9') x=(x<<1)+(x<<3)+(_c^48),_c=getchar();
return (x=(f==1)?x:-x);
}
void Rd(int cnt,...)
{
va_list args; va_start(args,cnt);
F(i,1,cnt) {int* x=va_arg(args,int*);(*x)=I();}
va_end(args);
}
char a[N],b[N];
void Input()
{
scanf("%s%s",a+1,b+1);
}
int z[N];
void Z(char s[]) // 求 Z 函数
{
int n=strlen(s+1);
z[1]=n; F(i,2,n) z[i]=0;
// Z[1]=n 特判,同时也是递推边界
int l=0,r=0;
F(i,2,n)
{
if (i<=r) z[i]=min(z[i-l+1],r-i+1); // 推理出下界
while(i+z[i]<=n and s[i+z[i]]==s[z[i]+1]) ++z[i]; // 暴力
if (i+z[i]-1>=r) l=i,r=i+z[i]-1; // 更新最靠后的匹配位置
}
}
int p[N];
void ExKmp(char s[],char t[])
{
int n=strlen(s+1);
Z(t);
int l=0,r=0;
F(i,1,n)
{
if (i<=r) p[i]=min(z[i-l+1],r-i+1); // 推理出下界
while(i+p[i]<=n and s[i+p[i]]==t[p[i]+1]) ++p[i]; // 暴力
if (i+p[i]-1>r) l=i,r=i+p[i]-1; // 更新最靠后的匹配位置
}
}
void Soviet()
{
ExKmp(a,b);
int n=strlen(a+1),m=strlen(b+1);
long long ans=0;
F(i,1,m) ans^=1ll*i*(z[i]+1);
printf("%lld
",ans);
ans=0;
F(i,1,n) ans^=1ll*i*(p[i]+1);
printf("%lld
",ans);
}
Flandre_Scarlet IsMyWife()
{
Input();
Soviet();
getchar();
return 0;
}