A. 食物链
题目描述
如图所示为某生态系统的食物网示意图,据图回答此题。
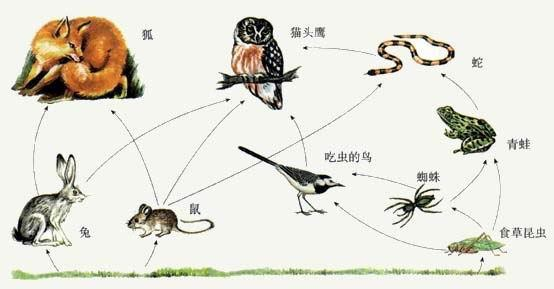
现在给你n 个物种和 m条能量流动关系,求其中的食物链条数。
物种的名称为从1 到 n的编号。
m条能量流动关系形如

其中 ai,bi表示能量从物种ai 流向物种bi 。注意单独的一种孤立生物不算一条食物链。
输入格式
第一行两个整数n 和m ,接下来 m行每行两个整数 ai,bi 描述m 条能量流动关系。
(保证输入数据符合生物学特点,即不存在环,且不会有重复的能量流动关系出现)
输出格式
一个整数,即食物网中的食物链条数。
样例
样例输入
10 16
1 2
1 4
1 10
2 3
2 5
4 3
4 5
4 8
6 5
7 6
7 9
8 5
9 8
10 6
10 7
10 9
样例输出
9
数据范围与提示

分析
此题就是一道简单的dfs,食物链(欺负学地理的,哼)从最低端到最顶端,最低端一定是入度为零的点,最顶端一定是出度为零的点,那么我们只需要统计从每一个低端(入度为零)到每一个顶端(出度为零)的点的有多少不同的路径。
Code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6;
int n,m;
int x,y;
int rd[N],cd[N];
int dp[N],head[N],cnt;
struct edge{
int to;
int ne;
}e[N];
void add(int u,int v){//建边
e[++cnt].to = v;
e[cnt].ne = head[u];
head[u] = cnt;
}
int dfs(int u){//深搜
if(dp[u])return dp[u];//记忆化搜索
int ans = 0;
if(!cd[u]&&rd[u])ans++;
for(int i = head[u];i;i = e[i].ne){//遍历
int v = e[i].to;
ans+=dfs(v);
}
dp[u]=ans;
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
add(x,y);
rd[y]++;//记录入度出度
cd[x]++;
}
int ans = 0;
for(int i = 1;i<=n;i++){
if(!rd[i])ans+=dfs(i);//对每一个入度为零的点进行深搜
}
printf("%d",ans);
return 0;
}
在贴上我的70分(TLE)代码
#include<bits/stdc++.h> using namespace std; const int N = 2e6; int n,m; int x,y; int rd[N],cd[N]; int rdd[N],cdd[N],r,c; int sum; int head[N],cnt; queue<int>q; struct edge{ int to; int ne; }e[N]; void add(int u,int v){ e[++cnt].to = v; e[cnt].ne = head[u]; head[u] = cnt; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ scanf("%d%d",&x,&y); add(x,y); rd[y]++; cd[x]++; } for(int i=1;i<=n;i++){ if(rd[i]==0&&cd[i]==0)continue; if(rd[i]==0){ rdd[++r]=i; } if(cd[i]==0){ cdd[++c]=i; } } //q.push(1); //r = 0; //printf("%d",rdd[1]); for(int i=1;i<=r;i++){ q.push(rdd[i]); //printf("%d",q.front()); while(!q.empty()){ int f = q.front(); //printf("%d",f); q.pop(); for(int j=head[f];j;j=e[j].ne){ int v = e[j].to; //printf("%d ",v); if(cd[v]==0){ sum++; continue; } q.push(v); } } } printf("%d ",sum); return 0; }
B. 升降梯上
题目描述

输入格式

输出格式

样例
样例输入
6 3 -1 0 2
样例输出
19
数据范围与提示

分析
这可以建图来解,把每次扳动看成路径,跑一边spfa
Code
#include<bits/stdc++.h> using namespace std; const int N = 4000000; int n,m; int c[N]; int num[1010][25]; int cnt; int sta; bool vis[N]; int head[N],dis[N]; queue<int>q; struct edge{ int to; int ne; int w; }e[N]; void add(int u,int v,int w){ e[++cnt].to = v; e[cnt].w = w; e[cnt].ne = head[u]; head[u] = cnt; } void spfa(int s){ memset(dis,0x7f,sizeof(dis)); q.push(s); dis[s] = 0; vis[s] = 1; while(!q.empty()){ int f = q.front(); q.pop(); vis[f] = 0; for(int i = head[f];i;i=e[i].ne){ int v = e[i].to; if(dis[v]>dis[f]+e[i].w){ dis[v]=dis[f]+e[i].w; if(!vis[v]){ q.push(v); vis[v] = 1; } } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;i++)scanf("%d",&c[i]); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ num[i][j]=++cnt; if(i==1&&c[j]==0)sta = cnt; } //cnt = 0; } for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ for(int k=1;k<=m;k++){ if(j!=k){ add(num[i][j],num[i][k],abs(j-k)); } } } } for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(c[j]!=0&&i+c[j]>=1&&i+c[j]<=n){ add(num[i][j],num[i+c[j]][j],abs(c[j]*2)); } } } //printf("%d"); spfa(sta); int ans = 2e9; for(int i=1;i<=m;i++){ ans = min(ans , dis[num[n][i]]); } if(ans>=2e9)printf("-1"); else printf("%d ",ans); return 0; }
C. Password
题目描述

输入格式

输出格式

样例
样例输入1
2 7
4 5
4 6
样例输出1
3 1
样例输入2
4 7 2 4 7 1 6 5 9 3
样例输出2
3
0
1
1分析
这是一道腻歪人的数论题~~~恶恶恶~~~烦死了数论应该多烦烦数奥的,离我远点
这种玩意我也讲不清(我也没懂呢)那就贴上学长博客
Code
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #define ll long long using namespace std; const int sj=1000010; int m; ll n,p,q,temp,k,phi[sj],s[sj],ge; bool v[sj]; void prime(ll x) { for(ll i=2;i<x;i++) { if(!v[i]) { s[ge++]=i; phi[i]=i-1; } for(ll j=0;j<ge&&i*s[j]<x;j++) { ll mb=i*s[j]; v[mb]=1; if(i%s[j]==0) { phi[mb]=phi[i]*s[j]; break; } else phi[mb]=phi[i]*(s[j]-1); } } phi[1]=1; } ll fb(ll x,ll y) { ll a[2][2]={0},ans[2][2]={0},f[2][2]={0}; a[0][0]=a[0][1]=a[1][0]=ans[1][1]=ans[0][0]=1; while(x) { if(x&1) { memset(f,0,sizeof(f)); for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int l=0;l<2;l++) f[i][j]+=ans[i][l]*a[l][j]%y; memcpy(ans,f,sizeof(f)); } x>>=1; memset(f,0,sizeof(f)); for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int l=0;l<2;l++) f[i][j]+=a[i][l]*a[l][j]%y; memcpy(f,a,sizeof(a)); } memset(f,0,sizeof(f)); memset(a,0,sizeof(a)); f[0][0]=1; f[1][0]=1; for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int l=0;l<2;l++) a[i][j]+=f[i][l]*ans[l][j]%y; return a[0][0]%y; } ll ph(ll x) { if(x<sj) return phi[x]; ll temp=x; for(ll i=2;i*i<=x;i++) if(x%i==0) { temp=temp-temp/i; while(x%i==0) x/=i; } if(x>1) temp=temp-temp/x; return temp; } ll ksm(ll x,ll y,ll z) { x%=z; ll jg=1; while(y) { if(y&1) jg=jg*x%z; x=x*x%z; y>>=1; } return jg%z; } int main() { prime(sj-1); scanf("%d%lld",&m,&p); for(int i=1;i<=m;i++) { scanf("%lld%lld",&n,&q); printf("%lld ",ksm(p,fb((n-1),ph(q)),q)); } return 0; } password
D. 子串
题目描述

输入格式

输出格式

样例
样例输入 1
6 3 1 aabaab aab
样例输出 1
2
样例输入 2
6 3 2
aabaab
aab
样例输出 2
7
样例输入 3
6 3 3 aabaab aab
样例输出 3
7
数据范围与提示
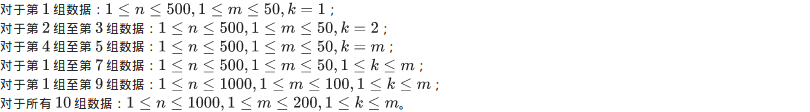
分析
dp,



Code
#include<bits/stdc++.h> const int N=1010; const int mod=1000000007; int f[2][210][210][2]; char a[N],b[210]; int n,m,k;bool val=1; void dp(){ f[0][0][0][0]=f[1][0][0][0]=1; for(int i=1;i<=n;i++,val^=1) for(int j=1;j<=m;j++) for(int p=1;p<=k;p++){ if(a[i]==b[j]){ f[val][j][p][0]=(f[val^1][j][p][0]+f[val^1][j][p][1])%mod; f[val][j][p][1]=(f[val^1][j-1][p][1]+ (f[val^1][j-1][p-1][0]+f[val^1][j-1][p-1][1])%mod)%mod; } else{ f[val][j][p][0]=(f[val^1][j][p][0]+f[val^1][j][p][1])%mod; f[val][j][p][1]=0; } } } int main(){ scanf("%d%d%d",&n,&m,&k); scanf("%s%s",a+1,b+1); dp(); printf("%d ",(f[n&1][m][k][0]+f[n&1][m][k][1])%mod); return 0; }