在本文中,我们用 $ binom{n}{m}$ 而非 $C_n^m$ 来表示从 $n$ 个互不相同的数中选出 $m$ 个(也即组合数)的方案数。
卡特兰数是组合数学中的一个常用数列,在数数题中数见不鲜(注意它与卡特兰常数,也即卡常数的区别),我们用 $C_n$ 来表示卡特兰数的第 $n$ 项。其下标从 $0$ 开始,前几项依次为 $1,1,2,5,14,42,132,...$ (这有助于我们通过找寻规律来解决良心出题人精心出的高质量好题)。
要研究一个数列,首先就得知道它的意义。但卡特兰数的意义非常广泛,所以这里只举出两个最典型的例子来阐述它的意义。
第一个例子是折线问题:在平面直角坐标系中,你在 $(0,0)$ ,目的地在 $(n,n)$ ,每次你可以选择向右走一步或向上走一步,但你不能穿过直线 $y=x$ (但可以走到直线上面)。你有着充分多的闲暇时间,于是便想把所有不同的走法都试一遍(两种走法不同当且仅当存在一个点在其中一种走法中被走到过而在另一种走法中未被走到),那么问题来了,不同的走法一共有几种呢?

事实上这个问题的解可以作为卡特兰数的一个定义,我们可以定义 $C_n$ 为折线问题中从 $(0,0)$ 走到 $(n,n)$ 的方案数。
对于一个数列,我们一定很想得到它的递推式与通项式。我们先研究一下它的递推式。考虑枚举它在到达 $(n,n)$ 前走到的最后一个 $y=x$ 上的点,设其为 $(i,i)(0le ile n-1)$ 。那么,到达这个点前可以按照规则随便走,方案数为 $C_i$ ,到达这个点后不能碰到直线 $y=x$ ,相当于第一步向右,最后一步向上,从 $(i+1,i)$ 走到 $(n,n-1)$ ,中间不能穿过 $y=x-1$ ,这也是一个小规模的问题,方案数为 $C_{n-i-1}$ 。于是我们可以写出递推式: $C_n=sum_{i=0}^{n-1}C_iC_{n-i-1},C_0=0$ 。
这个递推式的时间复杂度是 $O(n^2)$ ,追求极致效率的出题人一定不会满意。我们能不能找到一个更快的方法?
我们可以试着求一下卡特兰数的通项公式,一步到位,算出方案数。我们发现不穿过 $y=x$ 这条限制很难处理,我们考虑对其进行容斥,那么 $C_n$ 就是所有路径条数(这是 $ binom{2n}{n}$ )减去穿过 $y=x$ 的路径条数。但是穿过 $y=x$ 的路径的条数看上去依然不是很好求!怎么求呢?我们发现穿过 $y=x$ 的路径必定有一个点在 $y=x+1$ 上,突发奇想,我们找到第一个这样的点,把它后面的路径翻转。
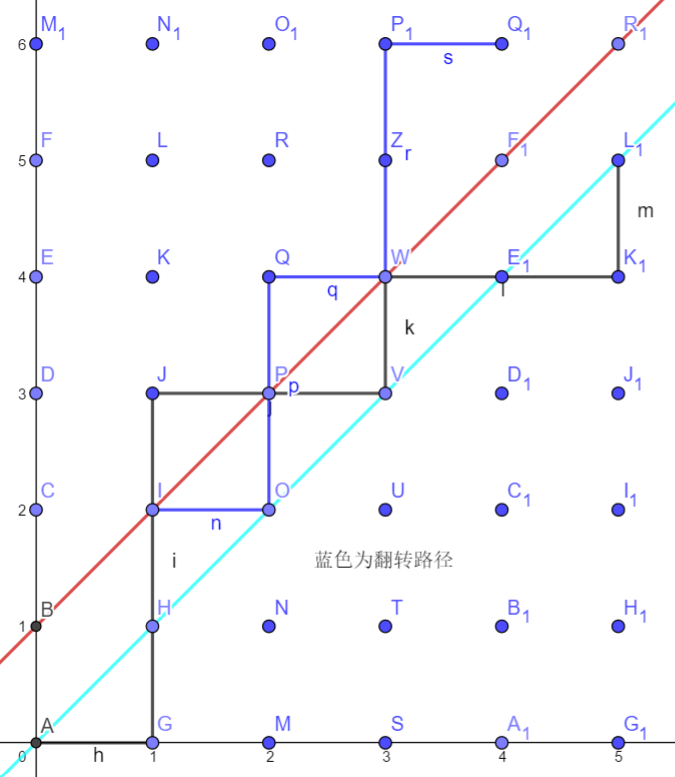
可以看出,翻转后终点变为了 $(n-1,n+1)$ ,并且我们惊奇地发现,翻转前的一条不合法路径刚好对应一条翻转后的路径,而翻转后的一条路径也刚好对应一条翻转前的路径。所以,翻转前后的路径一一对应,也就是说翻转前的不合法路径条数等于翻转后的路径条数,也即 $ binom{2n}{n-1}$ 。由此我们可以得到, $C_n= binom{2n}{n}- binom{2n}{n-1}=frac{1}{n+1} binom{2n}{n}$ ,这个通项公式大大方便了我们的计算。
事实上,根据通项公式我们还可以得到卡特兰数的一个几乎无用的 $O(n)$ 通项公式和一个虽然 $O(n)$ 但不直观、计算价值不大的递推式。但出题人可能会把它们从尘封的角落里取出,所以这值得一提。
$$C_n=dfrac{1}{n+1}sum_{i=0}^ndbinom{n}{i}^2$$
$$C_n=dfrac{4n-2}{n+1}C_{n-1},C_0=1$$
第二个补充例子是二叉树计数:你要数出 $n$ 个点的无标号有根二叉树的棵数。
我们直接设 $f_n$ 为 $n$ 个点的二叉树的棵数,枚举其左子树的大小进行递推,那么 $f_0=1,f_n=sum_{i=0}^{n-1}f_if_{n-i-1}$ 它与卡特兰数初项相同,递推方式也相同,因此它就是卡特兰数,也即 $f_n=C_n$ , $n$ 个点的二叉树棵数为 $C_n$ ,这样你就无需一棵一棵地数了!
总结一下两个例题,对卡特兰数的理解大体有两种,一种是二维平面上迷路的理解,另一种是划分物体的理解(例如用根将二叉树划分为左右子树),两种理解都很有意义。另外,求通项公式时构造了一个翻折变换,使得原、新路径一一对应从而方便计数,也十分精彩。希望大家能熟练掌握这些内容。
下接:卡特兰数题目讲解