参考博客容斥原理(翻译)
容斥原理是组合数学方法,可以求解集合、复合事件的概率等。
原理描述:
计算几个集合并集的大小,先计算出所有单个集合的大小,减去所有两个集合相交的部分,加上三个集合相交的部分,再减去四个集合相交的部分,以此类推,一直计算到所有集合相交的部分 。
维恩图:
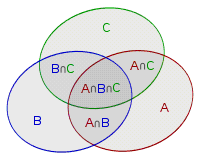
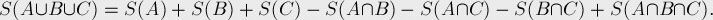
概率论:
事件Ai(i=1,...,n),P(Ai)为对应事件发生的概率。至少一个事件发生的概率:
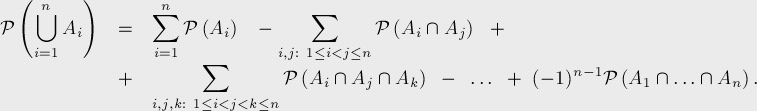
容斥原理的证明:
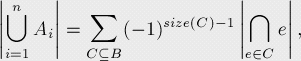
B为Ai的集合。
假设某个任意元素在k个Ai集合中(k>=1),证明这个元素只被加了一次:
size(C)=1,该元素被加k次
size(C)=2,该元素被加(-1)^(2-1)* C(k,2)次
size(C)=3,该元素被加(-1)^(3-1)* C(k,3)次
...
size(C)=k,该元素被加(-1)^(k-1)* C(k,k)次
size(C)>k,该元素被加0次
计算总次数:
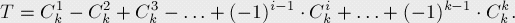
codeforces gym 101350G
题意:给出n*m的矩形,其中有k个炸弹(k<20),求出不包含炸弹的矩形的总个数。
思路:炸弹个数k很小,可以运用容斥,处理恰包含i(i=1,2,...,k)个炸弹(枚举任意的i个炸弹,处理恰包含这i个炸弹的最小的矩形,公式处理。)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=55;
#define sa(x) scanf("%d",&x)
#define pr(x) printf("%d
",x)
#define de(x) cout<<#x<<" = "<<x<<endl;
#define pb push_back
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
//--------------------------------------//
ll x[N],y[N];
ll n,m;
int k;
ll solve() {
ll x1,x2,y1,y2,ans=0;
for(int i=1;i<(1<<k);++i) {
ll bits=0;
ll res=1ll;
for(int j=0;j<k;++j) {
if((1<<j)&i) {
if(!bits) x1=x2=x[j],y1=y2=y[j];
else {
x1=min(x1,x[j]);
y1=min(y1,y[j]);
x2=max(x2,x[j]);
y2=max(y2,y[j]);
}
++bits;
}
}
ll t=x1*(n-x2+1)*y1*(m-y2+1);
if(bits&1) ans+=t;
else ans-=t;
}
return ans;
}
int main() {
int T;sa(T);
while(T--) {
scanf("%I64d%I64d%d",&n,&m,&k);
for(int i=0;i<k;++i) scanf("%I64d%I64d",&x[i],&y[i]);
ll ans=(1ll+n)*n*(1ll+m)*m/4ll-solve();
printf("%I64d
",ans);
}
return 0;
}
hdu 4135
题意:区间[a,b]内与n互质的数的个数。
思路:将n质因数分解。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<iostream>
#include<algorithm>
#include<map>
#include<queue>
#include<set>
#include<vector>
using namespace std;
typedef long long ll;
const int N=1000005;
#define de(x) cout<<#x<<" = "<<x<<endl;
#define pb push_back
#define fi first
#define se second
#define mp make_pair
#define pii pair<int,int>
//--------------------------------------//
ll p[N];
int main() {
int T,cas=0; scanf("%d",&T);
ll a,b,r,ans1,ans2;
while(T--) {
scanf("%I64d%I64d%I64d",&a,&b,&r);
int pcnt=0;
ans1=ans2=0;
--a;
for(ll i=2;i*i<=r;++i) {//对r质因数分解
if(r%i==0) {
p[pcnt++]=i;
while(r%i==0) r/=i;
}
}
if(r>1) p[pcnt++]=r;
for(int i=1;i<(1<<pcnt);++i) {
ll mul=1;
ll bits=0;
for(int j=0;j<pcnt;++j) {
if(i&(1<<j)) {
mul*=p[j];
bits+=1ll;
}
}
if(bits&1) ans1+=a/mul,ans2+=b/mul;
else ans1-=a/mul,ans2-=b/mul;
}
ll ans=b-a+ans1-ans2;
printf("Case #%d: %I64d
",++cas,ans);
}
return 0;
}