排序算法稳定性的定义与意义
排序算法稳定性的定义:
排序算法的稳定性是指:排序前两个相等的数据其在序列中的先后位置顺序与排序后它们两个先后位置顺序相同。
具体简单来讲,如果A[i] = A[j],A[i] 原来在 A[j] 位置前,排序后 A[i] 仍然是在 A[j] 位置前,那么这就是稳定排序。
下面我们分析一下排序算法稳定性的意义:
(1)如果排序算法是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所利用。
基数排序就是这样,先按低位排序,逐次按高位排序,那么,低位相同的数据元素其先后位置顺序即使在高位也相同时是不会改变的。
(2)学习排序原理时,可能编的程序里面要排序的元素都是简单类型,实际上真正应用时,可能是对一个复杂类型(自定义类型)的数组排序,而排序的键值仅仅只是这个元素中的一个属性,对于一个简单类型,数字值就是其全部意义,即使交换了也看不出什么不同。
但是,对于复杂类型,交换的话可能就会使原本不应该交换的元素交换了。比如:一个“学生”数组,欲按照年龄排序,“学生”这个对象不仅含有“年龄”,还有其它很多属性。
假使原数组是把学号作为主键由小到大进行的数据整理。而稳定的排序会保证比较时,如果两个学生年龄相同,一定不会交换。
那也就意味着尽管是对“年龄”进行了排序,但是学号顺序仍然是由小到大的要求。
稳定排序算法应用场景:
假设某银行只有一个窗口为客户服务,银行服务规则根据客户VIP等级和到场时间进行服务,若VIP等级一样,将按照到场时间先后进行服务。现如今,先后来了很多客户,有相同VIP等级的客户。对系统中的服务记录数据,只按照VIP等级进行稳定排序,就可以服务客户。
快速排序算法原理
快速排序的原理:是给基准数据找其正确索引位置的过程
快速排序常用术语:基准数,标志,指针,游标(后三个术语具有相同含义)
下面结合图例来理解快速排序
1.最开始选定的基准数据为数组第一个元素8,则首先用一个临时变量去存储基准数据,即tmp=8;然后分别从数组的两端扫描数组,设两个指示标志:左标志left=0指向起始位置,右标志right=4指向数组末尾
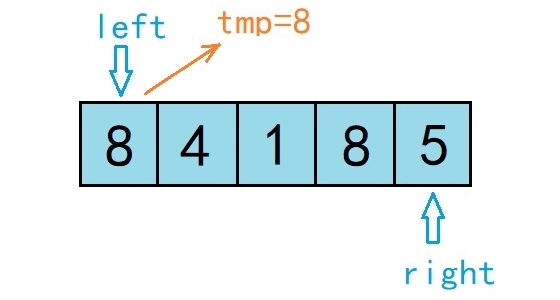
2.从数组右边开始,right=4。如果扫描到的值大于基准数据就让right减1,如果发现有元素比该基准数据的值小(如上图中5<=tmp),就将right=4位置的值赋值给left=0位置,。结果如下图:
然后left++,因为left=0处的值已经小于基准数,所以接下来从left+1处继续执行算法。

3.从左往右扫描,如果扫描到的值小于基准数据就让left加1,如果发现有元素大于基准数据的值,就将left位置的值赋值给right位置的值。左移标志继续向右动最终left=right=4,结果如下:
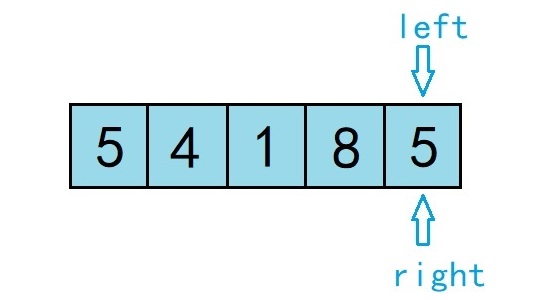
4.left=right,基准数据的正确位置已找到,接下来将tmp中保存在基准数据存放在正确索引位置(也就是arr[left] = arr[4] = tmp = 8),第一个基准元素完成定位,如图所示:
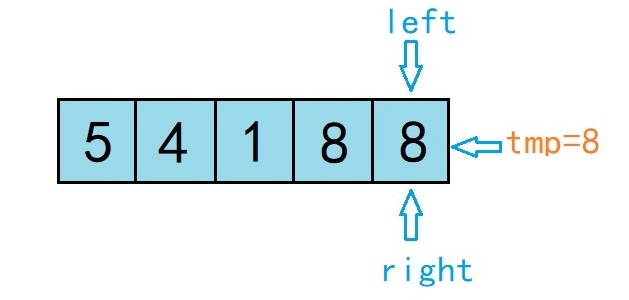
5.递归调用快排函数,重复执行1,2,3,4步骤,直到递归结束,完成排序。
PS:从上述1-4步骤看出,起始数组元素序列A[1] = A[4] = 8,A[1] 顺序在A[4] 前,排序后, A[1] 顺序在A[4] 后,由此可见快速排序不是稳定排序。
| 排序前 | A[1] | A[2] | A[3] | A[4] | A[5] |
| 8 | 4 | 1 | 8 | 5 | |
| 排序后 | A[3] | A[2] | A[5] | A[4] | A[1] |
| 1 | 4 | 5 | 8 | 8 |
快速排序算法稳定性及时间复杂度
快速排序算法稳定性:
快速排序、选择排序、希尔排序、堆排序是不稳定的排序算法,
冒泡排序、插入排序、归并排序和基数排序是稳定的排序算法。
快速排序时间复杂度:
平均情况:O(nlog2n)、最坏情况:O(n2)、最好情况:O(nlog2n)

快速排序C语言代码

1 #include <stdio.h>
2 #include <stdlib.h>
3 //快排核心算法
4 void quickSort(int arr[], int left, int right){
5 //递归结束条件:如果[left, right]区间只剩一个或没有数了,那么函数直接返回
6 if(left < right){
7 //保存左右标志的值,用于递归调用
8 int l = left, r = right;
9 //选取最左端的数作为基准数,用临时变量tmp将基数暂时保存
10 int tmp = arr[left];
11 while(left < right){
12 //向左移动右标志,直到右标志位数值小于基准数
13 while(tmp <= arr[right] && left < right)
14 right--;
15 //右标志位数已经小于基准数,与左标志位交换
16 if(left < right)
17 arr[left++] = arr[right];
18
19 //向右移动左标志,直到左标志位数值大于基准数
20 while(tmp >= arr[left] && left < right)
21 left++;
22 //左标志位数已经大于基准数,与右标志位交换
23 if(left < right)
24 arr[right--] = arr[left];
25 }
26 //将基准数放在正确索引位置中
27 //正确索引位置是指,数组升序排好,基准数所在的位置
28 arr[left] = tmp;
29 //递归调用
30 quickSort(arr, l, left - 1);
31 quickSort(arr, left + 1, r);
32 }
33 }
34
35 //此函数用于打印数组,和排序算法无关。
36 void showArray(int arr[], int arrLength){
37 int i;
38 for(i = 0; i < arrLength; i++){
39 printf("%d ", arr[i]);
40 }
41 printf("
");
42 }
43
44 int main()
45 {
46 //待排序数组
47 int arr[] = {34,6,8,27,65,68,19,40,99,0};
48 //数组长度
49 int arrLength = sizeof(arr)/sizeof(arr[0]);
50
51 printf("排序前:
");
52 showArray(arr, arrLength);
53
54 //调用快排函数,对数组进行排序
55 quickSort(arr, 0, arrLength - 1);
56
57 printf("排序后:
");
58 showArray(arr, arrLength);
59
60 return 0;
61 }
