题目:https://www.acwing.com/problem/content/227/
题意:给你n,k,m,然后输入一个n阶矩阵A,让你求 S=A+A^2+A^3.+......+A^k
思路:首先因为A是矩阵,我们k的范围很大,那么很明显看出A^k可以用矩阵快速幂来计算,但是这样我们只能算出其中一项,还是有k项,那么我们怎么计算和呢
我们可以看出前一项和后一项是有关联的,就是乘了一个A,我们怎么利用前面计算的结果呢,On遍历肯定不行,既然我们用到了遍历,那么优化我们很容易想到二分
假设我们 A+A^2+A^3+A^4+A^5+A^6
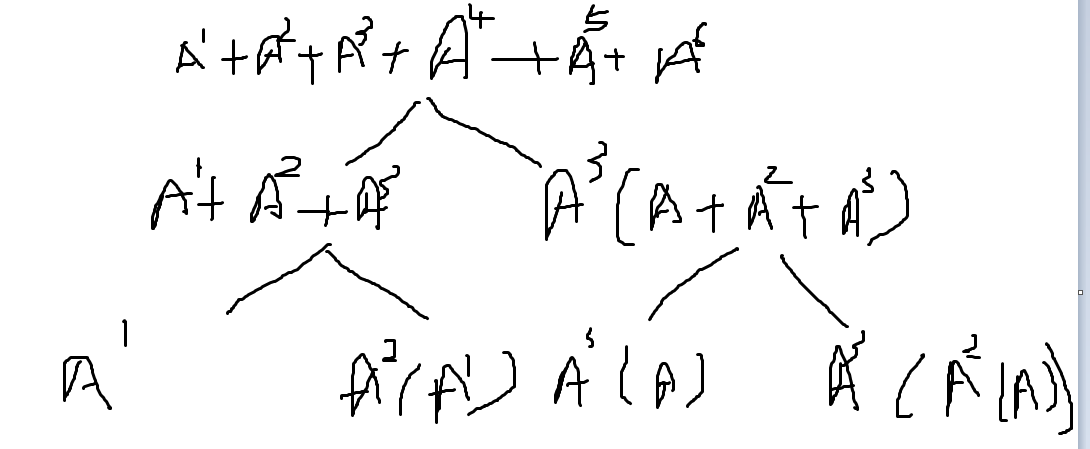
那么可以利用类似分治的方法,一直这样二分递归下去,然后我们自底向上,以左子树推出又子树,这样就能得到最终的答案
#include<bits/stdc++.h> using namespace std; #define MAXN 35 typedef long long ll; int n,mod; struct mat { ll m[MAXN][MAXN];//矩阵结构体 }unit;//unit为单位矩阵,即主对角线全部为1,这样任何矩阵与单位矩阵相乘都为它本身 mat msub(mat a,mat b)//矩阵相乘函数 { mat ret; ll x; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { x=0; for(int k=0;k<n;k++) { x+=((a.m[i][k]*b.m[k][j])%mod);//取余 } ret.m[i][j]=x%mod;//取余 } } return ret; } mat add(mat a,mat b)//矩阵相乘函数 { mat ret; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { ret.m[i][j]=(a.m[i][j]+b.m[i][j])%mod; } } return ret; } void init_unit()//初始化单位矩阵 { for(int i=0;i<MAXN;i++) { unit.m[i][i]=1; } } mat qpow(mat a,ll x)//快速幂 { mat ans=unit; while(x) { if(x&1) ans=msub(ans,a); a=msub(a,a); x>>=1; } return ans; } mat sum(mat a,ll k){ if(k==1) return a; mat w=sum(a,k/2); if(k%2){ mat ans=qpow(a,k/2+1); ans=add(ans,msub(ans,w)); return add(w,ans); } else{ mat ans=qpow(a,k/2); return add(w,msub(ans,w)); } } int main() { ll x; init_unit(); cin>>n>>x>>mod; mat a,ans; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { cin>>a.m[i][j]; } } ans=sum(a,x); for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(j!=n-1) cout<<ans.m[i][j]<<" "; else cout<<ans.m[i][j]<<endl; } } return 0; }