题目:https://vjudge.net/contest/307753#problem/E
题意:给你一颗树,树上每个点都有个权值,现在问你是否存在 一条路径的乘积 mod 1e6+3 等于 k的路径,如果有找到字典序最小的方案
思路,树上路径~点分治 我们能知道每条路径的值,现在我们可以转化的问题是,怎么找一条路径等于K,和两条路径的乘积等于K, 首先第一种很明显就是判断相不相等即可,第二种的话,我们知道所有路径,我们怎么找到O(n)找到两个呢,我们用个数组存下所有是否出现过,然后,其实就是一个简单的小学问题,我们枚举每个距离的时候相当于 x,y,z已经知道 x,z了,式子是x*y=z,我们就只要判断z/x是否在标记数组中出现过即可,又因为这个有mod ,所以我们只能去乘z的逆元,这个时间卡的有点紧,我加了输入挂,和预处理逆元,map标记都不能用,只能用普通标记数组。
然后还有一个问题,你是否能和之前那样直接求出来所有的距离,答案是否定的,因为你直接去遍历数组标记,数组中的路径还含有两个都是同一子树的情况,这种时候是不能加入标记数组的,但是怎么避免呢,这里用到一个巧妙地方法,我们直接在计算所有路径到重心的距离的时候去更新答案,因为我们只有得到一个子树所有答案的时候才会存入标记数组,这样就避免一个子树的路径发生冲突的情况。最后我们再清空掉我们当前重心存入的答案。
还有更新答案的时候要注意的是,我们前面子树都保存的是点到重心的路径值,这里我们就不能也用点到重心的值了,因为就会多乘了一个重心节点的值,看下图
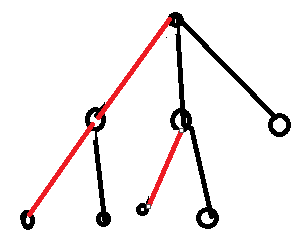
上面就是两条红色路径相乘就是两个路径合并起来了,主要还是因为这是点权,覆盖路径上所有点的点

#pragma comment(linker,"/STACK:102400000,102400000") #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<iostream> #include<vector> #include<map> #define maxn 1000005 #define mod 1000003 #define MAX 0x3f3f3f using namespace std; typedef long long ll; struct edge{ int to,next; }e1[2*maxn]; ll da; ll flag[maxn]; //vector<ll> mp[maxn];//存下图 bool vis[maxn];//标记曾经使用过的重心 ll maxsize[maxn],dis[maxn],d[maxn],last[maxn];//maxsize 当前节点的最大子树 ll siz[maxn],e[maxn],e2[maxn],id[maxn],wd[maxn],inv[maxn];// dis 到重心的距离 d 出现过的距离 ll n,m,rt,sum,qe,qe2,ans1,ans2,cnt; // siz 当前节点的子树个数 e 出现的距离 rt代表当前重心 inline ll read() { ll x=0;char ch=getchar(); while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x; } void insert(int u,int v) { e1[++cnt].to=v;e1[cnt].next=last[u];last[u]=cnt; e1[++cnt].to=u;e1[cnt].next=last[v];last[v]=cnt; } void find(ll x,ll f){//找出重心 siz[x]=1; maxsize[x]=0; for(int i=last[x];i;i=e1[i].next){ ll q=e1[i].to; if(q==f||vis[q]) continue;//vis数组标记曾经使用过的重心 find(q,x); siz[x]+=siz[q]; maxsize[x]=max(maxsize[x],siz[q]); } maxsize[x]=max(maxsize[x],sum-siz[x]);//节点总数减去当前的子树数=以当前节点为根的父亲点子树数 if(maxsize[x]<maxsize[rt]){ rt=x; } } void query(ll x,ll y){ if(x>y) swap(x,y); if(x<ans1||(x==ans1&&y<ans2)){ ans1=x; ans2=y; } } void get_dis(ll x,ll f,ll len,ll root){ ll t=len%mod; if(t==m){//判断当前路径是否直接等于m query(root,x); } t=t*inv[wd[root]]%mod;//除去重心到子树那段距离,原因就是上述图 ll t1=inv[t]*m%mod; e[++qe]=len%mod; e2[++qe2]=len%mod;//后面清空标记 id[qe]=x; if(flag[t1]){//看是否另一条路径存在 query(flag[t1],x); } for(int i=last[x];i;i=e1[i].next){ ll q=e1[i].to; if(q==f||vis[q]) continue; // dis[q]=(dis[x]*len)%mod; get_dis(q,x,(len*wd[q])%mod,root); } } void divide(ll x){ //solve(x,wd[x]); qe2=0; vis[x]=1; for(int i=last[x];i;i=e1[i].next){ ll q=e1[i].to; qe=0; get_dis(q,x,wd[x]%mod*wd[q]%mod,x); for(int i=1;i<=qe;i++){//记录当前的子树所有的距离 if(flag[e[i]]==0) flag[e[i]]=id[i]; else flag[e[i]]=min(flag[e[i]],id[i]); } } for(int i=1;i<=qe2;i++){//清空标记 flag[e2[i]]=0; } for(int i=last[x];i;i=e1[i].next){ ll q=e1[i].to; if(vis[q]) continue; sum=siz[q]; rt=0; maxsize[rt]=MAX; find(q,x); divide(rt); } } void init(){ for(int i=0;i<=n;i++) last[i]=0; for(int i=0;i<=n;i++) vis[i]=0; for(int i=0;i<=n;i++) flag[i]=0; } void pre(){ cnt=0; inv[1] = inv[0] = 1; for (ll i = 2; i < maxn; i++) inv[i] = (mod - mod / i)*inv[mod%i] % mod; } int main(){ pre(); while(scanf("%lld%lld",&n,&m)!=EOF) { //if(n==0&&m==0) break; ll a,b,c; init(); ans1=MAX;ans2=MAX; for(int i=1;i<=n;i++) wd[i]=read(); for(int i=1;i<n;i++) { int u=read(),v=read(); insert(u,v); } sum=n;//当前节点数 rt=0; maxsize[0]=MAX;//置初值 find(1,0); divide(rt); if(ans1!=MAX&&ans2!=MAX) printf("%lld %lld ",ans1,ans2); else printf("No solution "); } }
