支持向量机（support vector machines, SVM）

支持向量机SVM是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，可将问题化为求解凸二次规划的问题。

• 在线性可分时，在原空间寻找两类样本的最优分类超平面。
• 在线性不可分时，加入松弛变量并通过使用非线性映射将低维输入空间的样本映射到高维空间使其变为线性可分。

决策面方程

如果输入的数据是一个L维空间特征，考虑一个M分类问题，那么分类器将会把这个L维空间的特征点分为M个区域。每个区域显然就属于一个类别，如果输入一个点x落在第i个区域，那么x就属于第i类。分割成这些区域的边界就称为决策面。

二维空间直线方程

• _，

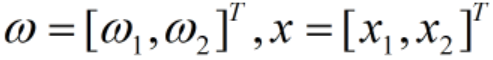
• 向量ω和直线的关系为垂直关系，称ω为直线的法向量。标量γ决定了直线的截距。

超平面方程

• 二维空间的直线方程已经推导完成，将其推广到n为空间，就变成了超平面方程。
• ，

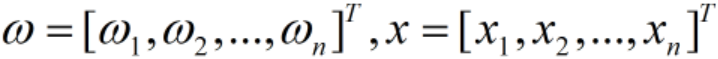
分类间隔方程

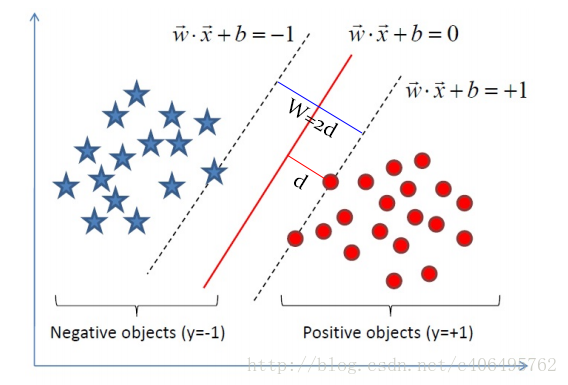
• 在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。
• 虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。
• 而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。

 

• d就是分类间隔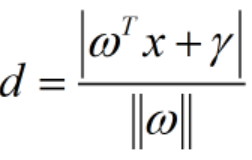，；||ω||表示ω的二范数，求所有元素的平方和，然后再开方，。
• 分类器的好坏的评定依据是分类间隔W=2d的大小，即分类间隔W越大，我们认为这个超平面的分类效果越好。此时，求解超平面的问题就变成了求解分类间隔W最大化的问题。

约束条件

判断超平面是否将样本点正确分类？

怎么在众多的点中选出极限位置的点呢？

• 对于二分类问题：在二维平面上有两种点，我们分别对它们进行标记：
  • 红颜色的圆点标记为1，规定其为正样本；
  • 蓝颜色的五角星标记为-1，规定其为负样本。
• 对每个样本点x_i加上一个类别标签y_i：
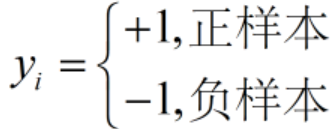
• 如果我们的超平面方程能够完全正确地对上图的样本点进行分类，就会满足下面的方程：
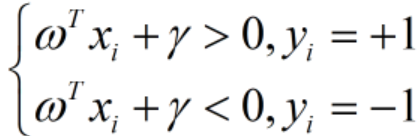
• 如果假设决策面正好处于间隔区域的中轴线上，并且相应的支持向量对应的样本点到决策面的距离为d，那么公式进一步写成：_。上述公式的解释就是，对于所有分类标签为1的样本点，它们到直线的距离都大于等于d(支持向量上的样本点到超平面的距离)。对于所有分类标签为-1的样本点，它们到直线的距离都小于等于d。
• 公式两边都除以d，就可以得到：，。
• 因为||w||和d都是标量。所上述公式的两个矢量，依然描述一条直线的法向量和截距。
• 因此，“对于存在分类间隔的两类样本点，我们一定可以找到一些超平面，使其对于所有的样本点均满足条件：
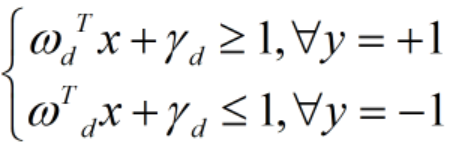
• 设置分类标签为+1和-1，则得到约束方程：

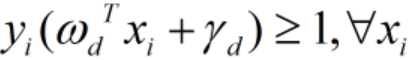
参考：https://blog.csdn.net/c406495762/article/details/78072313#2-smo%E7%AE%97%E6%B3%95

线性可分问题

使用支持向量上的样本点求解分类间隔d的最大化的问题，此时满足：，所以求解d的最大值，可以转换为求解||w||的最小值。

，这里n是样本点的总个数，上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题。

拉格朗日优化

• 将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
• 使用拉格朗日对偶性，将不易求解的优化问题转化为易求解的优化

1.凸二次规划的拉格朗日函数

，α_i是拉格朗日乘子，α_i大于等于0，是构造新目标函数时引入的系数变量，自行设置。(b=γ)

令：。当样本点在可行解区域内时：；反之，样本点在可行解区域外时：

得到新的目标函数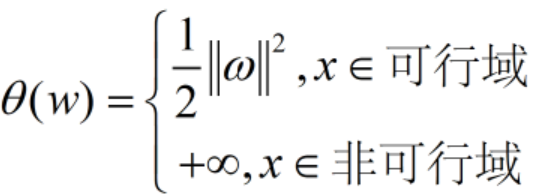：，因此需要求取新目标函数的最小值

2.拉格朗日对偶性优化求解

参考：https://zhuanlan.zhihu.com/p/38182879

按照原问题p^*求解：首先就要求解的参数w和b的方程，而α_i又是不等式约束，难以求解。所以，使用拉格朗日函数对偶性，将最小和最大的位置交换一下，这样就变成了：

使得d^*=p^*的条件：

• 首先必须满足这个优化问题是凸优化问题。
• 其次，需要满足KKT条件。

对偶转换后求解：

• 求解内侧最小值：首先固定α，要让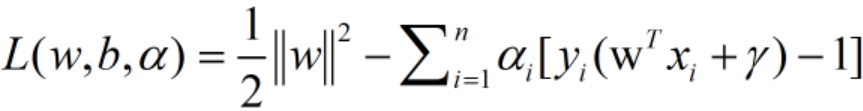关于w和b最小化，分别对w和b偏导数，令其等于0，即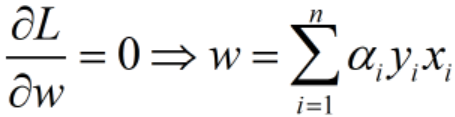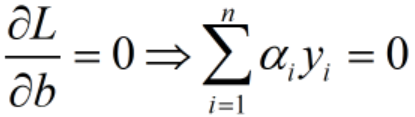：_,。再带入L(w,b,α)得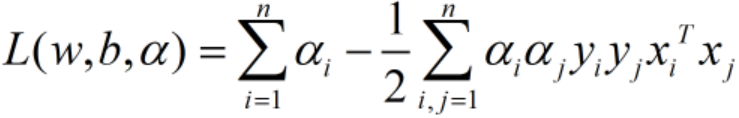：，此时式子中只有α一个变量。  
• 求外侧最大值：对于下列形式，可以是使用序列最小优化（SMO）算法。我们通过这个优化算法能得到α，再根据α，求解出w和b，进而求得超平面。

参考：https://blog.csdn.net/LittleEmperor/article/details/105057670?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param

SMO算法

• 不断地将原二次规划问题分解为只有两个变量的二次规划子问题，并对子问题进行解析求解，直到所有变量满足KKT条件为止。
• SMO算法的目标是求出一系列α和b，一旦求出了这些α，就很容易计算出权重向量w并得到分隔超平面。
• SMO算法的工作原理是：每次循环中选择两个α进行优化处理。一旦找到了一对合适的α，那么就增大其中一个同时减小另一个。这里所谓的"合适"就是指两个α必须符合以下两个条件，条件之一就是两个α必须要在间隔边界之外，而且第二个条件则是这两个α还没有进进行过区间化处理或者不在边界上。

线性不可分问题

• 线性不可分即指部分训练样本不能满足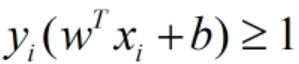的条件。解决方法：加入松弛变量，允许一些点到分类平面距离不能满足原先的要求。具体约束条件中增加一个松弛参数ε_i≥0，变成 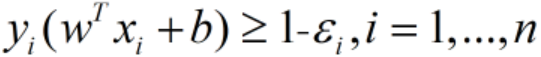：。当ε_i足够大时，训练点就可以满足以上条件。
• 虽然得到的分类间隔越大越好，但也需要避免ε_i取太大的值。所以在目标函数中加入惩罚项，得到优化问题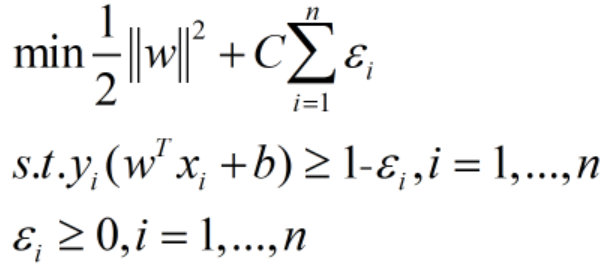：，其中ε∈Rⁿ，C是一个惩罚参数。目标函数意味着既要最小化||w||²（即最大化间隔），又要最小化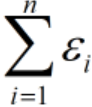（即约束条件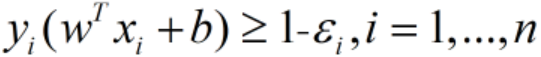的破坏程度，参数C体现了两者总体的一个权衡。

SVM的非线性映射问题

• 非线性问题需要通过非线性交换转化为某个高维空间中的线性问题，在新的高维空间内求最优分类超平面。非线性变换的方式就是利用核函数。
• 核函数的充要条件是：任何半正定对称函数都可作为核函数
• 常用的核函数：多项式核，高斯核额，余弦相似核，卡方核