第16课——递归的应用实战二—八皇后问题

递归与回溯

8皇后问题：

在一个8*8棋盘上，有8个皇后，每个皇后占一格；要求两个皇后不能处在同一行、同一列或同一对角线上。

 

找放置的位置，方向很重要，当从第一行开始，放置皇后的位置后，第二行放置时要考虑上一行的放置。

 

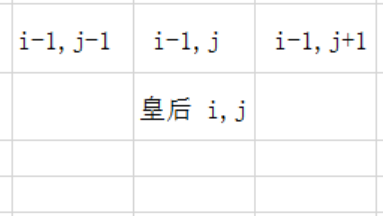
即3个方向为（-1，-1），（-1, 0），（-1，1）

#include <stdio.h>

#define N 8

typedef struct _tag_Pos
{
    int ios;
    int jos;
} Pos;

static char board[N+2][N+2];
static Pos pos[] = { {-1, -1}, {-1, 0}, {-1, 1} }; //定义方向
static int count = 0;


void init()
{
    int i = 0;
    int j = 0;
    
    for(i=0; i<N+2; i++)
    {
        board[0][i] = '#';    //上边框
        board[N+1][i] = '#';  //下边框
        board[i][0] = '#';    //左边框
        board[i][N+1] = '#';  //右边框
    }
    
    for(i=1; i<=N; i++)
    {
        for(j=1; j<=N; j++)
        {            
            //board[i][j] = j + '0 ';
            board[i][j] = ' ';
        }
    }
}

void display()
{
    int i = 0;
    int j = 1;
    
    for(i=0; i<N+2; i++)
    {
        for(j=0; j<N+2; j++)
        {
            printf("%c", board[i][j]);  //打印棋盘位置
        }        
        printf("
");
    }
}

int check(int i, int j)
{
    int ret = 1;
    int p = 0;
    
    for(p=0; p<3; p++) //找3个方向
    {
        int ni = i;
        int nj = j;
        
        while( ret && (board[ni][nj] != '#') ) //当（ni,nj）位置没碰到边界
        {
            ni = ni + pos[p].ios;  //执行3个方向上的++
            nj = nj + pos[p].jos;
            
            ret = ret && (board[ni][nj] != '*'); //当3个方向位置都没有皇后，则返回1.
                                                //否则返回0；
        }
    }
    
    return ret;
}

void find(int i)
{
    int j = 0;
    
    if( i > N )  //如果i>N ，说明已经把N行找完，故8皇后已经放好
    {
        count++;   //计数种数
        
        printf("Solution: %d
", count);
        
        display();  //打印放法
        
        getchar(); //执行暂停，等到有字符输入就继续
    }
    else
    {
        for(j=1; j<=N; j++)
        {
            if( check(i, j) )  //如果（i,j）位置可以放皇后，则返回1
            {
                board[i][j] = '*';   //放置皇后
                
                find(i+1);   //继续找下一行（i+1)行
                
                board[i][j] = ' ';  //若下一行没找到可以放置的点，则可能上一行的皇后放错了，
                                    //故回溯到i行，并把上一行已经放置的（i,j）位置清除。
                                    //继续在上一次的j位置往后找可以放置皇后的位置。
            }
        }
    }
}

int main()
{
    init();
    find(1); //从第一行开始执行
    
    return 0;
}

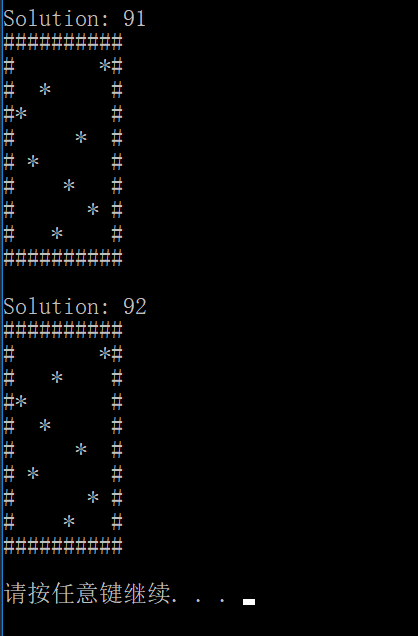
8皇后共有92种。

 用数字遍历棋盘

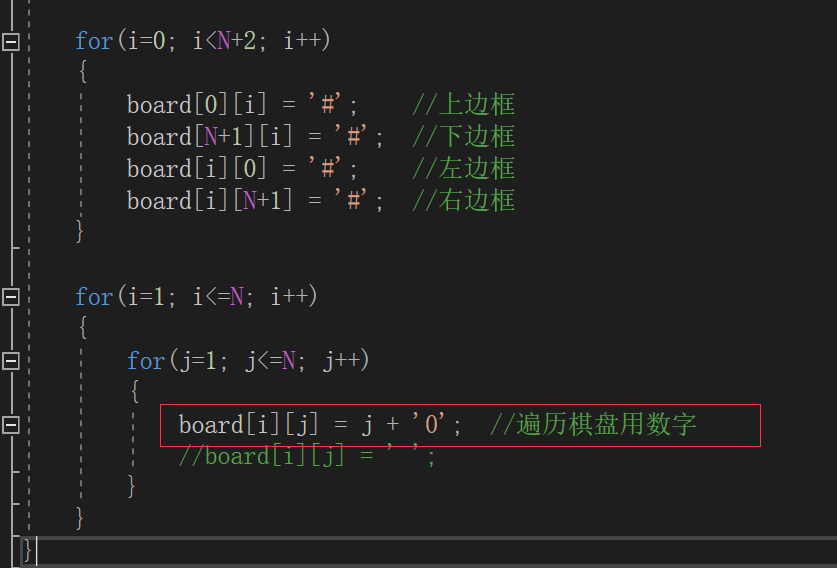
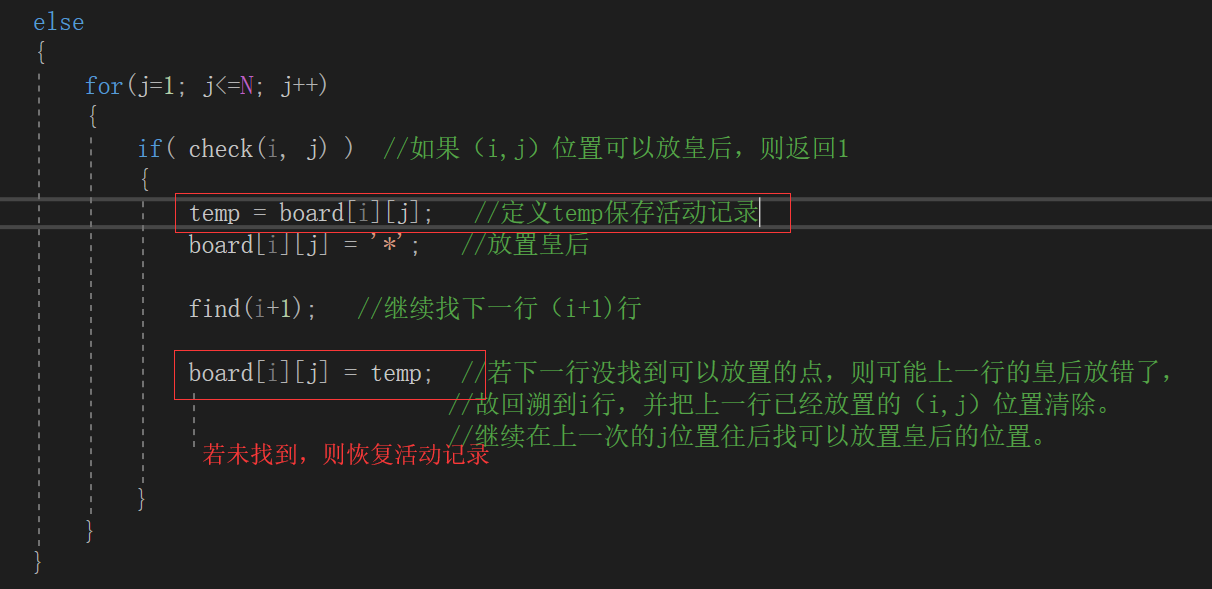
小结：

* 回溯算法是递归应用的重要场合

* 利用函数调用的活动对象可以保持回溯算法中重要的变量信息

递归是回溯算法的重要实现方式！！