P2458 [SDOI2006]保安站岗

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入格式：

 

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个通道端点的信息，依次为：该结点标号i（0<i<=n），在该结点安置保安所需的经费k（<=10000），该边的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1，r2，...，rm。

对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且标号不重复。

 

输出格式：

 

最少的经费。

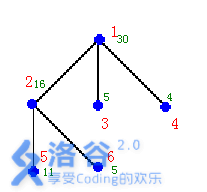
solution

一道树形DP题，难点在于如何设计状态，考虑到一个点有三种情况，由它的父节点看守，或子节点看守，或者自己花费cost[i]的代价看守。

于是我们用DP[i][0]表示第i个点由父节点看守时的最小代价,用DP[i][1]表示自己看守,DP[i][2]表示由子节点看守

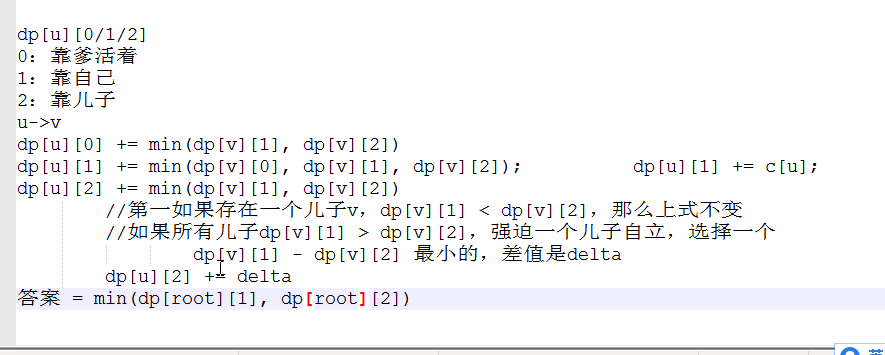
以下就是对上面第三个方程的实现

s=min(s,DP[ev][1]-min(DP[ev][1],DP[ev][2])); 

当子节点自立的代价更小时，很明显最小值是0，也就是说这个子节点一定是自立更优的，DP[u][2]就不需要再更新

否则需要找一个差值最小的强迫他自立，才能满足u由儿子养。

下面我们来看一下代码实现吧。

注意好DP的具体实现

int s=INF;
    for( int i=head[now];i;i=e[i].nxt)
    {
        int ev=e[i].v;
        if(ev!=father)
        {
            dp(ev,now);
            DP[now][0]+=min(DP[ev][1],DP[ev][2]);
            DP[now][1]+=min(DP[ev][1],min(DP[ev][2],DP[ev][0]));
            DP[now][2]+=min(DP[ev][1],DP[ev][2]);
            s=min(s,DP[ev][1]-min(DP[ev][1],DP[ev][2])); //DP的过程很重要 
        }

    }
    DP[now][2]+=s;
    DP[now][1]+=val[now];//DP的过程很重要 

code

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define il inline 
#define re register
#define maxn 2010
#define INF 0x3f3f3f3f
using namespace std;
int y,fa[maxn],root;
int DP[maxn][5],val[maxn],n,m,k,cnt,head[maxn],x;
struct Edge
{
  int v,nxt;
}e[maxn];
il int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
} 
il void add(int u,int v)
{
    e[++cnt].v=v;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
void pre()
{
//    memset(DP,-INF,sizeof(DP));
    for(re int i=1;i<=n;++i) fa[i]=i;
}
void dp(int now,int father)
{
    int s=INF;
    for( int i=head[now];i;i=e[i].nxt)
    {
        int ev=e[i].v;
        if(ev!=father)
        {
            dp(ev,now);
            DP[now][0]+=min(DP[ev][1],DP[ev][2]);
            DP[now][1]+=min(DP[ev][1],min(DP[ev][2],DP[ev][0]));
            DP[now][2]+=min(DP[ev][1],DP[ev][2]);
            s=min(s,DP[ev][1]-min(DP[ev][1],DP[ev][2])); //DP的过程很重要 
        }

    }
    DP[now][2]+=s;
    DP[now][1]+=val[now];//DP的过程很重要 
}
int main()
{
    n=read();
    pre();
    for(re int i=1;i<=n;++i)
    {
        x=read();
        val[x]=read();
        m=read();
        for(re int j=1;j<=m;++j)
        {
            y=read();
            add(x,y);
            fa[y]=x;
        }
    }
     root=1;
     //memset()
     while(fa[root]!=root) root=fa[root];
     //printf("%d
",root);
     dp(root,0);
     printf("%d
",min(DP[root][1],DP[root][2]));
    return 0;
}